Пространство. Просто пространство

Слово «пространство» настолько часто используется и самоочевидно, что попытка дать ему определение приводит к эталону тавтологии: Пространство — это пространство. С одной стороны формулы тут — термин, которому мы пытаемся определить значение, с другой — собственно значение.

Попытка обратиться к искусственному интеллекту лишь расшифровывает «аксиоматичность» этого, едва ли не самого базового, понятия.

Насколько слово и понятие «пространство» употребительно в сравнении с другими словами и понятиями?

Нейронка нам скажет:

Однако в этом есть смысл.

Успех заключается в понимании, что пространство в самом общем смысле состоит из пространств, более конкретизированных. И теперь тавтология выглядит несколько иначе:

Пространство — это множество пространств.

Оставляя (пока) за скобками культурно-социологические смыслы, сосредоточимся на трёх строчках:
— Пространство физическое (здесь мы купировали «время», см. наш рассказ «Природа времени»)
— Космическое пространство
— Географическое

То есть, нас интересует «пространство» в самом широком смысле, относительно всей нашей вселенной в целом.
Пространство состоит из множества локальных пространств, «территорий», мест. Различные места в пространстве находятся между собой в некоторых отношениях, то есть здесь — на некоторых расстояниях друг от друга.

Пространство — это множество мест, в которых могут находиться объекты относительно других объектов, каждый из которых находится на своем месте пространства ©.

Место в пространстве, локальная область «большого» пространства, элемент множества — отличается от других мест по расстоянию между ними. Расстояние, таким образом, это необходимое свойство пространства, его обязательный атрибут. Благодаря расстоянию мы может различать объекты между собой. Расстояние — это мера отличия одного места (и объекта в нём) от другого места (и объекта в нём).

Если мы некоторым образом выделим одно место среди других (центр), то получим еще одно определение пространства:

Пространство — это множество расстояний от центра.

Это между, прочим, означает, что к выбору начала координат надо подходить ответственно. Хорошо бы, чтобы это место чем-нибудь выделялось среди прочих. Например, планета Земля является самым большим артефактом из твердого вещества в Солнечной системе (и в сколько-нибудь доступной изучению части этой вселенной).

Если мы некоторым образом определим эталон расстояния (выделим, например, еще некоторое место, помимо центра), то его уже можно измерить и сосчитать, и, таким образом, оно существует.

Рассмотрим вопрос расстояний несколько подробнее.

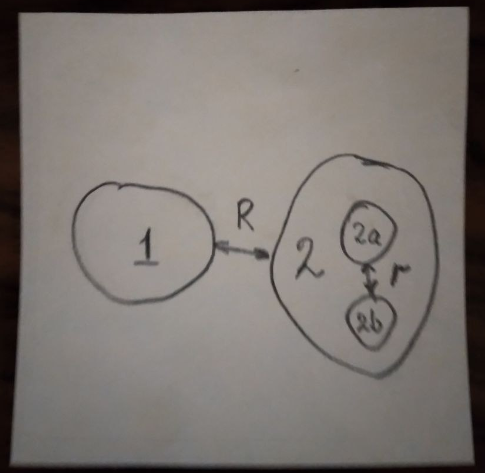
На рисунке плоскость листа представляет «большое» пространство, в котором имеют места два объекта 1 и 2. Между ними есть расстояние R. Второй объект состоит из каких-то своих, входящих в него объектов, 2а и 2b, со своим локальным пространством, и расстоянием между ними r.

Можем ли мы сопоставить (сравнить) R и r? Во-первых, нам надо найти что-то, что будет работать и в подпространстве объекта 2, и в большом пространстве. И во-вторых, нам нужна уверенность в том, что этот механизм в обоих случаях будет работать одинаково.

Это вовсе не покушение на единство мира, материальное, физическое или какое-то еще. Просто законы природы могут оказаться таковы, что единица длины внутри одного подпространства не будет равна самой себе в другом подпространстве или в «большом» пространстве.

Чем занято человечество в вопросе измерения расстояний? Повышением точности, разумеется. А как мы узнали в предыдущем рассказике, достижимая точность ограничена а) тем, какую малость мы возьмём за эталон; б) где-то надо взять гарантии, что копии эталона останутся равными самим себе и эталону.

В настоящее время эталоном длины постановили считать расстояние, которое проходит свет в «пустоте» за 1/299 792 458 долю секунды, а 299 792 458 метров в секунду — это как бы и есть скорость света в пустоте, и сомневаться в этом нельзя. Но к этому вопросу мы имеем твёрдое намерение вернуться, поскольку мы и так уже маргиналы, бояться нам нечего.

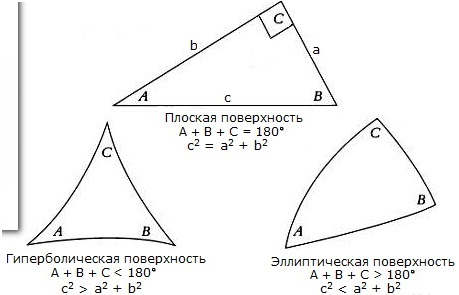
Но проблема есть не только «снизу», но и «сверху» тоже. Речь идёт о кривизне пространства. Не о той зауми, которую развивают «яйцеголовые» в своём якобы научном майнстриме, а о старом добром постулате Евклида о равенстве суммы углов треугольника двум прямым.

Весьма уважаемый мною г-н Лобачевский Николай Иванович как-то заметил, что в отличие от остальных четырёх своих геометрических аксиом, именно о сумме углов Евклид выразился заковыристо:

… и построил геометрию, в которой это не так.

Нет, причин для волнения нет, мироздание неколебимо. Во всех практических нуждах все могут пользоваться веревочкой, с повязанными на ней узлами 5 и 4 и 3.

Но нет никаких гарантий, что наше с вами «большое» пространство — именно Евклидово, и проверить это у нас методов нет. Поэтому человечество пользуется прямыми углами, когда поднимает приборы к небесной сфере.

Но и здесь майнстрим не обошелся без весьма сомнительных предприятий (да, и к этому ещё вернёмся, это будет рассказ о гг Бесселе, Струве и Гендерсоне).

Тема пространства отнюдь не закончена. Есть еще такие вещи, как гравитация и эфир. И если с первым разделаться мы планируем за один небольшой следующий рассказик, то об эфире разговор не на одну толстую книжку. Но мы постараемся справиться покороче. Оставайтесь с нами.