Диаспора

ПРИЛОЖЕНИЯ[127]

Поверхность тора, вложенного в трехмерное пространство, непрерывно искривлена. На первый взгляд кажется невозможным уплощить тор, не превратив меридианы (красные круги) в прямые — тогда все линии широты (синие круги) будут иметь одинаковый радиус. Но тогда топология поверхности изменится, и она станет обычным цилиндром. Однако, вращая каждый меридиан в четвертом пространственном измерении, можно добиться равенства широтных радиусов без ненужного спрямления меридианов. Трехмерная «тень» получившегося объекта выглядит как цилиндр, но различные оттенки передней и задней поверхностей указывают, что на самом деле они не соприкасаются ― в четвертом измерении они разделены.

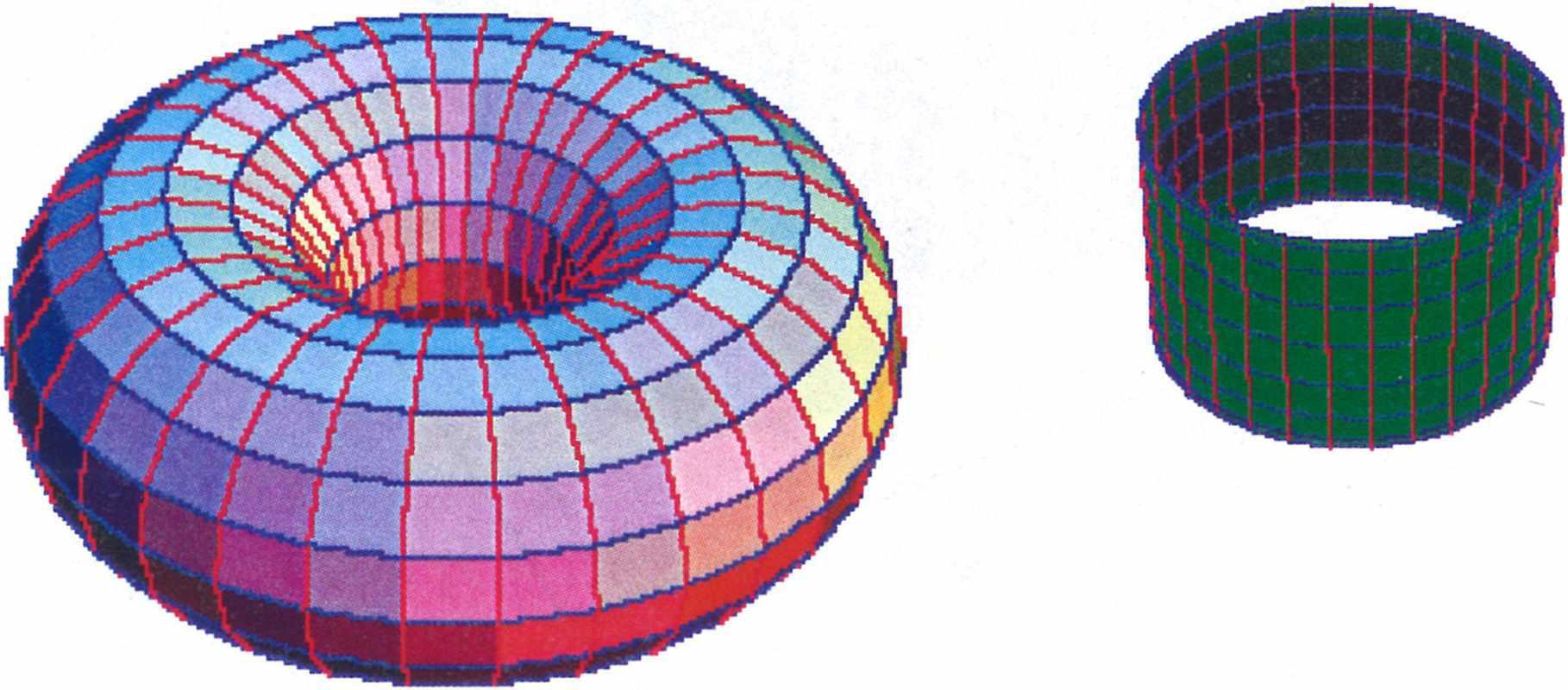
Доказательство.

Стандартный способ вложения тора в три измерения приводит к замене координат

Здесь а, b — соответственно больший и меньший радиусы тора, а углы А, В пробегают значения от 0 до 2π. Выглядит это следующим образом:

Вложение тора в три измерения в координатах (х, у z)

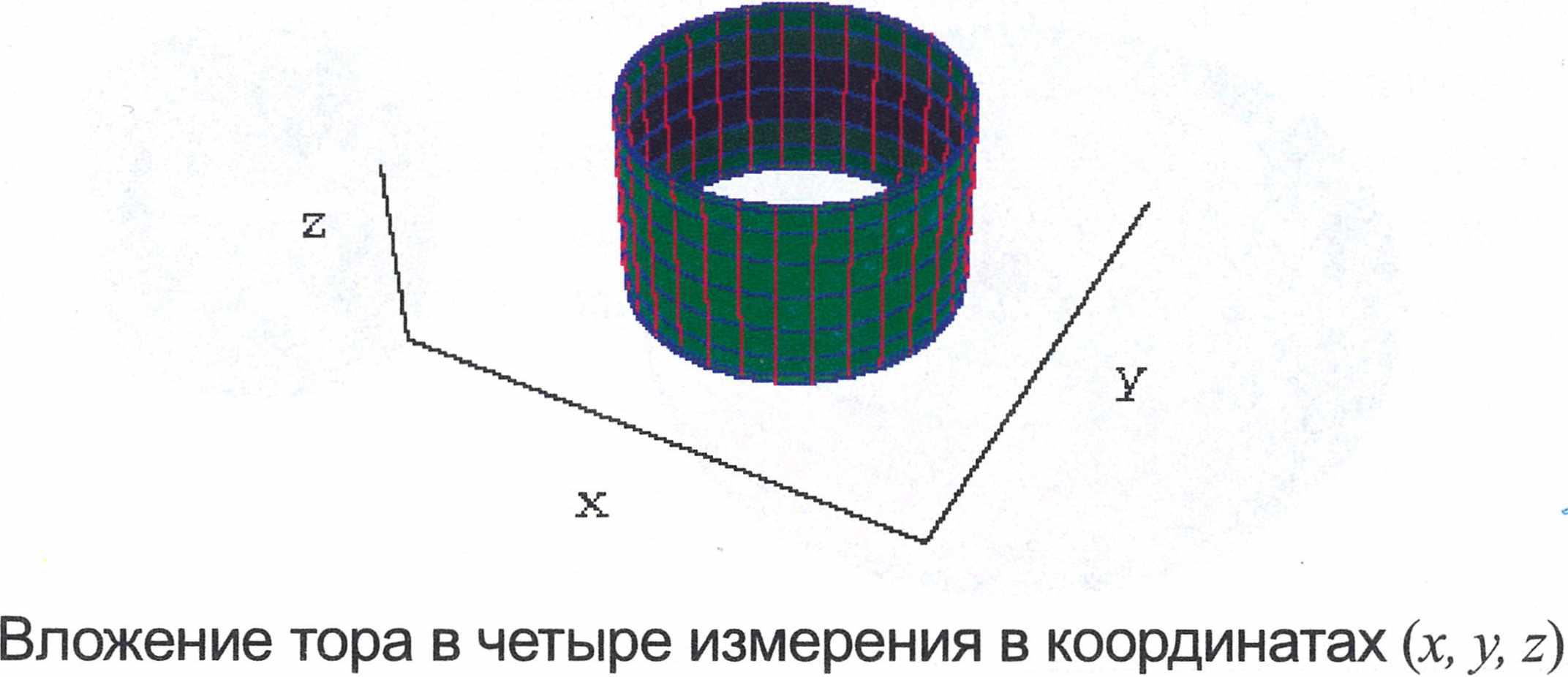
Тор можно вложить и в четыре измерения:

Это новое вложение достигается вращением каждого красного меридиана на 90 градусов в четвертом измерении — расстояние по центральной оси превращается в расстояние по координате w.

Если теперь рассматривать сечение в координатах (х, у, z), меридианы, выглядевшие кругами, вроде бы вырождаются в прямые, но на самом деле это не так. Переходя к координатам (х, у, w) (координата z переведена в цветовую шкалу), видим, что меридианы начинаются с горизонтали и в направлении w выглядят уже вертикальными. В каждом случае круги все еще кажутся прямыми, поскольку четвертая координата показана только цветовой кодировкой.

Вложение тора в три измерения в координатах (х, у, w)

Вложение тора в четыре измерения в координатах (х, у, w)

Сферу тоже нельзя уплощить, вложив ее в любое пространство высшего порядка. Чтобы увидеть, почему это так, мысленно разделите ее на восемь треугольников. Четыре треугольника пересекаются в шести точках, и если бы поверхность, покрытая ими, была плоской, сумма углов вокруг каждой точки равнялась бы 360 градусам, а в сумме набегало бы 360 х 6 = 2160 градусов. Но, учитывая, что сумма углов каждого треугольника должна равняться 180 градусам, восемь треугольников поставляют нам 180 х 8 = 1440 градусов. Одновременно удовлетворить обоим этим условиям невозможно.

Доказательство. Любая поверхность характеризуется числом Эйлера. Если поверхность разбита на многоугольные грани, число Эйлера х наглядно определяется как

Здесь ф — число граней, ε — число ребер, ω — число вершин. Для сферы, разбитой на 8 треугольников, получаем ф = 8, ε = 12, ω = 6, X= 2.

От изменения какого-либо компонента формулы число Эйлера не меняется.

Рассмотрим теперь специальный случай, в котором все треугольники, вымостившие некоторую поверхность, полностью граничат всеми ребрами с соседями. Тогда каждое ребро принадлежит одновременно двум треугольникам. Итак, ε = Зф/2.

Если поверхность плоская, то общая сумма внутренних углов треугольников τ равна τ = 180ф. В то же время τ = З60ω. Отсюда следует, что поверхность может быть уплощена только в том случае, если

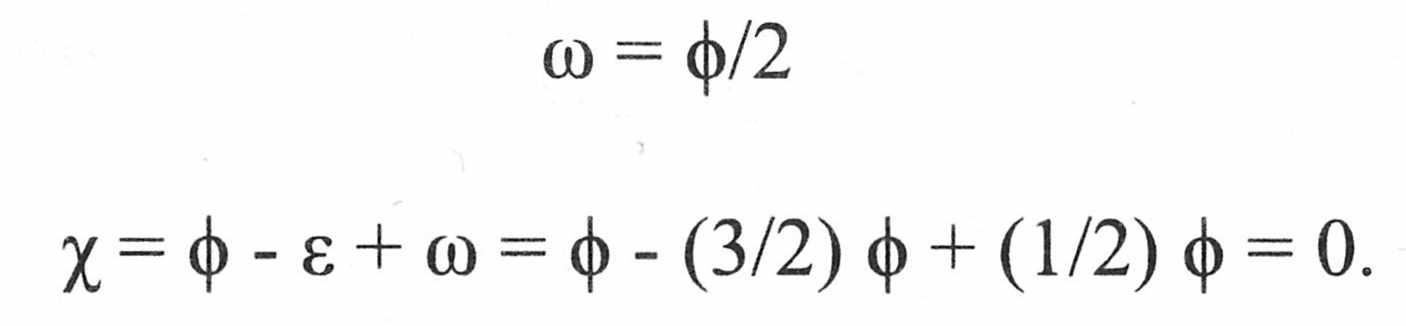
Поскольку для сферы число Эйлера х = 2, уплощить ее невозможно.

На моем сайте можно загрузить интерактивный Java-апплет, иллюстрирующий излучение гравитационных волн двойной системой нейтронных звезд. Для работы с ним ваш браузер должен поддерживать Java. Апплет занимает около 11 Кбайт, так что, если у вас медленный Интернет, загрузка отнимет какое-то время[128].

Следует заметить, что программа использует алгоритмы вычислений, основанные на общей теории относительности в ее современном виде. Эффекты физики вселенной Диаспоры апплет не учитывает.

Период вращения и расстояние между компонентами системы связаны законом Кеплера. Квадрат периода T пропорционален кубу расстояния а:

Здесь M= m₁ + m₂ ― совокупная масса компонентов, a G — гравитационная постоянная. Общая энергия излучения гравитационных волн обратно пропорциональна пятой степени расстояния между звездами:

Здесь μ = (m₁ m₂)/(т₁ + т₂) ― приведенная масса системы. Краткое обоснование соотношения таково: амплитуда гравитационного излучения каждой звезды пропорциональна ее массе т_i и центробежному ускорению ω₂a_i, где а_i — расстояние от центра масс системы, а ω = 2π/Т, а также обратно пропорциональна расстоянию до наблюдателя r. По определению m₁a₁ = m₂a₂ так что звезды генерируют гравитационные импульсы в точности одинаковой амплитуды, а разность фаз между ними составляет 180º. Временная задержка при прохождении звезд не дает волнам скомпенсировать друг друга и поставляет дополнительную разность фаз, пропорциональную (а₁+а₂)ω. Итак, амплитуда волны, регистрируемой удаленным наблюдателем, составляет

A ~ μa²ω³ /r

Мощность излучения пропорциональна квадрату амплитуды. Подставляя вместо ω полученное из закона Кеплера соотношение

ω² ~ M/a³, получаем:

L~ А²r²

L ~ M³μ²Ia⁵

Точные численные коэффициенты при G и c можно найти из анализа размерностей, но все же множитель 32/5 требует учета общей теории относительности. Точное описание движения пробных частиц также выходит за рамки настоящего очерка, но оценить искривление орбиты можно, умножив соотношение для А на Т/2. Получаем　

dx/x ~ μа²ω²/r

Воспользовавшись законом Кеплера и подставляя численные коэффициенты при G и c, имеем

dx/x ~ (G²Mμ)/(c⁴ar)　

Вычисляя время до столкновения звезд, учтем, что суммарная энергия системы (кинетическая плюс потенциальная) составит

E = — GMμ/a + m₁ω²a₁²/2 + т₂ω²а₂²/2

E = — GMμ/a + m₁ω² а²/2

E = — GMμ/a + — GMμ/2a

E = — GMμ/2a

Дифференциальное уравнение для ее изменения во времени получается из условия равенства этой энергии и энергии гравитационных волн [129]

dE/dt = GMμ/2a² x da/dt

dE/dt = — L

GMμ/2a² x da/dt = — (32G⁴M³μ²)/5c⁵a⁵

da/dt = — (64G³M²μ/5c⁵a³)

dt/da = — (5c⁵a³/64G³M²μ)

Интегрирование элементарно и привносит дополнительный множитель 1/4:

t = — (5c⁵a⁴/256G³M²μ)　

Здесь предполагается, что звезды столкнутся при t=0.

В этих выкладках я следовал гл. 35–36 учебника С. W Misner, К. S. Thorne and J. A. Wheeler, Gravitation, W. Н. Freemann, New York, 1970 [Имеется русский перевод: Ч. Мизнер, К. Торн, Дж. Уилер, Гравитация. В 3-х тт. M.: Мир, 1977.] (далее MTW). Уравнение для энергии излучения L с точностью до коэффициентов пересчета из системы единиц, где G = с = 1, совпадает с уравнением MTW (36.16а), а уравнение для времени столкновения t ― с уравнением MTW (36.17Ь). Промежуточные вычисления основаны на уравнении MTW (36.1).

На моем сайте можно загрузить интерактивный Java-апплет, иллюстрирующий пространственно-временную диаграмму гипотетической системы двух закороченных червоточин. Для работы с ним ваш браузер должен поддерживать Java. Апплет занимает 71 Кбайт, так что, если у вас медленный Интернет, загрузка отнимет какое-то время. Две красные вертикальные прямые соответствуют мировым линиям горловин одной червоточины, а две синие — мировым линиям горловин другой червоточины. Все, что проходит в горловину одной червоточины, немедленно возникает из горловины другой. Термин «немедленно» следует трактовать в контексте системы отсчета, связанной с первой червоточиной. Изменяя наклон синих прямых, вы можете варьировать относительную скорость прохождения фотонов по червоточинам и наблюдать, как влияет это изменение на путь пробного фотона, отмеченный фиолетовыми линиями.

Вид окна работающей программы

В теории Кожух каждая элементарная частица представляет собой горловину червоточины. В двумерном пространстве, показанном на следующем рисунке, в центре каждой червоточины присутствует сингулярность.

Кажущаяся сингулярность в центре червоточины

Однако, если вложить червоточину в пространство с числом измерений, большим на 2, сингулярность устраняется. Теперь каждая точка может занимать любую позицию на поверхности сферы. Эта сфера называется стандартным расслоением теории Кожух.

Стандартное расслоение теории червоточин Уилера-Кожух

Теперь в измерениях высшего порядка пути через червоточину уже не сходятся в точке сингулярности.

В трехмерном пространстве гравитационный потенциал обратно пропорционален квадрату расстояния.

В пятимерном же пространстве он обратно пропорционален четвертой степени расстояния. Дно колодца лежит ниже, но уплощение потенциальной поверхности на выходе из него происходит быстрее.

Центробежная сила от числа измерений не зависит. Для данного значения орбитального углового момента отталкивание обратно пропорционально кубу расстояния.

Комбинированный потенциал, учитывающий как гравитационное взаимодействие, так и центробежную силу, в трех измерениях проявляет «энергетический желоб», разрешающий устойчивые круговые или эллиптические орбиты.

В пяти измерениях присутствует «энергетический водораздел», и разрешены только неустойчивые круговые орбиты. Даже на них движение требует постоянного притока энергии. Ни один естественный астрономический объект там долго не продержится.

В пяти измерениях электростатическое притяжение между положительно заряженным ядром и отрицательно заряженным лептоном (аналогом электрона) математически эквивалентно гравитационному взаимодействию. Стабильных волновых функций нет. Лептонная волна сжимается до размеров ядра. А внутри последнего колодец потенциальной энергии принимает форму умеренно уплощенного параболоида:

Если скомбинировать его с потенциалом орбитального углового момента лептона, появляется еще и центральный пик:

На нижнем энергетическом уровне, однако, орбитальный угловой момент у лептона отсутствует. Волновая функция обладает идеальной сферической симметрией, вероятностное распределение для лептона по поверхности потенциальной энергии колоколообразно для любой плоскости, проходящей через центр ядра:

На следующем уровне имеется угловой момент, и волновая функция «дрейфует» от центра ядра:

Если скомбинировать последнюю функцию со своим аналогом, повернутым на 90 градусов в любом направлении и дополнительно умноженным на i (V‾— 1), получим собственные функции углового момента (то есть волновые функции, для которых значение этого параметра определено) с шагом ± 1 ед. Они показаны ниже, с цветовой кодировкой комплексной фазы.

Поверхность гиперсферы в пятимерном пространстве описывается уравнением

где х, у z, и, W ― пространственные координаты, а система координат отцентрирована по центру гиперсферы. Предположим, что гиперсфера вращается как целое. Общее выражение для скорости любой точки вращающегося тела не зависит от числа измерений и дается уравнением

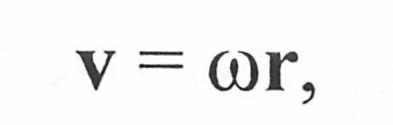
где матрица угловых скоростей тела обозначена как Ω, а вектор точки - как r. Матрица должна обладать свойством антисимметричности, то есть Ω_ij = ―Ωji. $ Чтобы доказать это, заметим, что Ω ― матрица производных по времени от компонент линейного преобразования позиции точки в момент времени t=0 в позицию, соответствующую повороту. Матрица преобразования M(t) диктует такой поворот пары базисных векторов идеально жесткого тела е_i и е_j, что их произведение, измеряющее угол между векторами, остается неизменным. Скорость изменения этого произведения во времени, следовательно, равна нулю.

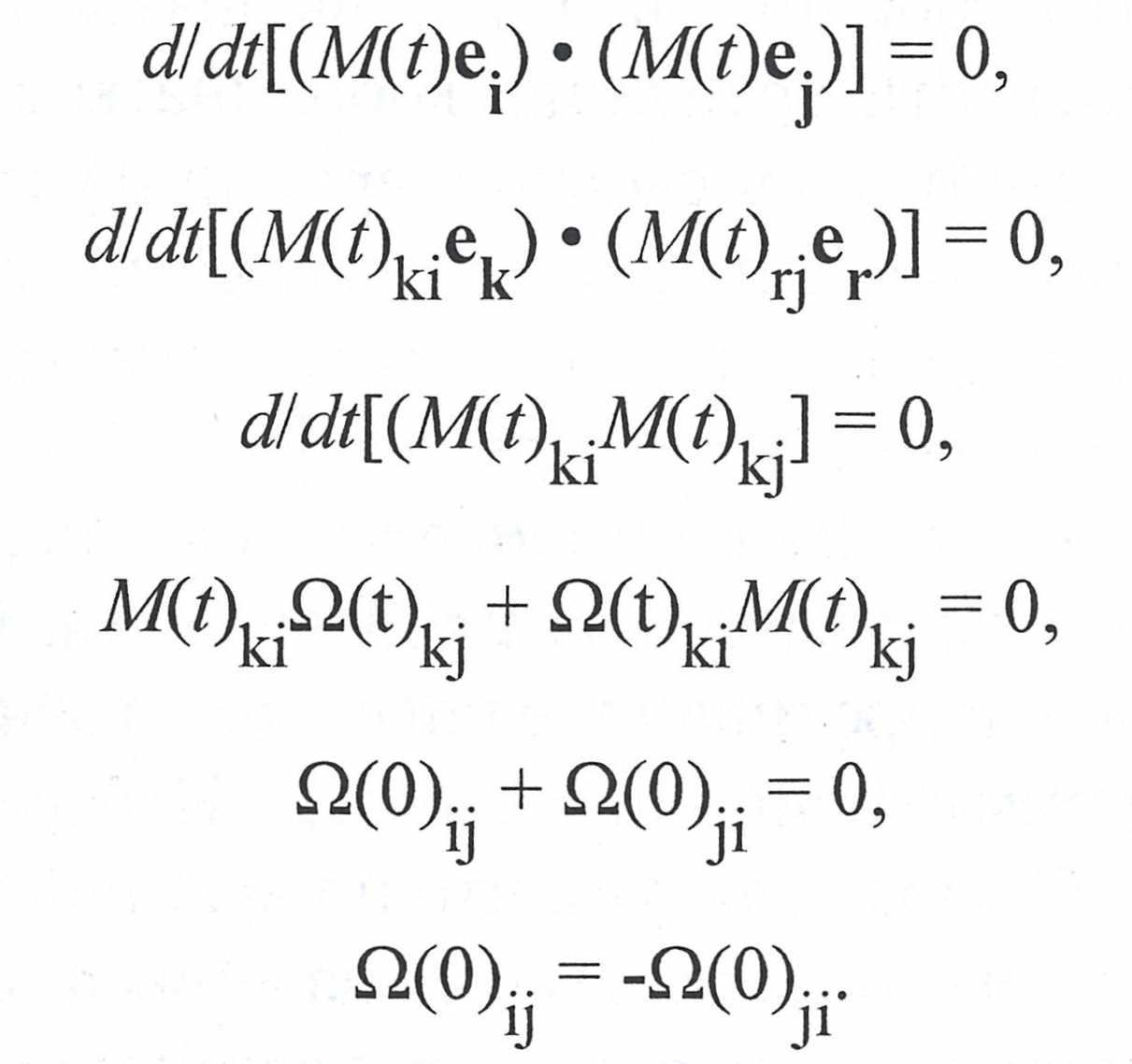
Здесь мы использовали соглашение о суммировании, введенное Эйнштейном, и просуммировали по всем значениям повторяющихся индексов (например, k и r). Чтобы получить четвертое уравнение из третьего, заметьте, что M(O) ― просто матрица идентичности. Переходя к искомому соотношению, мы отбросили временную зависимость элементов матрицы угловых скоростей, поскольку предполагаем, что на тело не действуют никакие внешние силы, а значит, Ω постоянна. В пяти измерениях общая антисимметричная 5 х 5-матрица Ω будет иметь 10 независимых параметров, но всегда можно выбрать базис, в котором она приводится к каноническому виду:

Отметим, что координаты х и у выбраны так, что они лежат в одной плоскости вращения, координаты z и и - в другой, а координата w лежит в плоскости, перпендикулярной им обеим. Чтобы понять, почему всегда можно выбрать такой базис, сперва учтем, что определитель любой антисимметричной матрицы N x N, где N ― нечетное число, равен нулю. Это так, потому что detΩ = detΩ^T, где T означает транспонирование, а определитель - собственно, N ― членная сумма произведений, в которой знаки везде изменены на противоположные для транспонированных компонент антисимметричной матрицы. Итак, detΩ^T = ―(detΩ) для нечетных N. Отсюда следует, что по крайней мере один ненулевой вектор в нуль-пространстве Ω наверняка существует. Выбирая его как опорное направление координаты w, ось вращения, мы «заполняем» последние столбец и строку матрицы Ω нулями. Задача сводится к четырехмерной. Четырехмерный случай будет рассмотрен дальше.

Пока же перемножим вектор для общей точки r = (x,y,u,z,w) на каноническую матрицу и получим

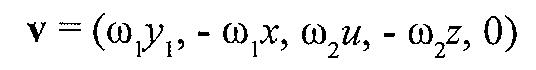
Итак, для любой точки c x=y=z=u=0 скорость равна нулю. Набор таких точек составляет ось вращения тела - ось w. Сечение осью исходной гиперсферы даст два полюса, на которых w = ±R. Физически возможен, но космологически маловероятен случай, когда ω₂ = 0, то есть, чтобы скорость стала равной 0, достаточно удовлетворить условию х = у = 0. При этом остальные три координаты можно выбирать произвольно: они образуют трехмерный объем. Сечение объектом гиперсферы даст единственный полюс: двумерную сферу

z² + u² + w² = R².

Два экваториальных круга:

В первом случае скорость вращения поверхности равна ω₁R, а во втором ― ω₂R. Итак, в пятимерном пространстве объекты могут вращаться одновременно с различными скоростями.

Перейдем к рассмотрению четырехмерного случая. Здесь общая матрица угловых скоростей задается шестью параметрами:

Отметим, что всегда можно ориентировать систему координат так, чтобы матрица А приводилась к каноническому виду. Один из способов это сделать требует отыскания собственных векторов AA, матричного произведения А на себя саму. Это действительная симметричная матрица, и, следовательно, у нее четыре ортогональных собственных вектора. Они образуют пары с собственными значениями ― ω₁² и ― ω₂². Смысл этого явления легко выяснить из геометрических аналогий: действуя А на любой вектор, лежащий в одной из плоскостей вращения, мы поворачиваем этот вектор на 90 градусов и умножаем на соответствующую компоненту ω. Действуя А дважды, мы восстанавливаем исходное значение вектора и умножаем его компоненты на ω². Каждая пара собственных векторов лежит в одной из плоскостей вращения.

Другой способ заключается в применении линейного оператора - звезды Ходжа. Обычно дуальная матрице M матрица Ходжа записывается как ★ М, отсюда кодовое обозначение макросферы в Диаспоре. В контексте четырехмерной евклидовой геометрии звезда Ходжа отображает плоскости на другие плоскости. Например, если четыре используемых нами координаты обозначить как x,y,z,u, то дуальная плоскость Ходжа для плоскости ху ― плоскость zu. Аналогичным образом находятся и другие дуальные плоскости. Ситуация несколько осложняется тем, что при повороте в каждой плоскости придется выбирать из двух направлений вращения. Но, рассматривая А как сумму поворотов в шести координатных плоскостях, мы получаем дуальные плоскости для каждой из них без особого труда. Придется лишь поменять несколько знаков, чтобы соблюсти выбранную ориентацию, и вместо коэффициентов, соответствующих, например, координатам х и у, написать коэффициенты, соответствующие, например, координатам z и и. Можете самостоятельно проверить, что получается

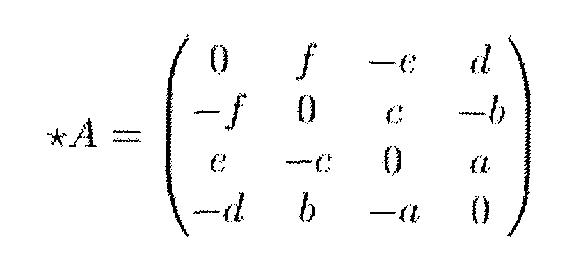
Теперь мы хотели бы расписать А как сумму по вращениям в двух плоскостях: в одной плоскости, матрицу которой мы обозначим как S, и перпендикулярной к первой, чью матрицу мы обозначим как ★S. Иными словами, следует выбрать S, ω₁, ω₂ так, чтобы

Действуя оператором Ходжа, а также учитывая, что двукратное его применение восстанавливает исходную матрицу, получим

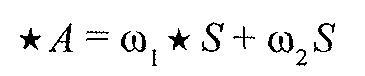
Первое из этих уравнений домножим на ω₁ , а второе ― на ω₂. Вычтем их друг из друга. Имеем

Чтобы найти значения ω₁, и ω₂, заметим, что результат применения матрицы S к вектору, перпендикулярному ее плоскости, равен нулю. Это возможно только в том случае, если определитель матрицы detS=0. Выпишем матрицу в явном виде и вычислим ее определитель. Это действие довольно утомительно.

Здесь мы ввели обозначения

Потребуем нормализовать матрицу S, чтобы |S|² = |★S|² = 1. Тогда значения ω₁ и ω₂ можно найти по отдельности. Между «амплитудами» исследуемых матриц имеется пифагорово соотношение. Как только А разбита на дуальные пары, становится легко найти индивидуальные скорости вращения. 　

Если мы хотим выбрать новые координаты так, чтобы А привести к каноническому виду, следует также определить пару ортогональных векторов для плоскости, определяемой S, и пару ― для плоскости, определяемой ее ходжевской дуaлью ★S. Это стандартная техника линейной алгебры для работы с такими матрицами.