Глава 1 Все, что вы хотели узнать о числе π, но боялись спросить
Совместны у круга начало и конец.
Гераклит
Число π — самое известное, самое изученное, самое знаменитое и самое упоминаемое. Важность числа π невозможно преувеличить. Его десятичная запись начинается так:
3,14159265358979323846264338327950288419716939937510…
и этих пятидесяти магических цифр достаточно для любых практических вычислений. В математике или физике редко встретится задача, для которой необходимо использовать более десяти знаков π. Для простейших вычислений используются приближенные значения: 3,14 или 3,1416.
Айзек Азимов как-то написал: «Если бы Вселенная имела форму сферы диаметром 80 миллиардов световых лет, то с помощью 35 знаков числа π мы смогли бы вычислить длину ее небесного экватора с погрешностью меньше одной миллионной доли сантиметра».
Если мы запишем число π, рассчитанное на компьютере на данный момент, цифрами размером с эту книгу, то получившийся ряд цифр опишет 500 витков вокруг экватора Земли. Точно известно, что последовательность 0123456789 встречается в числе π начиная с 17387594880-го знака. Какой же наивной кажется убежденность известного голландского математика Лёйтзена Эгберта Яна Брауэра (1881–1966), который считал, что искать эту последовательность в числе π бессмысленно, поскольку необходимое для этого число знаков никогда не будет вычислено.
В XXI веке мы наконец нашли неоспоримую пользу от вычисления числа π с такой точностью: для тестирования суперкомпьютеров используются сложные вычисления, результат которых должен быть заранее известен, и для этого идеально подходит расчет знаков числа Я.
Число π не появилось из пустоты, как это можно было бы предположить. Оно возникло как результат несложных наблюдений. Соотношение между длиной окружности L и ее диаметром d постоянно:
L/d = π.
Или, что то же самое,
L = π∙d = π2r = 2πr,
где r — радиус окружности, d = 2r.
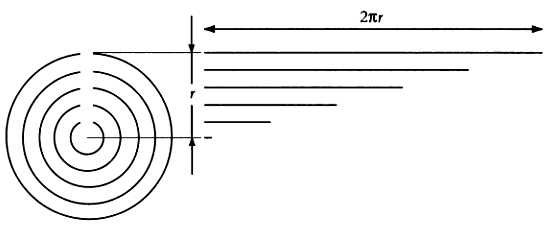
Отношение длины окружности к ее диаметру постоянно. Это соотношение интуитивно понятно и становится очевидно после несложных наблюдений. С увеличением диаметра (диаметр равен удвоенному радиусу r) пропорционально возрастает длина окружности.
Чем больше диаметр колеса, тем больше (и пропорционально больше) расстояние, пройденное точкой колеса при полном обороте. Иными словами,
длина окружности/диаметр окружности = константа ~ 3,14.
Знак ~ читается как «приближенно равно». На протяжении большей части истории числа π ученые старались сделать это приближение как можно более точным, находя всё новые знаки справа от 3,14.
Математики использовали все свое умение, чтобы рассчитать число π с наиболее возможной точностью, добавляя десятичные с героическими усилиями.
ВЫПРЯМЛЕНИЕ ОКРУЖНОСТИ
Выпрямление кривой означает измерение ее длины. В простейшей задаче о выпрямлении кривой речь идет об окружности.
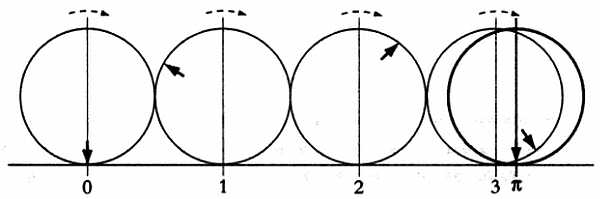
При качении окружности длины р по прямой без скольжения окружность описывает один оборот, проходя расстояние, равное диаметру d, π раз. Этот процесс называется выпрямлением окружности. По результатам выпрямления окружности получим p/d = π.
* * *
Долгое время считалось, что когда-нибудь будет найдена последняя цифра числа π, но в 1882 году немецкий математик Фердинанд фон Линдеман (1852–1939) доказал, что это невозможно. Не существует и никогда не будет найдено способа получить «точное» значение π, пользуясь только циркулем и линейкой. Далее в этой книге мы попытаемся объяснить, почему это так.
Сначала число π имело другое название. Хотя к этому символу обращались многие математики, в частности Уильям Отред (1574–1660), Исаак Барроу (1630–1677) и Дэвид Грегори (1659–1708), «официально» его утвердил Уильям Джонс (1675–1749) в 1706 году в работе Synopsis Palmariorum Matheseos, где он использовал букву π, первую букву греческого слова «περιφε'ρεια» — «окружность». Впоследствии великий Леонард Эйлер (1707–1783), который сначала оперировал символами «с» и «р», остановился на греческой букве π, после чего это обозначение начало медленно, но верно распространяться в научном мире. Однако в XX веке в Египте число «пи» маркировали арабской буквой ta по нескольким причинам, в том числе из-за нежелания пользоваться европейскими обозначениями.
Сегодня символ π используется в математике в основном для обозначения числа π, но он также выполняет и другие задачи. Так, π(x) обычно отмечают функцию, показывающую «количество простых чисел, не превосходящих х». Если говорить о менее серьезных вещах, то этой буквой также обозначают гептамино — фигуру, состоящую из семи квадратов, соединенных сторонами, как показано на рисунке:

Многие авторитетные ученые, в том числе и Эйнштейн, считали число π фундаментальным в описании Вселенной. В том или ином виде число π всегда будет всплывать в описании любого явления природы, связанного с окружностями, кругами или вращением, подобно тому как пробка всплывает на поверхность воды. Как и другие константы, π всегда будет сопровождать нас.
С другой стороны, множество людей, которым в той или иной степени интересна нумерология, ищут число π буквально повсюду, как если бы существовала некая теория заговора, связанная с π. Так называемая постоянная тонкой структуры, обозначаемая как ОС, — излюбленная жертва поклонников числа π. Нобелевский лауреат Вернер Гейзенберг (1901–1976) много лет назад предположил, что
1/α = 24∙33/π
Но Гейзенберг был не единственным, кто искал связь между этими константами. В различных трудах фигурируют и другие подобные соотношения достаточно высокой точности, например:

ПЛАНЕТА МАЛЕНЬКОГО ПРИНЦА
Существует любопытный факт, который далеко не очевиден. Так как для окружности выполняется соотношение
длина/диаметр — константа,
то при увеличении знаменателя в некоторое число раз числитель увеличится в это же число раз. Проиллюстрируем это простым примером. В сказке французского писателя и авиатора Антуана де Сент-Экзюпери (1900–1944) «Маленький принц» главный герой обходит свою планету и чистит вулканы. Допустим, что он обходит всю планету по меридиану. Рост принца ровно 1 метр. Если он пройдет 1000 метров, какое расстояние пройдет его голова? Будем производить все расчеты в метрах. Так как Маленький принц проходит 1000 метров и
длина окружности = 2π∙r,
очевидно, что
пройденное расстояние = 1000 = 2π∙r.
Рост принца равен 1 метру. Приняв за С расстояние, пройденное его головой, получим
C = 2π∙(r + 1).
Вычтем первое равенство из второго. Имеем:
расстояние в метрах, пройденное головой — расстояние в метрах, пройденное ногами
С = 1000 — 2π∙(r + 1) — 2πr = 2π∙(r + 1 — r) = 2π ~ 6,28.
Разница составляет 6,28 м. Любопытно, что радиус планеты никак не влияет на это значение.
Фактически, если мы прибавим к радиусу исходной окружности 1 метр, ее длина увеличится на 6,28 м. Если бы радиус астероида составлял 1000 километров, то дополнительное расстояние, пройденное головой Маленького принца, осталось бы таким же: 6,28 м.

Обложка «Маленького принца» Антуана де Сент-Экзюпери.
Число π — не только соотношение между длиной окружности и ее диаметром. Удвоенное отношение между площадью круга и площадью вписанного в него квадрата также равно π. Как нам известно из школы, площадь круга радиуса г равняется
S = πr2.

Так как площадь квадрата равна квадрату его стороны, по теореме Пифагора получим
S/Площадь вписанного квадрата = πг2/2r2 = π/2
Но откуда мы знаем, что число π, используемое для расчета площади, — это то же самое π, с помощью которого рассчитывается длина окружности? Несомненно, это одно и то же число, однако доказать это не так просто. Строгое доказательство появилось только благодаря усилиям Архимеда.
Умы древних математиков волновала задача о построении квадрата, по площади равного данному кругу. Задача имела чисто практическое применение: площадь квадрата вычисляется элементарно, тогда как расчет площади круга был сложен и результатом являлось лишь приближенное значение. Во времена расцвета Древней Греции к этой задаче добавилось еще одно ограничение: искомый квадрат нужно было построить только с помощью циркуля и линейки. Этот метод считался «чистым», «божественным» и соответствовал духу греческой философии. В этом и заключается задача о квадратуре круга: необходимо построить искомый квадрат, используя только циркуль и линейку конечное число раз. Математики бились над задачей, решение которой всякий раз казалось столь близким и неизменно ускользало от них.
На протяжении веков все геометры пытались решить задачу о квадратуре круга, что равносильно построению отрезка длиной π с помощью циркуля и линейки, и всякий раз им удавалось найти лишь более точное приближенное значение и добавить еще один знак к десятичной записи π. Алгебраически задача о квадратуре круга площадью πr2 равносильна нахождению квадрата со стороной l такого, что
πr2 = l2.
Иными словами, необходимо найти такое l, что
l = √(πr2) = r√π,
что тождественно нахождению √π с помощью циркуля и линейки. Если значение √π найдено, то найти π с помощью циркуля и линейки элементарно, построив прямоугольный треугольник с катетами 1 и √π, а затем продлив перпендикуляр к гипотенузе полученного треугольника до пересечения с продолжением единичного отрезка.
В силу подобия треугольников ABD и ADC выполняется соотношение АВ/AD = AD/АС, откуда AD2 = АВ∙АС.

Подставляя известное значение АВ = 1 и найденное AD = √(1 + π), получаем: 1 + π = АС, то есть ВС = π.
Если бы значение π было определено, было бы возможным найти √π и решить задачу о квадратуре круга. Но за этой простой формулировкой кроется длинная история, герои которой безуспешно пытались достичь заветной цели, всякий раз все ближе подходя к ней. Очередной талантливый геометр находил следующий знак π и тем самым неявно продвигал всю математику в целом на шаг вперед.
РАДИАН И π
В математике для измерения углов не используются градусы, минуты и секунды. Также не применяются грады и метрические минуты и секунды. Появление математического анализа (производных, интегралов и пр.) привело к тому, что начала использоваться более естественная единица измерения, пусть на первый взгляд она и кажется сложнее. Радиан определяется как угловая величина дуги, длина которой равна ее радиусу.

Так как длина всей окружности равна 2πr, то всю окружность можно представить в виде дуги в 2π радиан. Таким образом,
1 радиан — 360/2π градусов ~ 57°17′5''
Часто применяются следующие соотношения:
30° = π/6; 60° = π/3; 90° = π/2; 180° = π; 360° = 2π.
История числа π: гомеровская Греция
Из нескольких стихов Библии следует, что π = 3. В Библии это значение упоминается в описании постройки круглого алтаря, поэтому не следует расценивать это как попытку рассчитать его точное значение. Приведем цитату из 3-й книги Царств (7:23) для любопытного читателя: «И сделал литое [из меди] море — от края его до края его десять локтей — совсем круглое, вышиною в пять локтей, и снурок в тридцать локтей обнимал его кругом».
Проницательный читатель заметит, что значение числа π в этом тексте принято равным 3.
В египетском папирусе Ахмеса (древнеегипетское учебное руководство по математике, датированное примерно 1650 г. до н. э.) также неявно упоминается π. В задаче под номером 50 из 87 говорится: «Круглое поле имеет в диаметре 9 хет (1 хет ~ 50 м). Какова площадь поля?» На современном языке площадь этого круга выражается так:
π∙(9/2)2 = π∙(81/4)
В самом папирусе Ахмеса предложено такое решение:
(64/81)∙d2
где d — диаметр. Так как d = 9, получим
π∙(81/4) = (64/81)∙d2 = (64/81)∙92 = (64/81)∙81;
π = 256/81 ~ 3,160493827.

Согласно папирусу Ахмеса, квадрат со стороной 8 равен по площади кругу диаметра 9.
Однако это значение менее точно, чем полученное египтянами в Гизе еще в 2600 г. до н. э. Соотношение периметра и высоты пирамид Гизы равно 22/7, хотя считается, что оно подчинялось неким божественным законам, которым следовали архитекторы того времени. Многие исследователи считают это соотношение приближенным значением ТС, которое загадочным образом определили строители пирамид. Если мы допустим, что соотношение периметра и высоты пирамид не случайно, получим
π = 22/7 = 3,142…,
что соответствует π с хорошей точностью.
В Вавилонии в этом смысле прогресс шел медленнее: на глиняной табличке из древнего города Суса, датированной примерно 200 г. до н. э., приведено значение π, равное 25/8 = 3,125.
В ведических текстах Древней Индии, относящихся к IX веку до н. э., приводятся различные значения π, рассчитанные для разных практических задач. Наиболее точное значение основано на астрономических вычислениях и содержится в «Шата-патха-брахманы»: π = 339/108 = 3,1388…
История числа π: Архимед
Перенесемся в Древнюю Грецию — родину одного из величайших умов человечества, Архимеда из Сиракуз. Возможно, еще в V веке до н. э. вычислением числа π занимался Анаксагор, но письменных свидетельств этого не сохранилось. Мы не будем приводить здесь выкладки Архимеда о расчете приближенного значения π, так как они сложны и объемны. Оставим их историкам науки. Попробуем объяснить метод Архимеда простым и доступным образом, используя современное понятие предела. Представим себе многоугольник, вписанный в окружность, подобный тому, что изображен на рисунке.
Заметим, что он состоит из треугольников с основаниями Ь и высотой h. Общая площадь n треугольников, примерно равная площади круга, равна
Sn = п площадь треугольника.
Таким образом,

Перейдя к пределу и увеличивая число треугольников так, что n —> 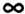 , получим
, получим

так как

и придем к следующему заключению:

Архимеду было неизвестно современное определение предела, и он использовал так называемый метод исчерпывания, созданный Евдоксом Книдским (400–347 до н. э.). Для этого Архимед использовал вписанные и описанные многоугольники, как показано на рисунке. Окружность заключалась между вписанным и описанным многоугольниками, соответственно, была ограничена и площадь окружности. С ростом числа углов многоугольников оценка площади окружности становилась все точнее.

Схема, на которой изображен так называемый переход к пределу, поможет понять, почему площадь круга равняется πr2:
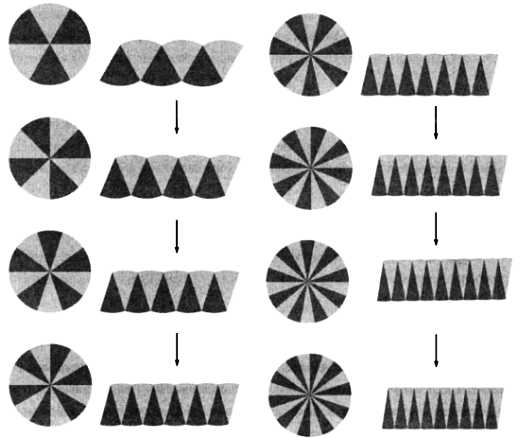
Мы видим, как формируется криволинейный параллелограмм и его стороны постепенно распрямляются. Вспомним, что площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне. Высота постепенно приближается к значению радиуса r, а основание — к половине длины окружности. Площадь параллелограмма стремится к
r∙(l/2) = r∙(2πr/2) = rπr = πr2
Архимед вычислил верхнюю и нижнюю оценку значения π:
223/π = 3,140845… < π < 22/7 = 3,142857…
с отменной точностью.
АРХИМЕД ИЗ СИРАКУЗ (ОК. 287 — ОК. 212 ГГ. ДО Н.Э.)
Греческий инженер, физик, астроном и математик Архимед считается важнейшим ученым античности и одним из величайших умов человечества. В области математики фигурами сопоставимой величины можно назвать лишь Ньютона, Гаусса и фон Неймана. Его вклад в науку неоценим. Он создал червячную передачу, параболические зеркала, многочисленные системы блоков (полиспасты) и многие другие механизмы. Наверное, самым значимым стал открытый им закон гидростатики, известный нам как закон Архимеда. Образ Архимеда, который выскакивает из ванной и кричит «Эврика!» («Нашел!»), стал классическим образом первооткрывателя. Его открытия в математике бессчетны: помимо вычисления числа к он определил периметр, площадь, объем и центр тяжести для множества геометрических фигур и тел (в частности, для сферы, цилиндра, параболы, спирали и пр.), изучал диофантовы уравнения, построил счисление, позволяющее записывать и называть весьма большие числа, и так далее.
Он умер во время осады Сиракуз, при обороне которых использовались придуманные им механизмы. Согласно Плутарху, Архимед рассматривал чертеж на песке, когда к нему подошел римский солдат. Архимед настойчиво просил его подождать, сказав: «Не трогай мои чертежи», после чего разгневанный солдат зарубил Архимеда мечом. Плутарх пишет, что смерть Архимеда возмутила римского генерала, который считал ученого очень ценной добычей.
На могиле великого геометра изображен шар, вписанный в цилиндр. Соотношение между объемами цилиндра и вписанного шара открыл именно Архимед.

Одно из многочисленных изобретений, приписываемых Архимеду, — система бронзовых зеркал. С помощью этих зеркал защитники Сиракуз поджигали римские корабли, фокусируя на них солнечные лучи.
* * *
Метод, использованный Архимедом, стал фактически обязательным к применению в последующие несколько веков. Он доступен, прост и понятен. Математический гений Архимеда создал настоящее чудо. По существу, Архимед придумал алгоритм расчета π с любой точностью. Чтобы использовать этот алгоритм, нужен только калькулятор или компьютер и одна рекуррентная формула. Если n — число сторон вписанного или описанного многоугольника, а аn и Ьn — периметры таких многоугольников, то
a2n = 2anbn/(an + bn),
b2n = √(a2nbn).
В этом и заключается суть алгоритма Архимеда — рекуррентной формулы, с помощью которой рассчитывается приближенное значение π, точность которого повышается по мере роста п. Всегда выполняется соотношение аn > π > Ьn.
Используя алгоритм Архимеда начиная с правильного шестиугольника, в котором а0 =4√3 и b0 = 6, получим:
3,00000 < π < 3,46410
3,10583 < π < 3,21539
3,13263 < π < 3,15966
3,13935 < π < 3,14609
3,14103 < π < 3,14271.
Рассчитав значения этого неравенства для правильного 96-угольника, мы получим оценку числа π, вычисленную самим Архимедом.
Примерно в 20 году до н. э. известный римский архитектор, военный инженер и писатель Марк Витрувий Поллион (ок. 85 — ок. 20 гг. до н. э.), более известный как Витрувий, создал монументальный труд «Десять книг об архитектуре», где используется соотношение, найденное в Месопотамии: π = 25/8. Сам Витрувий произвел оценку числа π с помощью колеса с нанесенными отметками. Тем не менее он известен потомкам не поэтому, а благодаря рисунку Леонардо да Винчи «Витрувианский человек» с каноническими пропорциями человека.
«Витрувианский человек» с каноническими пропорциями тела человека, определенными древнеримским архитектором Витрувием. Знаменитый рисунок Леонардо да Винчи (1452–1519).
Несмотря на столь широкую известность, Витрувий не добился более точного результата, чем Архимед. Это удалось египетскому астроному, астрологу и географу греческого происхождения Клавдию Птолемею (ок. 100 — ок. 170 гг.). Для расчетов он использовал 120-угольник, получив поразительно точный результат π = 3 + (17/120) = 3,141666… К сожалению, это не принесло ему заслуженной славы среди потомков. Он известен благодаря одному из своих трудов, «Альмагесту» в 13 книгах, название которого с древнегреческого переводится как «Великое построение». С этой книги началась традиция создания трудов, описывающих все известные на данный момент знания. Фактически «Альмагест» Птолемея не терял актуальности вплоть до появления работ Коперника.
Уделяя основное внимание западной культуре, мы часто забываем, что в эпоху Античности процветали и другие города помимо вавилонских, греческих, римских и египетских. Западная цивилизация наблюдала появление числа π, но что же происходило в это время на далеком Востоке?
Например, в Китае этому вопросу уделяли внимание Чань Цан (ок. 220 г. до н. э.), который принял значение π равным 3, и другие математики. Чжан Хэн (78-139 гг.н. э.), который занимался астрономией и математикой и изобрел прибор для регистрации землетрясений, в одной из своих книг рассчитал значение π = 736/232 = 3,1724… При вычислении объема шара, вписанного в куб, он использовал приближенное значение π = √10 = 3,162277…
Ван Фань (217–257 гг. н. э.) в 250 году рассчитал приближенное значение π = 142/45 = 3,155555…
Математик Лю Хуэй (ок. 220 — ок. 280 гг.) является автором комментариев к «Математике в девяти книгах». Именно по этим комментариям, изданным в 263 году, нам известно о существовании этого ученого и о его достижениях. Лю Хуэй приводит рекуррентную формулу для расчета периметра правильного многоугольника, имеющего 3∙2k сторон при известном периметре многоугольника, число сторон которого равно 3∙2k-1. Лю Хуэй рекомендовал использовать значение π = 3,14, хотя сам он вычислил значение π = 3,141592104…, для чего потребовалось использовать многоугольник с 3072 сторонами.
Несколько веков спустя Цзу Чунчжи (429–500 гг.), ученый и математик, который разработал новый календарь, с превосходной точностью оценил верхнюю и нижнюю границы числа π:
3,1415926 < π < 3,1415927.
Он также рекомендовал использовать значение 22/7 для простых вычислений и 355/113 — для более сложных.
Перенесемся в Древнюю Индию, где выдающийся мудрец Ариабхата (ок. 476–550 гг.) получил значение π, равное 3,1416, используя многоугольник с 384 сторонами.
Брахмагупта (598–665 гг.), вне всякого сомнения наиболее одаренный индийский математик, создал объемный труд «Брахма-спхута-сиддханта», где, к сожалению, приводится достаточно неточная оценка
π = √10 = 3,162277…
Марка, выпущенная в 1999 году Федеративными Штатами Микронезии, на которой изображен метод Лю Хуэя для расчета приближенного значения π.
Более точное значение было получено лишь в XII веке усилиями Бхаскары II (1114–1185) в его книге «Лилавати». Книга носит имя его дочери, которая, если судить по важности этого труда, должна была быть прекраснейшей девушкой — удивительно, но именно это и означает имя Лилавати. Бхаскара II приводит π = 3917/1250 = 3,1416.
Наша система счисления является позиционной с основанием 10. В ней используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, имеющие индо-арабское происхождение. Мы не уделяем этому особого внимания, но именно появление этой системы счисления способствовало развитию торговли: западная цивилизация получила математический инструмент, благодаря которому вычисления стали доступны для всех.
Индо-арабские цифры в том виде, в каком они впервые появились в западном мире (974–976 гг.) в Альбельденском (Вигиланском) кодексе, названном так по имени монаха — автора иллюстраций для этого собрания документов.
Подробная история индо-арабских цифр выходит за рамки нашего повествования. Отметим лишь, что свое название они получили по месту происхождения. Удивительно, но на Западе эти цифры и система счисления в целом появились лишь в X веке в «Книге Абака» Леонардо Пизанского (ок. 1170–1250), также известного как Фибоначчи. Индо-арабские цифры распространились в Европе с быстротой молнии, особенно среди торговцев и образованных людей. Расчеты в новой системе счисления перестали быть такими проблематичными благодаря простым правилам умножения и деления. Цивилизация сделала медленный, но важный шаг вперед.
На середине нашего повествования мы впервые встречаем имя Фибоначчи, который в 1220 году вычислил приближенное значение π = 3,141818 в одной из своих работ «Практика геометрии» (Practica geometriae), несколько вольно применив метод Архимеда.
Но не будем забегать вперед. Обратим внимание на фигуру Мухаммеда ибн Муса аль-Хорезми (ок. 780–850 гг.), также называемого аль-Хорезми. От видоизмененного имени аль-Хорезми берет начало термин «алгоритм». Аль-Хорезми является автором «Книги о восполнении и противопоставлении», от арабского названия которой происходит слово «алгебра». Его труды, переведенные на Западе, имели огромнейшее влияние. Аль-Хорезми также рекомендовал использовать значение 3,14 в простых расчетах и 3,1416 — в сложных, например, в астрономии.
Героический образ аль-Хорезми, запечатленный на советской марке 1983 года (аль-Хорезми жил на территории современного Узбекистана).
В 1424 году другой персидский ученый Джамшид ал-Каши (1380–1429) из Самарканда рассчитал значение 2π с точностью до 9 знаков, используя шестидесятиричную систему счисления (в ней числа записываются следующим образом: 1/60 = 0,1; 1/602 = 1/360 = 0,01 и т. д.). После перевода в десятичную систему счисления это соответствует точности в 16 знаков после запятой. Ал-Каши вычислил:
2π = 6 + 16/60 + 59/602 + 28/603 + 1/604 + 34/605 + 51/606 + 46/607 + 14/608 + 50/609 + …,
используя многоугольники с числом сторон 3∙228. За четверть века до него, в 1400 году, индийский математик Мадхава из Сангамаграма (ок. 1350 — ок. 1425) вычислил π с точностью до 13 знаков. Кроме того, расчеты Мадхавы отличаются оригинальностью: в них впервые используется бесконечный ряд для оценки значения π. Формула Мадхавы позднее стала известна в западном мире как «ряд Лейбница», но Мадхава открыл ее намного раньше:
π/4 = 1–1/3 + 1/5 — 1/7 + 1/9 — …
Этот ряд сходится очень медленно. Чтобы получить более или менее приемлемый результат, необходимо сложить тысячи членов ряда. Мадхава использовал этот ряд в преобразованном виде:
π = √12∙[1 — (1/3∙3) + (1/5∙32) — (1/7∙33) +…]
что и помогло ему вычислить π.
Немецкий ученый Валентин Отто (ок. 1550–1603), ярый последователь Коперника, в 1573 году рекомендовал использовать π = 355/113 ~ 3,1415929… Однако это не идет ни в какое сравнение с результатами, полученными спустя некоторое время с помощью передовых способов вычисления, а не просто путем аккуратно проведенных расчетов. Французский математик Франсуа Виет вычислил девятый знак числа π обычным способом, используя метод Архимеда и многоугольник с 393216 (6∙216) сторонами. Хотя ему и удалось вывести важную формулу, связанную с π, он не смог применить ее из-за сложных вычислений: его формула включает вычисление квадратного корня из квадратного корня числа. На современном языке математики формула Виета записывается следующим образом:
Вывод этой и других формул подробно объясняется в главе 4.
ФРАНСУА ВИЕТ (1540–1603)
Строго говоря, Виета нельзя назвать профессиональным математиком: он был адвокатом, а после восшествия на престол Генриха IV занял должность при дворе и даже служил королевским советником. Легендарную известность ему принесла криптография: он с легкостью расшифровывал послания испанского монарха Филиппа II, врага Генриха IV. Филипп II в конце концов заподозрил, что французский король заключил сделку с дьяволом, поскольку ему удавалось мгновенно угадывать все его дипломатические уловки, Виет достиг отличных результатов в геометрии и алгебре, продвинул вперед тригонометрию и решение уравнений. Возможно, важнейшим из его открытий является создание современного символического языка алгебры, который произвел революцию в математике и способствовал прогрессу в науке.
Его принципиальным соперником, а впоследствии другом был Адриан ван Роумен (1561–1615).
Виет предложил ему задачу о касающихся окружностях, известную как задача Аполлония.
В задаче Аполлония необходимо найти все окружности, касающиеся трех данных окружностей. По традиции, решение нужно было найти только с помощью циркуля и линейки.
* * *
Друг и соперник Виета, голландский геометр Адриан ван Роумен (1561–1615) бросил все силы на изучение метода Архимеда и, использовав многоугольники с огромным числом сторон, в 1593 году с точностью определил 16 десятичных знаков π.
Но огромный труд ван Роумена не сравнится с работой, которую проделал Аюдольф ван Цейлен (1540–1610). Этот немецкий математик был одержим идеей вычисления числа π. В 1596 году он нашел первые 20 знаков, позднее доведя число знаков до 35, которые стоит привести здесь:
π = 3,14159265358979323846264338327950288…
В общем случае эта задача имеет восемь различных решений.
Ван Цейлен получил такую известность, что во многих странах число π стало известно как лудольфово число. Свое любимое число ван Цейлен даже повелел высечь на своем надгробии в городе Лейден. К сожалению, во время Второй мировой войны его могила была разрушена. В главе 5 приведена иллюстрация, на которой изображена его могила с нанесенными на каменное надгробие знаками числа π, восстановленная в 2000 году. Упорные труды ван Цейлена заслуживают подобного памятника.
Виллеброрд Снелл (1580–1626), печатавшийся под латинизированным именем Снеллиус, прежде всего известен как первооткрыватель законов преломления света. Он также пробовал вычислить число π и рассчитал 35 его знаков, опубликованных в 1621 году в книге Cyclometricus. Он использовал ощутимо более точный способ по сравнению с методом Архимеда. Правильность расчетов Снелла позднее подтвердил великий Христиан Гюйгенс (1629–1695).
В 1630 году астроном Христоф Гринбергер (1561–1636), австрийский иезуит, установил новый рекорд, дойдя в расчетах до 39-го знака. Потомки достойно увековечили его память: его имя носит один из лунных кратеров. Нельзя представить лучшее вознаграждение для астронома и для того, чей сан священника не позволял принимать мирские подношения.
Готфрид Лейбниц и Исаак Ньютон обессмертили свои имена, создав анализ бесконечно малых величин — кошмар для многих студентов, видящих в этой дисциплине лишь нагромождение интегралов и производных. Лейбниц и Ньютон достигли математического рая: им удалось «приручить» бесконечность, более того, показать, как перейти от конечного к бесконечному и вернуться обратно, принеся с собой нужные результаты. Многие, подобно проницательному и мечтательному Архимеду, ступали на этот путь. Лейбниц и Ньютон смело прошли по нему и показали входы и выходы лабиринта, в котором скрывалось неизведанное.
Степенные ряды и интегралы — результат применения приемов анализа в математике. Расчет числа π перестал заключаться в механическом измерении многоугольников и стал математической задачей, требующей работы «маленьких серых клеточек», как говорил знаменитый сыщик Эркюль Пуаро.
Далее мы не будем упоминать об ученых Востока, занимавшихся вычислением π, за исключением случаев, когда им удавалось рассчитать π с крайне большой точностью или использовать оригинальные передовые методы.
ГОТФРИД ВИЛЬГЕЛЬМ ЛЕЙБНИЦ (1646–1716)
Коротко изложить самые важные достижения столь разностороннего ученого, как Лейбниц, далеко не просто. Достаточно упомянуть, что полное собрание его сочинений насчитывает 25 томов и 200000 страниц. Этот исключительный ученый родился в Лейпциге. Он занимался адвокатурой, дипломатией, математической логикой, религией, историографией, а также востоковедением, двоичной арифметикой, этикой, физикой, биологией, инженерным делом. Возможно, важнейшим его вкладом в науку является интегральное исчисление и анализ бесконечно малых.
Лейбниц был вундеркиндом, много читал и схватывал все на лету, жил, не стесняясь в средствах, зарабатывая юриспруденцией и дипломатией. Он участвовал в создании первого в истории научного журнала Acta Eruditorum, в котором публиковались многие, если не все его исследования и открытия.
Ему был присущ дар метко обозначать вещи. Так, именно ему мы обязаны введением знака интеграла и дифференциала (dх), а также многих выражений, например «жизненная сила». Часть его жизни прошла в спорах с приверженцами Ньютона (за которыми стоял сам великий Ньютон) о том, кто же является подлинным автором исчисления. Сегодня считается, что и Ньютон, и Лейбниц совершили свои открытия независимо друг от друга, а совпадение по времени является случайным. Как математик Лейбниц также внес очень важный вклад в математическую логику, теорию автоматов, двоичную систему счисления и топологию, которую сам ученый называл analysis situs.
В 1673 году Лейбниц изобрел счетную машину, способную производить четыре основных арифметических действия. Годом позже он построил первый работающий образец.
* * *
Ньютон и Лейбниц на протяжении долгого времени вели спор о том, кому же принадлежит авторство исчисления, и можно сказать, что этот спор в итоге вылился в скандал. Не будем вдаваться в суть спора и сосредоточимся на его итогах.
Около 1666 года, в разгар Великого Лондонского пожара сэр Исаак Ньютон, казалось, прохлаждался без работы, поскольку год спустя он говорил, что занялся вычислением числа π «оттого, что тогда мне было решительно нечем заняться». Оставим в стороне мотивы, которыми он руководствовался, и рассмотрим суть его расчетов. Ньютон использовал биномиальную формулу и открыл ряд
с помощью которого точно вычислил 16 знаков π. Как и во многих других случаях, Ньютон не придал этому большого значения и не упомянул об этом ни в одной из своих книг. Этот результат был опубликован после его смерти.
Следовать по пути гения всегда интересно. Проследуем путем, который прошел Ньютон.
Площадь выделенного на рисунке сектора равна π/24, так как он равен одной шестой части окружности. Если вычесть площадь треугольника, равную √(3/32), то получим площадь части сектора, обозначенной 5. Уравнение окружности, показанной на рисунке, выглядит так:
у2 + х2 = х,
СЭР ИСААК НЬЮТОН (1642–1727)
Ньютон больше известен как физик и математик, хотя он занимался алхимией, богословием, политикой, астрономией и, естественно, многими другими дисциплинами. В любом случае он является одним из важнейших ученых в истории человечества.
Его основной труд Philosophiae naturalis principia mathematica («Математические начала натуральной философии») был издан в 1687 году главным образом благодаря влиянию родных, что говорит о том, насколько замкнутым и необщительным был Ньютон. В этой книге описываются его важнейшие открытия: закон всемирного тяготения (по легенде, Ньютон открыл этот закон после того, как ему на голову упало яблоко) и исчисление бесконечно малых. Среди его достижений в физике в первую очередь стоит отметить создание теории цветов и дифракции, первого зеркального телескопа и корпускулярной теории света. Он также сформулировал законы сохранения импульса и энергии. В его работах по астрономии удивительно точно описано движение планет и природа их орбит. В чистой математике помимо дифференциального и интегрального исчисления он также изучал множество степенных рядов, формулу бинома, теорию ошибок и численный метод нахождения нулей функции.
Ньютон дважды избирался в парламент, где почти всегда хранил молчание. Единственным легендарным исключением стал случай, когда он попросил закрыть окно, потому что ему мешал сквозняк. Став в 1699 году управляющим Монетного двора и проведя много реформ, Ньютон лично отправил на виселицу нескольких фальшивомонетчиков. Он всегда считал, что его открытия в алхимии и богословии (Ньютон был наполовину монофизитом и сохранял в тайне принадлежность к этой еретической доктрине) переживут его. Ньютона практически обожествляли еще при жизни, а после смерти и похорон в Вестминстерском аббатстве на все восхваления, казалось, был наложен строгий запрет. Это объяснимо, если мы вспомним историю расправы над фальшивомонетчиками.
Исаак Ньютон на картине Уильяма Блейка (1757–1827). Величие ученого и его влияние на научный мир вдохновили Александра Поупа (1688–1744) написать такие строки:
Природы строй, ее закон
В извечной тьме таился.
И бог сказал: «Явись, Ньютон!»
И всюду свет разлился.
(Перевод А. П. Павлова)
* * *
что можно представить в виде у2 = х(1 — х) или у = √(x(1 — x)) = х1/2(1 — х)1/2 Применив методы интегрального исчисления, изобретенного самим Ньютоном, получим:
Теперь осталось лишь правильно выполнить интегрирование и не ошибиться в расчетах… либо нужно быть Ньютоном.
Его соотечественник Абрахам Шарп (1651–1742) использовал следующее равенство, полученное астрономом Эдмундом Галлеем (1656–1742):
π/6 = arctg(√3/3)
которое сегодня изучается в элементарной тригонометрии, а также важное соотношение, полученное еще одним британским ученым Джеймсом Грегори (1638–1675):
arctg x = x — (x3/3) + (x5/5) — …
и получил ряд, который на современном языке математики записывается так:
что в 1699 году позволило ему правильно вычислить 71 знак π. На самом деле Шарп рассчитал 72 знака, но ошибся в последнем. Это простительно, если учесть, что для этого пришлось сложить около 300 членов указанного ряда.
Заметим также, что в 1667 году Джеймс Грегори попытался доказать, что задача о квадратуре круга не имеет решения, но потерпел неудачу.
Несколько лет спустя, в 1706 году, Джон Мэчин (ок. 1686–1751), преподаватель астрономии, позднее ставший секретарем Лондонского королевского общества, вывел формулу, носящую теперь его имя:
π/4 = 4∙arctg (1/5) — arctg (1/239)
* * *
ДЖЕЙМС ГРЕГОРИ (1638–1675)
Не следует пугать Джеймса Грегори с его племянником Дэвидом Грегори (1659–1708), который также был математиком, дружил с Ньютоном и был одним из тех, кто ввел в употребление символ π, Джеймс Грегори известен в астрономии как изобретатель телескопа-рефлектора, а также благодаря разложению в бесконечные ряды тригонометрических функций (sin x, cos x, tg x) и обратных тригонометрических функций (arcsin х, arccos x и arctg x). Ряд, который был открыт также и Мадхавой из Сангамаграма и носит имя Мадхавы-Лейбница или Грегори-Лейбница, может быть записан в следующем виде:
Этот ряд сходится на интервале от — π/4 до π/4. Грегори одним из первых понял, что задача о квадратуре круга нерешаема.
Чтобы получить эту формулу, он выполнил следующие действия:
tg α = 1/5,
tg 2α = 2∙tg α/(1 — tg2 α) = 5/12,
tg 4α = 2∙tg 2α/(1 — tg2 2α) = 120/119,
tg (4α — π/4) = (tg 4α — 1)/(1 + tg 4α) = 1/239.
Отсюда следует искомое равенство, так как
4α — π/4 = arctg tg (4α — π/4) = arctg 1/239.
Ha основе этой формулы вкупе с известными выражениями, например
arctg (x) = x — (x3/3) + (x5/5) — …
выводятся быстро сходящиеся ряды, с помощью которых Мэчин рассчитал π до сотого знака. Вне всякого сомнения, большой заслугой Мэчина является полученная им формула, записываемая в тригонометрическом виде, которую можно быстро преобразовать в ряд. Далее, когда мы будем рассказывать о Захариусе Дазе, то упомянем еще один любопытный факт, имеющий отношение к Мэчину.
Формулы, подобные той, что вывел Мэчин (так называемые формулы Мэчина), очень распространены, их изучением занимались многие исследователи независимо друг от друга. Мэчин стал первым среди них.
В девятом томе первого издания Французской энциклопедии, созданной силами Дени Дидро, упоминается Том Фанте де Ланьи (1660–1734), преподаватель гидрографии и математики, чей некролог редактировал сам Фонтенель. В 1719 году де Ланьи вычислил (сущая безделица!) 112 знаков π, использовав тот же степенной ряд, что и Шарп.
ЗАДАЧА, ПЕРЕД КОТОРОЙ НЕЛЬЗЯ УСТОЯТЬ
Математик Том Фанте де Ланьи (1660–1734), родившийся во французском городе Лионе; занял свое, пусть скромное, место в истории благодаря тому, что первым верно вычислил 112 знаков числа π — абсолютный мировой рекорд в то время. С ним также связан занимательный эпизод, произошедший незадолго до его смерти. Рассказывают, что его коллега Мопертюи пришел навестить его на смертном одре и обнаружил тело без признаков жизни. Чтобы удостовериться в этом, Мопертюи еле слышно прошептал: «Сколько будет 12 в квадрате?», предполагая, что ни один математик не устоит перед подобной задачей. Де Ланьи вскочил, громко воскликнул: *144!* — и умер.
* * *
На самом деле де Ланьи вычислил 127 знаков, но лишь 112 из них были верными, что подтвердил Георг Вега (1754–1802). Этот немецкий математик к концу жизни был удостоен высокого титула барона в Австрийской империи, что не спасло его от судьбы простолюдина: он был убит неким вором из-за денег и часов. В 1794 году Вега использовал одну из формул Мэчина, которую вывел Эйлер, чтобы вычислить 137 знаков π, на этот раз без ошибок. Он использовал следующую формулу:
π/4 = 5∙arctg (1/7) + 2∙arctg (3/79).
Банкнота в 50 словенских толаров, на которой изображен Гэорг Вега, а также геометрические построения и фазы Луны. На обороте слева от изображения Солнечной системы можно увидеть фасад Словенской академии наук в Любляне.
Между 1760 и 1800 годами параллельно были получены заслуживающие упоминания результаты. Так, Иоганн Генрих Ламберт (1728–1777), создатель неевклидовой геометрии, в 1761 или 1767 году (точная дата неизвестна) доказал иррациональность числа π. Адриен Мари Лежандр (1752–1833) несколькими годами позже показал, что π2 также иррационально. Возможно, наиболее значимым является достижение великого Леонарда Эйлера (1707–1783), который искал многочисленные ряды для вычисления π и предположил, что число π является трансцендентным. Гипотеза Эйлера тем примечательнее, что само существование трансцендентных чисел доказал Жозеф Лиувилль (1809–1882) лишь много лет спустя, в 1840 году! Лиувилль также нашел первое трансцендентное число.
ИОГАНН ГЕНРИХ ЛАМБЕРТ (1728–1777)
Этот немецкий математик, астроном и врач изобрел гигрометр и фотометр. Он также первым доказал иррациональность числа тс, но этим его вклад в математику не ограничивается. Он изучал гиперболические функции и связал их с неевклидовой геометрией. Также он внес заметный вклад в картографию, и его имя носит одна из географических проекций. Ламберт был самоучкой, но когда речь заходила о признании его собственных заслуг, скромность покидала его. Фридрих II, сделав математика членом Прусской академии наук, спросил Ламберта, в каких же науках он преуспел. «Во всех», — последовал ответ, близкий к истине. Король с иронией заметил: «Значит, вы разбираетесь и в математике?» — «И в ней тоже», — честно ответил Ламберт. Несколько раздосадованный, Фридрих II продолжил: «И кто же был вашим учителем?» — «Я сам, Ваше Величество!» — и снова Ламберт не погрешил против истины. Король иронично сказал: «Ну и ну! Я стою перед вторым Паскалем!» — «По меньшей мере», — был ответ. Его доказательство иррациональности числа тс достаточно изобретательно и доступно для понимания. С помощью цепных дробей Ламберт показал (это наиболее сложная часть его доказательства), что если х — ненулевое рациональное число, то tg х иррационально. Так как tg π/4 = 1, а единица является рациональным числом, следовательно, π/4 и π являются иррациональными.
* * *
Говоря о вычислении π, мы специально не упоминаем об Эйлере, так как он никогда не добивался рекордной точности вычислений. Вероятно, это случилось лишь потому, что он не уделял этому достаточно внимания: как-то раз, используя формулы Мэчина, он вычислил 20 знаков π всего за час!
В 1841 году Уильям Резерфорд (1798–1871) использовал формулу Мэчина
π/4 = 4∙arctg (1/5) — arctg (1/79) + arctg (1/99).
и получил 208 знаков π, из которых 152 были верными. В 1853 году он вернулся к этой задаче и с помощью формулы Мэчина установил новый рекорд — 440 знаков.
ЧТО ТАКОЕ ТРАНСЦЕНДЕНТНОЕ ЧИСЛО?
Число называется алгебраическим, если оно является корнем многочлена
anxn + an-1xn-1 +… + a1x + a0
все коэффициенты которого аn, аn-1…., a1, а0 являются рациональными числами. В высшей математике доказывается, что любое число, которое можно получить, используя лишь циркуль и линейку конечное число раз, обязательно является алгебраическим. Неалгебраическое число называется трансцендентным. Таким образом» очевидно, что трансцендентное число нельзя получить построением с помощью циркуля и линейки.
* * *
Иоганн Мартин Захариус Дазе (1824–1861) занимает особое место в истории математики. Его друг Шульц фон Штрасницкий (1803–1852) показал ему следующую формулу Мэчина:
π/4 = arctg (1/2) + arctg (1/5) + arctg (1/8).
и в 1844 году Дазе вычислил с ее помощью 200 знаков π. Невероятно, но на это ему потребовалось лишь два месяца, и все расчеты он производил в уме. Он был настоящим человеком-компьютером и обладал невероятной способностью к вычислениям. Сам Гаусс, известнейший математик своего времени, советовал властям использовать Дазе для расчетов. Была учреждена премия, вручаемая тому, кто получит список делителей чисел N таких, что 7 000 000 < N < 10 000 000. Дазе начал работать над этой задачей, но смерть помешала ему найти решение. Дазе страдал синдромом саванта: он был поразительно одарен в математике, имел невероятную память, но в остальном был весьма и весьма средних способностей. Например, он мог перемножить два восьмизначных числа меньше чем за минуту. Для перемножения 100-значных чисел ему требовалось около девяти часов. Он обладал почти фотографической памятью, что позволяло ему с удивительной точностью пересчитывать любые предметы, будь то овцы, буквы или костяшки домино. Писатель и ученый Артур Кларк в письме к палеонтологу Стивену Джею Гулду задавался вопросом, какую пользу для эволюции биологического вида может иметь способность вычислить в уме 200 знаков числа π. Ответ на этот вопрос нам неизвестен.
В 1847 году датский астроном и математик-самоучка Томас Клаусен (1801–1885), используя две формулы Мэчина:
(1/4)∙π = 2∙arctg (1/3) + arctg (1/7),
(1/4)∙π = 4∙arctg (1/5) — arctg (1/239).
точно вычислил 248 знаков Я. Он также ошибся в вычислениях, но допустил ошибку в самом конце расчетов, всего вычислив 250 знаков.
В 1853 году его немецкий коллега Якоб Гейнрих Вильхельм Леманн (1800–1863) рассчитал 261 знак Я, что принесло ему известность в математике. Его именем также назван кратер на Луне. В следующем году немецкий профессор Рихтер вычислил 330, затем 400 и, наконец, 500 знаков.
Английский математик-любитель Уильям Шэнкс (1812–1882) посвятил свою жизнь вычислениям. Наряду с расчетами других констант в 1875 году он получил 707 знаков π, что увековечено на знаменитом фризе Дворца открытий в Париже. Но это стоило музею немалых затрат: фриз был построен в 1937 году, а в 1946 году Дэниел Фергюсон в статье в журнале Nature показал, что верными являются лишь первые 527 знаков. Огастеса де Моргана (1806–1871) крайне удивил тот факт, что цифра 7 встречается в записи числа π заметно чаще остальных.
Подобно многим ученым, занимавшимся объемными расчетами, Шэнкс допускал ошибки. Он не располагал правильным ответом, с которым можно было бы свериться, поэтому считал свои вычисления верными. Не стоит забывать, что в те времена не было ни компьютеров, ни калькуляторов, все расчеты выполнялись на листах бумаги, испещренных бесчисленными цифрами. Теперь во Дворце открытий можно посмотреть на исправленное значение π. Такова дань уважения объяснимой человеческой ошибке. В наши дни было обнаружено, где именно ошибся Шэнкс, который вычислял π поэтапно.
Не стоит умалчивать о достижении Фергюсона — последнего, о котором мы расскажем, прежде чем перейдем к повествованию о компьютерной эре. В 1947 году он опубликовал 808 знаков π. Для расчетов ему понадобился целый год, арифмометр, много терпения и следующая формула:
π/4 = 3∙arctg (1/4) + arctg (1/20) + arctg (1/1985)
В 1882 году немецкий математик фон Линдеман изрядно охладил пыл тех, кто занимался расчетами числа π, доказав, что оно не является алгебраическим, поэтому не может быть найдено построением с помощью циркуля и линейки. Линдеман доказал трансцендентность числа π. Следует отметить, что в его объемном доказательстве ни разу не использовались геометрические методы. Таким образом, число π покинуло мир геометрии, и это произошло точно в тот день, когда была доказана его трансцендентность.
Оригинальное доказательство Линдемана основано на тех же примерах, которые за несколько лет до того использовал Шарль Эрмит (1822–1901) для доказательства трансцендентности числа е — еще одной известной константы. Линдеман пришел к выводу, что линейная комбинация степеней е с коэффициентами Ak и показателями степени Bk (вещественными или комплексными)
А1ев1 + А2ев2 + … + Аnевn
не может быть равной нулю (за исключением случая, когда все коэффициенты нулевые). Так как знаменитая формула Эйлера может быть записана в следующем виде:
eπi + 1 = eπi + e0 = 0,
она удовлетворяет условиям Линдемана (А1 = A2 = 1, B1 = πi, В2 = 0), поэтому πi не может являться алгебраическим числом, равно как и само π. Число π не является алгебраическим, следовательно, оно трансцендентно. Так как оно трансцендентно, его нельзя получить построением с помощью циркуля и линейки. Конечно, за этим последовали новые, менее сложные доказательства, но и приведенных выкладок было достаточно, чтобы снять завесу тайны с числа π. До Линдемана было известно, что трансцендентность числа π означает, что задача о квадратуре круга нерешаема. Доказательство Линдемана положило конец поискам решения этой легендарной задачи. Было окончательно установлено: задача о квадратуре круга не имеет решения.
 ТЕЛЕГРАМ
ТЕЛЕГРАМ Книжный Вестник
Книжный Вестник Поиск книг
Поиск книг Любовные романы
Любовные романы Саморазвитие
Саморазвитие Детективы
Детективы Фантастика
Фантастика Классика
Классика ВКОНТАКТЕ
ВКОНТАКТЕ