Секреты числа пи [Почему неразрешима задача о квадратуре круга] (Мир математики. т.7.)

Глава 4 Формулы с числом π

Лорд Кельвин как-то написал на доске формулу

и, обращаясь к слушателям, сказал: «Математик — это тот, для кого эта формула столь же очевидна, как 2 + 2 = 4».

Мы не будем заходить так далеко, как лорд Кельвин, но все же приведем несколько формул, в которых используется π. Присутствие формулы в тексте гарантирует, что не слишком заинтересованный читатель непременно отвлечется, поэтому мы постарались использовать как можно меньше формул и объединить их в одной главе.

Некоторые из них обязательно знать всем, кто интересуется этой темой, поэтому их нельзя было не включить в эту главу. Более сложные формулы будет непросто понять, но с ними следует ознакомиться, чтобы осознать, каких усилий стоило открыть их.

Выражения, в которых используется π, полезно знать. Те, что касаются физики, порой столь же интересны, сколь трудны для понимания.

Формула ниже — это закон Кулона, описывающий силу взаимодействия между двумя зарядами q₁ и q₂, расположенными на расстоянии r, где ε₀ — электрическая постоянная:

F = |q₁q₂|/4πε₀r²

Это третий закон Кеплера, где Р — период обращения планеты вокруг Солнца, m₁ и m₂ — масса Солнца и планеты, а — большая полуось орбиты, G — гравитационная постоянная:

p² = [4π²/G(m₁ +m₂)]∙a³

Принцип неопределенности Гейзенберга для частицы со средним значением координаты х и средним импульсом р, где h — нередуцированная постоянная Планка:

ΔxΔy >= h/4π

Космологическая константа, где G — гравитационная постоянная, с — скорость света, р — плотность материи и излучения:

= (8πG/3c²)∙p.

Можно предположить, что следующие формулы будут интересны только специалистам, поэтому мы не будем продолжать. Стоит отметить, что эти и другие физические формулы не используются для расчетов Я, но их полезно знать каждому образованному человеку.

Простейшие формулы прежде всего относятся к так называемым коническим сечениям — кривым, получаемым в результате рассечения конуса плоскостью. В следующих формулах r обозначает радиус.

Длина окружности:

L = 2πг.

Площадь круга:

S = πr².

Площадь эллипса с полуосями а и Ь:

S = πаЬ.

Площадь правильного многоугольника с n сторонами и длиной стороны а:

S = (1/4)∙na²ctg (π/n)

Площадь поверхности сферы:

S = 4πr²

Общая площадь поверхности цилиндра с высотой h:

S = 2πr∙(r + h).

Общая площадь поверхности конуса с образующей g:

S = πr∙(r + g).

Объем сферы:

V = (4/3)∙πr³.

Объем эллипсоида с полуосями а, Ь и с:

V = (4/3)∙πabc

Объем цилиндра с высотой h:

V = πr²h.

Объем конуса с высотой h:

V = πr²h/3.

Также, разумеется, существуют и другие формулы, в которых используется π и очень сложные интегралы.

Под простой формулой будем понимать любую формулу, найденную до наступления компьютерной эры. С наступлением эпохи компьютеров математики сосредоточили внимание на вычислении знаков π с наибольшей эффективностью. Красота расчетов уступила место эффективности вычислений. Простое перечисление формул будет достаточно громоздким, но у нас не остается другого выхода:

В последней формуле использован круговой интеграл. Предполагается, что обход дуги окружности осуществляется против часовой стрелки.

Важное место среди математических формул с числом π занимают ряды:

Подобные ряды могут иметь и такой вид:

Существуют также ряды, связывающие π и загадочную дзета-функцию Римана ζ (s):

В последнем случае В_2n — числа Бернулли, изучаемые в высшей математике. Для справки приведем первые несколько чисел Бернулли:

Возможно, перечисление рядов — не совсем то, чего ожидал читатель. Рассмотрим подробнее простой пример: первый ряд из нашего списка, именуемый формулой Лейбница. Рассмотрим ряд

1/(1 + x²) = 1 — x² + x⁴ — x⁶ + x⁸ — …,

сходящийся при |х| < 1. Можно проинтегрировать его почленно и использовать интегральное исчисление для расчетов:

Приняв х = 1, увидим, что доказательство близится к завершению. Чтобы подтвердить правильность полученного результата для х = 1, учитывая, что этот результат верен для |х| < 1, нужно выполнить еще несколько действий. Запишем исходный ряд, но остановимся на (n — 1) — м члене, записав остаток так, как если бы речь шла об n-м члене:

Проинтегрировав почленно от 0 до 1 и приняв х = 1, имеем

При переходе к пределу при n —> оо последний член стремится к нулю. Следовательно,

actg 1 = π/4 = 1–1/3 + 1/5 — 1/7 + 1/9 — …

К сожалению, этот ряд не слишком удобен для расчетов π, так как он сходится слишком медленно. Чтобы получить десять знаков π, нужно найти сумму 10⁵⁰ членов ряда — число поистине астрономическое. Из очевидных соображений мы не будем повторять эти действия для всех ранее приведенных рядов. Это было бы слишком трудоемко, но мы не получили бы никаких новых результатов. Следующий ряд иногда называют рядом Грегори-Лейбница. В действительности его нужно было бы именовать рядом Мадхавы из Сангамаграма, так как именно этот индийский математик первым открыл формулу. Этот ряд записывается так:

где F_n — это числа Фибоначчи, элементы числовой последовательности, в которой каждое число является суммой двух предыдущих:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144….

Также π фигурирует в так называемых бесконечных произведениях. Следующую формулу вывел Джон Валлис (1616–1703):

Ее можно свести к интегралу

путем трудоемких математических преобразований. Лорд Броункер (1620–1684) преобразовал эту формулу в цепную дробь.

Авторство следующего бесконечного произведения принадлежит Эйлеру:

Оно имеет особенность: в нем используются только простые числа, как и в другом бесконечном произведении, еще более необычном:

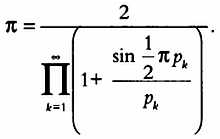
Здесь используются простые числа p_k вкупе с тригонометрическими функциями. Воображение Эйлера поистине не знало пределов.

* * *

Классический результат, приведенный ниже, принадлежит французскому математику Франсуа Виету (1540–1603):

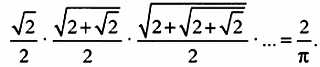
Это произведение, само по себе красивое с точки зрения математики, можно преобразовать в еще более прекрасное выражение, что сделал Хоаким Мунхаммар в 2000 году:

Число пар кроликов F_n в поколении n при отсутствии смертей и при условии, что первая пара кроликов в первом поколении не размножается, подчиняется правилу F_n = F_n-1 + F_n-2ⁿ

F_n называются числами Фибоначчи.

* * *

Вывод формулы Виета на современном языке выглядит следующим образом. Будем использовать треугольник, который применял еще Архимед. Обозначим основание треугольника за Ь, угол, образованный высотой h и стороной треугольника, за ОС.

Имеем

S_n = n ∙ площадь треугольника.

Используя элементарную тригонометрию (в развитие которой сам Виет внес заметный вклад), получим:

S_n = (1/2)∙nr²∙sin 2α = nr²∙sin α∙cos α.

Следуя по пути Архимеда и используя многоугольник с удвоенным числом сторон, имеем

S_2n = (1/2)∙2∙nr²∙sin 2α = nr²∙sin α.

Тогда

S_n/S_2n = cos α

Это ключевой момент рассуждений, поскольку далее с помощью простых алгебраических преобразований выводится следующее выражение:

Заметим, что при переходе к пределу при k —» oo

После еще одного элементарного преобразования имеем

что сводится к исходной формуле. Как оценить начальное значение α? Если, подобно Виету, взять в качестве исходного многоугольника квадрат, где

n = 4, cos α = √(1/2),

и использовать тригонометрическую формулу половинного угла, согласно которой

cos (χ/2) = √[(1/2) + (1/2)∙cos χ]

получим, пусть и другим способом, искомое выражение:

Не будем забывать, что Виету нельзя было отказать в изобретательности. Отдельное место занимают две формулы, которые считаются королевами математической красоты. Они известны как формула Эйлера:

e^π' + 1 = 0

и формула Стирлинга:

n! ~ √(2πn)∙(n/e)''.

Если говорить о цепных дробях, то с их помощью π выражается весьма непросто (первым с помощью бесконечной дроби значение π вычислил Ламберт):

Существуют и другие дроби, не столь известные, но намного более симметричные:

Последняя из формул — это формула лорда Броункера в несколько измененном виде. Цепные дроби отличаются одним положительным свойством: стоит нам остановиться в вычислениях на каком-либо этапе, полученная дробь будет наилучшим из возможных приближенных значений искомого числа. Если при вычислении π с помощью цепной дроби мы остановимся на определенном этапе и «раскрутим» этот клубок в обратную сторону, получим наилучшее из возможных приближенных рациональных значений. Так, если мы остановимся на дроби [3; 7, 15], то получим

* * *

Дробь 333/106 является наилучшим рациональным приближенным значением: чтобы получить любое более точное значение, будет необходимо увеличивать знаменатель. Приближенное значение π = 333/106 в свое время получил Ривар, причем погрешность этого значения крайне мала.

Из так называемой формулы Мэчина

π/4 = 4∙arctg (1/5) — arctg (1/239)

были выведены другие формулы, которые применялись для вычисления знаков π. Позднее мы приведем две подобные формулы, которые использовал японский специалист Канада при расчетах 1241100 000 000 знаков π.

Индийский математик Рамануджан примерно в 1910 году получил первую из этих формул (и еще 16 подобных ей):

Эта формула отличается удивительным свойством: с вычислением каждого последующего члена она дает 8 новых десятичных знаков π. Однако для доказательства этой формулы пришлось подождать три четверти столетия, так как Рамануджан не потрудился привести доказательство. Билл Госпер, один из первых хакеров в истории, использовал эту формулу для расчета 17 миллионов знаков π. Вариант

позволил находить не 8, а 14 знаков на каждом шаге вычислений. Помимо этого, вычисления стало возможным разделить между несколькими компьютерами.

Приведенная формула была получена братьями Чудновскими в 1987 году. Мы приводим ее, чтобы подчеркнуть, насколько быстро развивается все, связанное с информатикой: в XXI веке эту формулу используют для расчетов на персональных компьютерах, а не суперкомпьютерах.

Эти формулы могут показаться сложными, что не помешало им появиться в фильме «Классный мюзикл» (High School Musical): в одной из сцен они написаны на доске, причем одна формула содержит ошибку, которую исправляют прямо по ходу действия. В чувстве юмора сценаристам не откажешь.

В 1946 году с появлением ENIAC (сокр. от Electronic Numerical Integrator and Computer — электронный числовой интегратор и вычислитель) в вычислениях начали использоваться компьютеры, и все, в том числе расчет знаков π, изменилось навсегда. ENIAC был первым электронным компьютером, предназначенным исключительно для вычислений. Его ближайшим предком была ЭВМ «Колосс», использованная Аланом Тьюрингом (1912–1954) в Блетчли-парке в военных целях, а именно для расшифровки секретных сообщений немцев. ENIAC разработали Джон Пресперт Экерт (1919–1995) и Джон Уильям Мокли (1907–1980). Этот компьютер обладал колоссальными размерами и потреблял неимоверное количество электроэнергии: в нем насчитывалось почти 100000 резисторов, реле, диодов, вакуумных ламп, конденсаторов и т. д. Его вес превышал 27 тонн, а длина составляла свыше 30 метров. ENIAC выделял столько тепла, что помещение прогревалось почти до 50 °C. Этот гигант совершал 5000 операций сложения в секунду — в тысячу раз больше, чем его предшественники (ив несколько тысяч раз меньше, чем современные персональные компьютеры). Кроме этого, он мог хранить в памяти 200 цифр. ENIAC программировался с помощью множества штекеров, подобно старинным телефонным станциям. Он был столь огромен потому, что в то время не существовало ни транзисторов, ни микросхем. В нем также не использовалась современная архитектура фон Неймана, в соответствии с которой данные и программы хранятся в одной и той же памяти.

* * *

Вычисление первых 2037 знаков π на компьютере ENIAC заняло 70 часов. В таблице ниже указано рассчитанное количество знаков π и год, чтобы дать представление о том, какие изменения вызвало появление компьютеров:

В 1973 году старинная формула Эйлера вкупе с формулой Мэчина позволила Гийу и Буйе вычислить миллион знаков π:

Любопытно, что для вычисления второго слагаемого достаточно вычислить первое и перенести запятую на несколько позиций. Вне зависимости от их абсолютной величины два первых слагаемых будут отличаться только количеством нулей.

В 1976 году Юджин Саламин и Ричард Брент предложили алгоритм, основанный на давней гипотезе Гаусса и Лежандра о последовательном вычислении средних арифметических и средних геометрических. Суть алгоритма непросто описать вкратце. Алгебраический алгоритм — это метод расчета некой величины, в данном случае Я. Саламин и Брент использовали следующие исходные равенства:

a₀ = 1; b₀ = 1/√2; t₀ = 1/4; p₀ = 1,

затем рекуррентным способом вычислили

a_n+1 = (a_n + b_n)/2;

b_n+1 = √(a_nb_n);

t_n+1 = t_n — p_n(a_n - a_n + 1)²;

p_n+1 = 2p_n.

В пределе справедливо следующее соотношение:

π ~ (a_n + b_n)²/4t_n.

Этот алгоритм, который было бы невозможно использовать без помощи компьютера, обладает квадратичной скоростью сходимости, то есть на каждом шаге число знаков, полученное на предыдущем, удваивается. С использованием этого алгоритма было получено 206158430000 знаков π.

Но и это еще не все: в 1980-е годы Петер и Джонатан Борвейны создали алгоритм со скоростью сходимости четвертой степени, с помощью которого было рассчитано 1241100 000 000 знаков. Мы не станем приводить его здесь, так как он будет понятен лишь узким специалистам.

* * *

В конце 2002 года группа японских специалистов, возглавляемая Ясумасой Канадой, достигла результата, который теперь уже не так удивляет научный мир. Тем не менее последняя страница в этой истории еще не написана. Прогресс в этой области, кажется, не прекращается: в 2011 году был получен 10 000 000 000 050 знак числа π.

Сколь далек этот результат от предсказания Дэниела Шенкса (не путать с Уильямом Шенксом), который в 1983 году заявил, что вычисление миллиарда знаков π станет неприступной задачей! Сохраним для истории две формулы Мэчина, которые использовал Канада:

π/4 = 12∙arctg (1/49) + 32∙arctg (1/57) — 5∙arctg (1/239) + 12∙arctg (1/110443)'

π/4 = 44∙arctg (1/57) + 7∙arctg (1/239) — 12∙arctg (682) + 24∙arctg (1/12943).

Первая формула была открыта в 1982 году, а вторая была найдена Фредериком Карлом Штермером еще в 1896 году (опубликована в журнале Французского математического общества). Кто бы мог подумать, что эта формула будет использована для подобной задачи спустя столько лет! В математике никогда нельзя загадывать наперед: то, что сегодня кажется несущественным, завтра может стать основополагающим.

Возможно, помимо рекордных вычислений читателя заинтересуют не совсем традиционные вычислительные методы. Применение формулы

позволяет вычислить любой n-й знак π без необходимости рассчитывать все предыдущие. Увы, но результатом является только двоичное или шестнадцатеричное число. Формулы, подобные этой, создали Дэвид Бэйли, Питер Борвейн и Симон Плуфф. Они известны как формулы ВВР (по первым буквам фамилий их создателей). Считается, что эти формулы указывают на наступление новой эпохи в вычислениях.

Формула Фабриса Беллара (род. в 1972 году)

является производной от формул ВВР, и с ее помощью вычисления выполняются на 43 % быстрее.

При расчетах в двоичной системе находятся значения битов (0 или 1). Уже вычислен квадриллион знаков числа π. Используя эту формулу, мы можем определить, находится ли на определенной позиции 0 (возможны лишь два варианта: 0 или 1), не зная при этом предшествующих знаков. Совершенству нет предела, хотя реальная полезность подобной формулы представляется сомнительной.

В заключение упомянем, что уже найдены формулы, с помощью которых можно найти произвольный знак π в любой системе счисления.

В завершение этой главы приведем еще несколько любопытных примеров. Например, формула

iⁱ = e^-π/2

объединяет комплексные и вещественные числа.

Следующее равенство связывает π с простыми числами:

где

ф(k) — количество целых чисел, меньших k и взаимно простых с ним.

Следующая формула касается квазицелых чисел. Эти числа очевидно являются иррациональными, но при расчетах на обычном калькуляторе выглядят как целые. Эти числа начинают отличаться от «реальных» целых чисел спустя множество знаков после запятой, и нужен очень точный калькулятор, чтобы увидеть этот десятичный знак после запятой, которому предшествует множество нулей. Выражение справа является квазицелым числом 427:

При расчетах на обычном калькуляторе значение этого выражения равно 427. Более точные расчеты показывают, что это число отличается от целого числа 427 только с 52-го знака после запятой. Именно с этого знака в десятичной записи этой дроби перестают фигурировать только нули. Выражение в скобках действительно заслуживает название квазицелого.

Нельзя отрицать, что π встречается во множестве областей. Например, рассмотрим гипотезу Кеплера об упаковке, чрезвычайно далекую от числа π. Какова максимальная плотность упаковки дисков на плоскости? Она равна

π/(2√3)