Жемчужина Эйлера

Глава 13 Планарные графы, математические планшеты и брюссельская капуста

В предыдущей главе мы видели, какую остроумную технику применил Коши для доказательства формулы Эйлера. Он взял многогранник, удалил одну грань и спроецировал все, что осталось, на плоскость этой грани. Затем он доказал, что для получившегося многоугольника имеет место формула V — E + F = 1, а значит, для исходного многогранника — формула V — E + F = 2. Связь с теорией графов бросается в глаза. На первый взгляд кажется, что было бы тривиально обобщить формулу Эйлера на графы, которые не являются проекциями многогранников и имеют криволинейные ребра.

Но трудность обобщения формулы Эйлера состоит в том, что это проходит не для всех графов. Подсчитать вершины и ребра просто — это те элементы, из которых граф и состоит, но вот граней у графа может и не быть. Даже в том случае, когда граф нарисован на бумаге, ребра необязательно разбивают область на грани. Например, ребро PR в левом графе на рис. 13.1 пересекает ребро QS, поэтому не может быть границей никакой грани. Однако этот граф можно нарисовать по-другому (как в правой части), так что пересечений не будет, и тогда область разбивается на грани. Граф, который можно нарисовать, так что ребра не пересекаются, называется планарным.

В многограннике грань — это область, ограниченная многоугольником. Для графов определение не такое строгое. Грань может быть ограничена одним ребром, как петля из P в P на рис. 13.1. Или двумя ребрами, как в случае пары ребер, соединяющих вершины Q и R. (Два ребра между одной и той же парой вершин называются параллельными.) Возможно даже, что ребро заходит внутрь грани, как ребро между S и T.

Рис. 13.1. Два представления одного и того же графа

Многие специалисты по теории графов считают внешнюю область гранью. Если рассматривать граф как остров, то эта неограниченная грань будет морем, протянувшимся в бесконечность во всех направлениях. И хотя называть эту неограниченную область гранью довольно странно, часто полезнее включать ее в число граней, чем исключать. Один из способов обрести душевный покой в этом вопросе — рассматривать граф как остров не в бескрайнем море, а на глобусе (рис. 13.2). Тогда неограниченная грань оказывается конечной.

Рис. 13.2. Расположение планарного графа на сфере

Итак, мы имеем следующее обобщение формулы Эйлера для планарных графов.

Если не считать неограниченную область гранью, то формула Эйлера принимает вид V — E + F = 1. У графа на рис. 13.1 пять вершин, семь ребер и четыре грани, 5–7 + 4 = 2, как и должно быть.

В качестве элементарного примера рассмотрим дерево. Деревом называется связный граф без циклов (см. рис. 13.3). Поскольку в дереве нет циклов, не ограничена всего одна грань, поэтому формула Эйлера дает V — E + 1 = 2, или V = E + 1. Иными словами, число вершин дерева на единицу больше числа ребер. В дереве на рис. 13.3 имеется 19 вершин и 18 ребер.

Рис. 13.3. Дерево

Существует много доказательств формулы Эйлера для графов. Мы приведем короткое, в котором, как и Коши, будем удалять ребра по одному. Но при этом будем осторожны, чтобы не повторить его ошибки.

Начнем с произвольного связного планарного графа. Выберем любое ребро. Это ребро либо соединяет две разные вершины, либо является петлей, которая начинается и заканчивается в одной и той же вершине. Предположим, что оно соединяет две вершины. Тогда будем стягивать ребро, пока оно не исчезнет полностью и два его конца не сольются в один. Это можно сделать так, что результирующий граф останется планарным (см. стягивание ребер a, c и d на рис. 13.4). Такая процедура уменьшает количество ребер и вершин на единицу, а число граней оставляет тем же самым. Поэтому величина V — E + F не изменяется. Теперь предположим, что ребро является петлей. В этом случае просто удалим ребро из графа (см. удаление ребер b и e на рис. 13.4). При этом число ребер и граней уменьшается на единицу, а число вершин остается неизменным. Поэтому величина V — E + F не изменяется.

Рис. 13.4. Сведение планарного графа к одной вершине путем удаления ребер a, b, c, d и, наконец, e

Продолжим процесс удаления ребер, пока не останется единственная вершина. В этот момент мы имеем одну вершину, ни одного ребра и одну грань (внешняя область). Поэтому V — E + F = 2. Поскольку величина V — E + F не изменялась на протяжении всего процесса, то V — E + F = 2 и для исходного графа.

У этой формулы есть интересное следствие: в любом представлении планарного графа с E ребрами и V вершинами количество граней одинаково. Иными словами, если десять человек нарисуют планарный граф, поставив точки там, где пожелают, и проведя ребра, так чтобы они не пересекались, то у всех графов будет одно и то же число граней (F = 1 + E — V, если не считать неограниченной грани). Например, на рис. 13.5 показан граф с четырьмя вершинами и шестью ребрами и два его планарных представления с тремя гранями каждое.

Рис. 13.5. Два разных планарных представления одного графа будут иметь одно и то же число граней

Поскольку формула Эйлера применима только к планарным графам, часто она используется для доказательства того, что граф не планарный. Для иллюстрации этой идеи введем два важных семейства графов: полные графы и полные двудольные графы.

В полном графе с n вершинами, обозначаемом K_n, n вершин, и каждая пара вершин соединена ровно одним ребром. Это самый большой возможный граф с n вершинами, не имеющий ни петель, ни параллельных ребер. Графы K₁… K₅ показаны на рис. 13.6. Удалив петли из графа домино (рис. 11.11), мы получили бы граф K₇.

Рис. 13.6. Полные графы K₁, K₂, K₃, K₄ и K₅

С полным графом тесно связан полный двудольный граф. Он обладает тем свойством, что множество вершин можно разделить на два подмножества U и V, так что никакие две вершины, принадлежащие U, и никакие две вершины, принадлежащие V, не соединены ребром, а каждая вершина из U соединена с каждой вершиной из V ровно одним ребром. Если U содержит m вершин, а V— n вершин, то соответствующий полный двудольный граф обозначается K_m,n. Графы K_3,2 и K_3,3 показаны на рис. 13.7. Типичный пример полного двудольного графа, который приводится в любом начальном учебнике по теории графов, — граф ресурсоснабжающих компаний. Множество U состоит из компаний (газовой, водопроводной, электрической и т. д.), а множество V — из клиентов. Поскольку каждый клиент должен получать ресурсы каждого вида, то получающийся граф полный двудольный.

Рис. 13.7. Полные двудольные графы K_3,2 и K_3,3

Мы хотели бы знать, какие из полных и полных двудольных графов планарные. Легко показать, что графы K₁, K₂, K₃, K₄, K_m,1 и K_m,2 планарные. Например, на рис. 13.8 мы видим, что K₄ и K_3,2 планарные. Оказывается, что все остальные графы интересующего нас вида непланарные. Воспользуемся формулой Эйлера, чтобы доказать, что K₅ и K_3,3 непланарные.

Рис. 13.8. K₄ и K_3,2 — планарные графы

Чтобы доказать, что K₅ непланарный, мы воспользуемся техникой доказательства от противного. Предположим, что утверждение, которое мы хотим доказать, неверно (т. е. что граф K₅ планарный), и покажем, что это приводит к логическому противоречию. Тогда можно будет заключить, что K₅ непланарный. Г. Х. Харди писал: «Метод доказательства reductio ad absurdum, столь любимый Евклидом, — один из самых лучших инструментов математика. Это гораздо более “хитроумный” гамбит, чем любой шахматный гамбит: шахматист может пожертвовать пешку или даже фигуру, но математик жертвует партию»¹⁰⁴.

Предположим, что K₅ — планарный граф. Тогда мы сможем нарисовать K₅ на плоскости, так что никакие два ребра не будут пересекаться. K₅ имеет 5 вершин и 10 ребер. Формула Эйлера для планарных графов утверждает, что V — E + F = 2, поэтому в нашем планарном чертеже K₅ должно быть 7 граней, включая неограниченную (потому что 2 = F — 10 + 5).

Каждое ребро является общей границей двух граней, поэтому 2E = pF, где p — среднее число сторон по всем граням. K₅ — полный граф, поэтому в нем нет ни петель, ни параллельных ребер. Так как нет петель, то не существует граней, ограниченных только одним ребром, а поскольку нет параллельных ребер, то не существует граней, ограниченных двумя ребрами. Следовательно, среднее число ребер на одну грань должно быть не меньше трех. Это значит, что p ≥ 3 и 2E ≥ 3F. Но из того, что F = 7 и E = 10, следует, что 20 ≥ 21, т. е. мы пришли к противоречию. Поэтому K₅ должен быть непланарным.

Аналогично можно доказать, что полный двудольный граф K_3,3 непланарный (попробуйте сами!). Главное отличие заключается в том, что, поскольку K_3,3 двудольный, путь, который начинается и заканчивается в одной и той же вершине, должен иметь четное число ребер. Поэтому в нем не может быть также граней с тремя сторонами.

В общем случае справедлива следующая теорема.

Оказывается, что в некотором смысле K₅ и K_3,3 — единственные препятствия, мешающие графу быть планарным. Знаменитая теорема Куратовского-Понтрягина утверждает, что граф может быть непланарным, только если он содержит в качестве подграфа K₅ или K_3,3. Например, граф на рис. 13.9 непланарный, потому что содержит копию K₅.

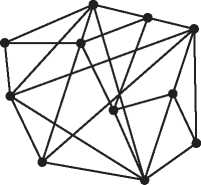
Рис. 13.9. Пример непланарного графа, содержащего K₅

Далее мы приведем еще одно интересное применение формулы Эйлера, называемое теоремой Пика. Ее доказал Георг Александр Пик (1859-ок. 1943) в 1899 году¹⁰⁵. Пик был австрийским математиком, большую часть жизни прожил в Праге. Он погиб в концлагере Терезиенштадт в Чехословакии.

Для формулировки теоремы Пика обратимся к математическому планшету — популярному средству обучения, изобретенному Калебом Гаттеньо (1911–1988), который прекрасно помогает детям изучать основы геометрии. Математический планшет можно изготовить самостоятельно — нужно только вбить в доску гвозди, так чтобы они образовывали квадратную сетку. Учащиеся натягивают на гвозди резинки, формируя разные многоугольники (рис. 13.10). С помощью планшета учитель может обсуждать такие геометрические понятия, как периметр, угол, площадь и теорему Пифагора.

Рис. 13.10. Многоугольник на математическом планшете

Теорема Пика дает простой способ вычисления площадей даже очень сложных невыпуклых многоугольников (мы, однако, требуем, чтобы резинка не пересекала самое себя).

Например, поскольку для многоугольника на рис. 13.10 B = 12 и I = 5, то его площадь равна 5 + 12/2 — 1 = 10.

Оказалось, что один лесник в Орегоне использовал приближение к теореме Пика для оценки площади леса¹⁰⁶. Лесник взял прозрачную пластинку с нанесенной на нее решеткой точек и наложил ее на многоугольную карту своего участка. Для оценки площади он сложил число точек во внутренней области с половиной числа точек на границе (очень близко к теореме Пика!) и умножил на подходящий масштабный коэффициент.

Теорема Пика с легкостью вытекает из формулы Эйлера, при условии что нам известна площадь примитивного треугольника. Треугольник называется примитивным, если внутри него нет гвоздей, а единственные гвозди на границе находятся в вершинах (например, треугольник на рис. 13.11). Иными словами, треугольник примитивный, если B = 3 и I = 0. Удивительно, но площадь любого примитивного треугольника равна 1/2.

Рис. 13.11. Параллелограмм, построенный по примитивному треугольнику на плоскости

К сожалению, доказать этот факт довольно трудно. Вместо полного доказательства мы поясним, почему это должно быть верно. Легко видеть, что плоскость (бесконечный математический планшет) можно замостить квадратами 1*1. Такое замощение обладает тем свойством, что если сдвинуть любую плитку на единицу вверх, вниз, вправо или влево, то она совпадет с другой плиткой. Аналогично возьмем примитивный треугольник и достроим его до параллелограмма, имеющего вдвое большую площадь. Параллелограммами тоже можно замостить плоскость, сдвигая их на единицу вверх, вниз, вправо или влево. Поэтому параллелограмм, как и квадрат, должен иметь площадь 1. А значит, площадь треугольника равна 1/2.

Теперь мы можем доказать теорему Пика. Сначала построим триангуляцию многоугольника — разобьем его на T примитивных треугольников (как показано на рис. 13.12). Если считать неограниченную область гранью, то F = T + 1. Поскольку площадь каждой треугольной грани равна 1/2, то полная площадь многоугольника A = (1/2)T.

Рис. 13.12. Многоугольник разбит на примитивные треугольники

У каждой ограниченной грани три стороны, поэтому в величине 3T каждое ребро учтено дважды, за исключением граничных ребер, которые учитываются один раз. Поскольку число граничных ребер равно числу расположенных на границе вершин, имеем

3T = 2E — B,

или

Количество вершин V = I + B. Применяя формулу Эйлера, получаем

2 = V — Е + F;

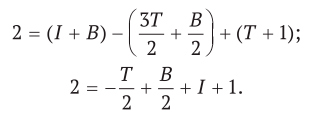
Поэтому число треугольных граней равно

T = 2I + B — 2,

а полная площадь равна

что и требовалось доказать.

И в заключение опишем две игры с карандашом и бумагой. Несмотря на сходство, одна является интеллектуальным вызовом, а другая — насмешкой над игроками, поскольку исход известен еще до того, как сделан первый ход.

По словам Мартина Гарднера (1914–2010), который долгое время вел математическую колонку в журнале «Scientific American», игру «Рассада» придумали за чашкой чая одним февральским утром 1967 года Джон Хортон Конвей (1937–2020) и Майкл Патерсон из Кембриджского университета. Она стала сенсацией. Конвей писал Гарднеру, что «на следующий день после того, как рассада проросла, в нее, казалось, играли все. Во время перерыва на чай или кофе собирались группки людей, склонившихся над фантастически нелепыми позициями рассады»¹⁰⁷.

В начале игры на чистом листе бумаги рисуется несколько точек. Затем игроки по очереди ходят. Ход заключается в том, что игрок соединяет линией (прямой или кривой) две точки либо рисует петлю, начинающуюся и заканчивающуюся в какой-то точке, а потом ставит на этой линии новую точку. Правила очень простые: линии не должны пересекаться, линия не должна проходить через ранее поставленные точки, из каждой точки не должно исходить более трех точек. Победителем считается игрок, сделавший последний возможный ход. На рис. 13.13 показана игра с двумя начальными точками, в которой игрок 2 выигрывает на четвертом ходу.

Рис. 13.13. Игрок 2 выигрывает в «Рассаду»

Чем больше точек нарисовано в начале, тем дольше длится игра, но бесконечно продолжаться она не может. В начале игры с n точками существует 3n мест для присоединения ребра. После проведения каждого нового ребра количество свободных мест уменьшается на единицу (два места использованы, одно добавилось). Поэтому самая длинная игра не может продолжаться более 3п — 1 ходов.

Оказывается, что при небольших n преимущество есть у первого или второго игрока, в зависимости от числа точек. Если в начале игры всего две точки, то второй игрок всегда может делать ходы, гарантированно приводящие к выигрышу. Это верно также для n = 1, 6, 7, 8. С другой стороны, первый игрок имеет преимущество при n = 3, 4, 5, 9, 10, 11. Большая часть этих случаев (n > 6) была проверена на компьютере¹⁰⁸. Для следующих значений n неизвестно, имеет ли какой-то игрок преимущество. Хотя теоретически эта игра несправедлива, конкретная выигрышная стратегия известна только для самых малых n. В любом случае на практике для выигрыша нужно приложить интеллектуальные усилия.

Впоследствии Конвей придумал вариант «Рассады», который назвал «Брюссельская капуста». Вначале рисуется не n точек, а n плюсиков. Игроки по очереди соединяют свободные концы плюсиков линией и ставят на ней новый плюсик (с двумя свободными концами) (см. рис. 13.14). В отличие от «Рассады», правила «Брюссельской капусты» позволяют сходиться в одной вершине четырем ребрам. Как и раньше, победителем считается игрок, сделавший последний ход. Как выяснилось, забавное название «Брюссельская капуста» было намеком на то, что и сама игра шуточная.

Мы видели, что «Рассада» обязательно заканчивается, но для «Брюссельской капусты» это не так очевидно. Каждый ход убирает два свободных конца, но и добавляет два новых, поэтому кажется, что игра может продолжаться бесконечно. Однако конец любой партии в «Брюссельскую капусту» предопределен, и в этом и состоит шутка. Какими бы гениальными или тупыми ни были игроки, игра всегда заканчивается после 5n — 2 ходов — не больше, не меньше. Иными словами, если вначале было нечетное число плюсиков, то гарантированно выиграет первый игрок, иначе лавры победителя достанутся второму игроку.

Рис. 13.14. Игрок 2 выигрывает в «Брюссельскую капусту»

Если игнорировать свободные концы плюсиков, то на каждом ходу игровое поле представляет собой планарный граф (быть может, состоящий из нескольких компонент связности). Если считать плюсиками вершинами, то каждый ход добавляет два ребра и одну вершину. Если новая линия не соединяет две компоненты связности, то каждый ход добавляет также одну грань.

Мы утверждаем, что игра закончится, когда граф станет связным и будет иметь ровно 4n граней (внешняя область тоже считается гранью). В начале игры имеется n плюсиков с 4n свободными концами. Поскольку каждый ход убирает два свободных конца и добавляет два новых, всегда имеется 4n свободных концов. Для любой грани должен существовать по крайней мере один свободный конец, указывающий внутрь нее, а именно тот, что принадлежит последней нарисованной линии, ограничивающей ее. Таким образом, граф имеет не более 4n граней. С другой стороны, если граней меньше 4n, то какая-то грань должна содержать два свободных конца, поэтому игра еще не закончена.

Предположим, что игра заканчивается после m ходов, и в результате получается связный граф с V вершинами, E ребрами и F = 4n гранями. (В финальной конфигурации на рис. 13.15 V = 10, E = 16, F = 8.) Как уже было сказано, на каждом из m ходов добавляется два новых ребра и одна новая вершина. Поскольку в начале игры ребер не было, а вершин было n, то в конце мы будем иметь E = 2m ребер и V = n + m вершин. По формуле Эйлера:

2 = V — E + F = (n + m) — 2m + 4n.

Отсюда m = 5n — 2.

Рис. 13.15. Финальный граф игры в брюссельскую капусту на рис. 13.14

Так что если хотите подшутить над своими ничего не подозревающими друзьями, предложите им сыграть в «Брюссельскую капусту». Разрешите им выбрать либо очередь хода, либо начальное количество плюсиков. В любом случае вы сможете гарантировать себе выигрыш.

Приложения к главе

103. Hankel (1884).

104. Hardy (1992), 94.

105. Pick (1899).

106. DeTemple (1989).

107. Gardner (1975a), 8.

108. Applegate, Jacobson, and Sleator (1991).