Жемчужина Эйлера

Глава 19 Как причесать ежа

Многие ученые используют математику как средство для предсказания поведения. Ученый может располагать уравнением или системой уравнений, описывающих взаимодействие величин в модели. И пользуется математикой, чтобы вывести из этих уравнений какие-то заключения.

Часто математические модели выражаются с помощью дифференциальных уравнений. Они описывают скорости изменения различных величин со временем. Например, эколог может составить систему дифференциальных уравнений для моделирования популяционной динамики кроликов и лис в заповеднике, обусловленной отношениями между хищником и добычей. Когда кроликов много, лисы наслаждаются изобилием пищи. За счет этого их число растет, а число кроликов падает. В конечном итоге запас пищи у лис иссякает, поэтому их популяция уменьшается. И теперь наступает черед процветать кроликам. Такое циклическое поведение показано на рис. 19.1.

Рис. 19.1. Модель хищник-добыча

Дифференциальные уравнения записываются в виде алгебраического соотношения между переменными и их производными. Говоря о решении дифференциального уравнения, мы имеем в виду, что при заданных начальных условиях можно предсказать будущее поведение системы. Иными словами, если мы знаем, сколько кроликов и лис имеется сегодня, то сможем предсказать, сколько их будет через год. Кривая на рис. 19.1 — график решения. Стрелками показано положительное направление времени. Кривая построена в фазовом пространстве — топологическом объекте, представляющем все возможные значения переменных. В данном случае фазовым пространством является первый квадрант плоскости (поскольку число кроликов и лис должно быть неотрицательно). В более экзотических примерах фазовое пространство может иметь топологически более сложную форму.

Иногда ученому недостаточно найти конкретное решение дифференциального уравнения. Часто более важны качественные выводы. Обладает ли система равновесным состоянием — популяциями, в которых для обоих видов частота смертей равна частоте рождений? Существуют ли начальные условия, при которых один или оба вида обречены на вымирание? А условия, ведущие к взрывному росту популяции? Будет ли поведение популяций носить циклический характер, или оно хаотично? Даже если мы в состоянии найти аналитическое решение дифференциального уравнения, ответить на такие важные «глобальные» вопросы не всегда легко.

Чтобы лучше понять, как устроены решения системы дифференциальных уравнений, необходим более наглядный, геометрический способ их представления. Есть два распространенных метода: порождение потока или векторного поля в фазовом пространстве. Поток, называемый также непрерывной динамической системой, ассоциирует с каждой точкой фазового пространства траекторию движения точки. Эта траектория попросту представляет собой кривую решения дифференциального уравнения. Несколько таких траекторий для модели хищник-добыча показаны на рис. 19.2. Видно, что для любой неравновесной пары начальных популяций их численности циклически увеличиваются и уменьшаются.

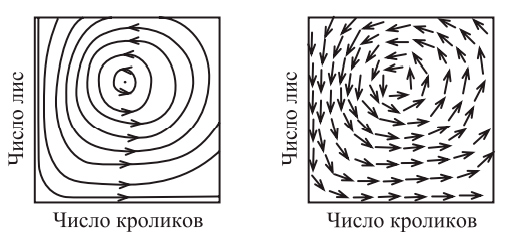
Рис. 19.2. Поток и векторное поле, ассоциированные с моделью хищник-добыча

Вместо того чтобы выражать дифференциальное уравнение алгебраически или в виде потока, мы можем описать его в терминах векторного поля. В отличие от скалярных величин, таких как температура, время, яркость или масса, которые можно описать одним значением, векторные величины имеют величину и направление. В физике вектором описывается скорость: вектор указывает направление движения, а его абсолютная величина (модуль) представляет быстроту перемещения объекта. Можно было бы привести и другие примеры, но пример скорости, наверное, самый интуитивно понятный. На самом деле если интерпретировать поток как движение частиц, то векторное поле состоит из векторов скоростей этих частиц в фазовом пространстве.

На рис. 19.2 мы видим единственную точку равновесия, в которой число лис и кроликов остается неизменным. Абсолютная величина вектора в точке равновесия равна нулю, поэтому говорят, что в этой точке векторное поле имеет ноль. А для потока это неподвижная точка, или точка покоя. Нули векторного поля часто играют огромную роль, потому что представляют точки равновесия системы.

Остаток этой главы мы посвятим исследованию векторных полей на поверхностях, а не порождающим их дифференциальным уравнениям. Наша основная цель — понять связь между нулями векторного поля и топологией поверхности.

Один из самых простых способов получить векторное поле на поверхности — поместить поверхность в трехмерное пространство и считать, что векторы «указывают в направлении подножья горы», и чем круче спуск, тем длиннее вектор. Это называется градиентным векторным полем. На рис. 19.3 показано градиентное векторное поле на сфере и торе. Чтобы представить себе поток, ассоциированный с векторным полем, вообразим, что поверхность покрыта патокой. Тогда траектории потока — это просто пути, по которым вязкий сироп сползает вниз по поверхности.

Рис. 19.3. Градиентные векторные поля на сфере и на торе

На рис. 19.3 видно, что градиентные векторные поля на сфере и на торе имеют нули — на сфере их два (один на северном полюсе, другой на южном), а на торе четыре (верхняя и нижняя точки тора и верхняя и нижняя точки дырки). Верно ли, что любое векторное поле на сфере имеет ноль? А на торе? Если мы сможем утвердительно ответить на этот вопрос для некоторой поверхности S, то получим очень сильный результат. Он означает, что если фазовым пространством системы является S, то у системы обязательно существует точка равновесия.

Частичный ответ на эти вопросы дает красивая теорема Пуанкаре-Хопфа. Она устанавливает неожиданную связь между нулями векторного поля и эйлеровой характеристикой. Чтобы понять, в чем ее суть, мы должны внимательнее познакомиться с нулями векторных полей.

Не все нули одинаковы. На рис. 19.4 мы видим пять различных нулей и соответствующие им неподвижные точки потока. Поведение в окрестности этих нулей сильно различается. Источник отталкивает все близлежащие точки, сток притягивает их, седло делает то и другое, точки вокруг центра обтекают неподвижную точку, а точки вокруг диполя утекают, а затем притекают обратно (похоже на линии магнитного поля вокруг стержневого магнита).

Рис. 19.4. Векторные поля в окрестности нуля и соответствующие им потоки

Источники, стоки и седла часто встречаются как нули градиентного потока. На рис. 19.5 мы видим источник в верхней точке перевернутой чаши, сток в нижней точке чаши, а седло в середине седлообразной поверхности. Заметим, что на рис. 19.3 градиентный поток на сфере имеет один источник и один сток, а градиентный поток на торе — один источник, один сток и два седла.

Интуиция подсказывает, что стоки, седла и источники чем-то различаются и должно существовать правило, описывающее количество нулей каждого типа. Из примера градиентного потока мы видим, что на сфере может находиться векторное поле с двумя нулями, но трудно представить себе векторное поле на сфере с одним стоком и одним седлом. Ключевая идея, позволяющая различать нули, — индекс.

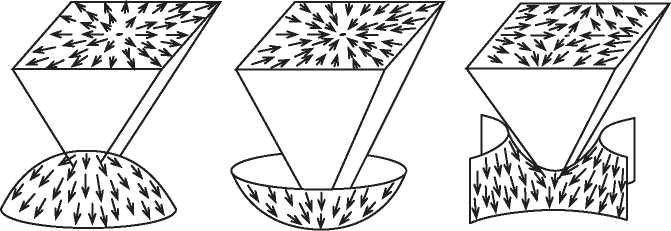
Рис. 19.5. Источник, сток и седло в градиентном векторном поле

Индекс нуля вычисляется следующим образом. Нарисуем вокруг нуля небольшую окружность, удовлетворяющую всего двум условиям: (1) она должна содержать только один ноль и (2) она должна быть краем диска (например, на торе такая окружность не может охватывать трубку или центральную дырку). Теперь поместим в каждую точку на окружности воображаемый циферблат. Стрелка циферблата должна указывать в том же направлении, что векторное поле. (Если бы векторное поле описывало магнитное поле, то в качестве циферблата можно было бы использовать компас.) Если мы будем перемещать циферблат вдоль окружности, то стрелка будет поворачиваться. Переместим циферблат на один оборот против часовой стрелки. Всякий раз, как стрелка один раз повернется против часовой стрелки, будем прибавлять к индексу единицу, а всякий раз, как она повернется по часовой стрелке, будем вычитать единицу. Индекс часто называют числом вращения векторного поля вокруг нуля.

Рассмотрим сток на рис. 19.6. Мы видим циферблат в восьми положениях на окружности. Когда циферблат совершает один оборот вокруг окружности против часовой стрелки, его стрелка один раз поворачивается против часовой стрелки. Поэтому индекс стока равен 1. Для седла стрелка совершает один оборот по часовой стрелке, когда циферблат один раз обходит нуль против часовой стрелки. Поэтому индекс седла равен –1. Аналогично вычисляются индексы остальных нулей на рис. 19.4. Индекс источника и центра равен 1, а индекс диполя равен 2.

Теперь опишем второй способ вычисления индекса векторного поля. Он пригодится нам в дальнейшем. Поместим ноль во внутреннюю область многоугольной грани (она может иметь и закругленные ребра). Многоугольник должен удовлетворять нескольким условиям, а в остальном может быть любым. Как и раньше, многоугольник следует выбирать так, чтобы в нем не было других нулей и чтобы он ограничивал диск. Кроме того, потребуем, чтобы любой вектор, начинающийся на ребре, указывал внутрь или наружу. Нам не нужны векторы, указывающие вдоль ребра. (Такой многоугольник всегда существует, хотя это и не очевидно.) На рис. 19.7 мы видим седло внутри квадрата и сток внутри шестиугольника, расположенные таким образом, что все векторы указывают внутрь или наружу.

Рис. 19.6. Индекс стока равен 1, а индекс седла равен –1

Рис. 19.7. Индекс седла равен 2(–1) + 1 = –1, а индекс стока — 6(–1) + 7(–1) = 1

Теперь выделим ребра и вершины, в которых векторное поле указывает внутрь. На каждом таком ребре поставим –1, а в каждой вершине 1. Наконец, поставим 1 в середину многоугольника. Оказывается, что сумма всех этих чисел равна индексу нуля. Мы видим, что это верно для седла и стока на рис. 19.7.

Вот теперь, наконец, мы можем сформулировать теорему Пуанкаре-Хопфа. Она дает топологический способ определить, есть ли ноль у векторного поля (или, что эквивалентно, есть ли неподвижная точка у потока). Кроме того, она проясняет вопрос об относительном числе нулей каждого типа на конкретной поверхности.

Прежде чем доказывать эту теорему, приведем несколько примеров. На рис. 19.8 показано три разных векторных поля на сфере. Первое, градиентное векторное поле, имеет сток и источник (оба с индексом 1), второе — два центра (оба с индексом 1), а третье — один диполь (с индексом 2). Во всех трех случаях сумма индексов равна 2 — эйлеровой характеристике сферы.

Рис. 19.8. Три векторных поля на сфере

Выше мы видели, что градиентное векторное поле на торе (рис. 19.3) имеет четыре нуля — один источник, два седла и один сток. Сумма их индексов равна 1 + 2(–1) + 1 = 0, т. е. эйлеровой характеристике тора.

В качестве дополнительного бонуса градиентные векторные поля позволяют вычислять эйлерову характеристику поверхностей, не рисуя вершин, ребер и граней. На рис. 19.9 мы видим сферу, согнутую в виде U-образного тела. Градиентное векторное поле имеет два источника, одно седло и один сток, поэтому сумма индексов равна 2(1) + 1(–1) + 1(1) = 2. Двойной тор имеет один источник, четыре седла и один сток, поэтому χ(двойной тор) = 1 + 4(–1) + 1 = –2. На бутылке Клейна один источник, два седла и один сток, поэтому χ(бутылка Клейна) = 1 + 2(–1) + 1 = 0. Подведем итог:

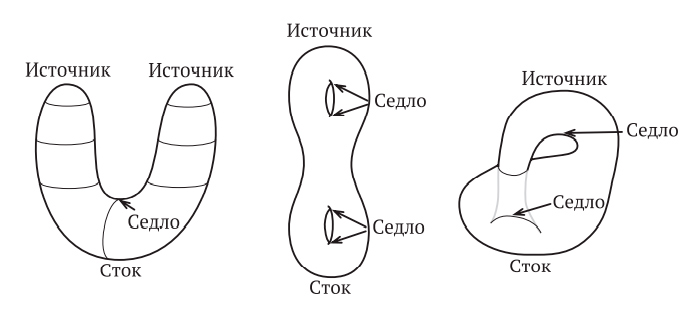
Рис. 19.9. Эйлеровы характеристики сферы, двойного тора и бутылки Клейна соответственно равны 2, –2 и 0

Теорема Пуанкаре-Хопфа утверждает, что если число нулей векторного поля на поверхности конечно, то сумма их индексов равна эйлеровой характеристике. Отсюда следует, что если у векторного поля нет нулей, то эйлерова характеристика поверхности должна быть равна нулю. Поэтому любое векторное поле на поверхности с ненулевой эйлеровой характеристикой обязано иметь по крайней мере один ноль! Эйлерова характеристика сферы равна 2, следовательно, любое векторное поле на сфере должно иметь ноль. Эта знаменитая теорема, которую первым доказал Л. Э. Дж. Брауэр (1881–1966), известный друзьям как «Бертус», в 1911 году¹⁷¹, имеет хорошо запоминающееся название — теорема о причесывании ежа. Так она называется, потому что если рассматривать свернувшегося в клубок ежа (или теннисный мяч) как сферу с векторным полем, то невозможно причесать его так, чтобы ни одна иголка не торчала.

Из этой теоремы следует утверждение, упомянутое во введении: в любой момент времени на Земле существует точка, в которой не дует ветер. Если рассматривать Землю как сферу, то направления ветров на поверхности образуют векторное поле. По теореме о причесывании ежа, существует точка, где это поле обращается в ноль. В примере на рис. 19.10 точка безветрия находится в центре циклона близ берегов Южной Америки. (На самом деле, поскольку индекс этого нуля равен 1, на другой стороне Земли должна быть еще хотя бы одна точка, в которой нет ветра!)

Рис. 19.10. Векторы направления ветра на поверхности Земли

Поскольку эйлерова характеристика тора равна нулю, теорема Пуанкаре-Хопфа не гарантирует, что любое векторное поле на нем имеет ноль. И действительно, на рис. 19.11 приведен пример не обращающегося в ноль векторного поля на торе.

Рис. 19.11. Векторное поле без нулей на торе

Теорема о причесывании ежа — пример «теоремы существования». Таких в математике много. Они одновременно очень мощные и мучительно неточные. С одной стороны, при очень простом наборе предположений (векторное поле на сфере) мы можем уверенно говорить о существовании некоторого объекта (нулевого вектора). С другой стороны, часто бывает так, что ни формулировка, ни способ доказательства теоремы существования никак не помогают найти этот объект. Мы знаем, что где-то на другой стороне земного шара (см. рис. 19.10) есть точка безветрия, но она может быть где угодно, и, более того, таких точек может быть одна или много. Это все равно, что искать засунутого куда-то плюшевого мишку, когда ребенку пора спать, — мы точно знаем, что он где-то дома, но где — под кроватью, в шкафу или в микроволновке? Хотя для нахождения таких объектов нужны дополнительные методы, часто одного лишь знания о его существовании достаточно для конкретной цели.

Теорема Пуанкаре-Хопфа названа в честь двух математиков, внесших наибольший вклад в ее доказательство, хотя были и другие.

Анри Пуанкаре родился во Франции, в городе Нанси в 1854 году в респектабельной состоятельной семье (его двоюродный брат Раймон Пуанкаре позже станет президентом Французской республики).

Рис. 19.12. Анри Пуанкаре

Математический талант Пуанкаре проявился очень рано, а один из учителей называл его «монстром математики»¹⁷². Первые математические открытия он сделал, когда ему еще не было и тридцати лет, а в Академию наук был избран в возрасте тридцати трех лет. Он был типичным математическим гением: неуклюжий, близорукий, рассеянный. Но обладал выдающимся интеллектом и способностью удерживать в мозгу и мысленно жонглировать многочисленными абстрактными понятиями.

Пуанкаре всеми признан как виднейший математик своего времени. Он был настоящим универсалом. Подобно Эйлеру и Гауссу, Пуанкаре был специалистом почти во всех областях математики, чистой и прикладной. Он жадно проглатывал литературу и был в курсе всех последних результатов. Как и Эйлер (но не Гаусс), Пуанкаре много печатался. Из-под его пера вышло почти пятьсот статей, а также много книг и материалов к лекциям. Он внес важный и не теряющий значения с годами вклад в такие разные области, как теория функций, алгебраическая геометрия, теория чисел, дифференциальные уравнения — обыкновенные и в частных производных, небесная механика, динамические системы и, конечно, топология. Он также опубликовал много статей по теоретической физике. Для Пуанкаре было характерно неистощимое любопытство, которое вело его от одного предмета к другому. Бывало, что он набрасывался на новую область математики, оставлял в ней неизгладимый след, а затем переходил к следующей. Один современник назвал его «завоевателем, но не колонистом».

Удивительно, что он не только умел делать первоклассную математику, но и писать на уровне, доступном неспециалистам. Он автор многочисленных ярких и увлекательных публикаций о науке и математике для широкой аудитории. Его тексты переведены на многие языки, их читают во всем мире.

Интересы Пуанкаре охватывали всю математику, но на протяжении всей карьеры он снова и снова возвращался к изучению дифференциальных уравнений. Его успехи в этой области поражают воображение. По словам математика Жана Дьедонне (1906–1992), «самым выдающимся плодом творчества Пуанкаре стала… качественная теория дифференциальных уравнений. Это один из немногих примеров математической теории, которая внезапно возникла из ниоткуда и почти сразу достигла совершенства в руках своего создателя»¹⁷³. Показательным примером стало его открытие формулы индекса.

Свой первый вклад Пуанкаре сделал в 1881 году. В этой работе он взял дифференциальное уравнение и построил векторное поле на сфере. Он определил индекс нуля и доказал, что сумма индексов всех нулей равна 2⁵¹⁷⁴. Конечно, это не простое совпадение, поскольку 2 совпадает с эйлеровой характеристикой сферы. Пуанкаре явно сформулировал это наблюдение в 1885 году, доказав, что сумма индексов нулей векторного поля на поверхности равна ее эйлеровой характеристике¹⁷⁵. В следующем году он определил индекс нуля векторного поля в n-мерном пространстве и представил набросок идеи n-мерной теоремы об индексе. Трудность развития этой программы заключалась в том, что топологического аппарата еще не существовало (его, как мы увидим в главе 23, Пуанкаре создал позднее).

В 1911 году Брауэр обобщил теорему Пуанкаре об индексе на n-мерную сферу Sⁿ. Мы знакомы с S¹, единичной окружностью на плоскости (x² + у² = 1), и S², единичной сферой в трехмерном пространстве (x² + y² + z² = 1). Вообще, Sⁿ — это множество точек, удаленных на расстояние 1 от начала координат в (n + 1) — мерном пространстве (x₁² + x₂² +… + x²_n+1 = 1). Брауэр доказал, что для любого векторного поля на Sⁿ сумма индексов нулей равна 0, если n нечетно, и 2, если n четно¹⁷⁶. В главах 22 и 23 мы обсудим эйлерову характеристику в многомерных пространствах. И узнаем, что χ(Sⁿ) = 0, когда n нечетно, и χ(Sⁿ) = 2, когда n четно.

Следующим из основных соавторов был Хайнц Хопф (1894–1971). Хопф родился в немецком городе Бреслау (ныне Вроцлав в Польше). Его труды по топологии оказали значительное влияние на математику XX века. Один ученик Хопфа писал: «Хопф с безошибочным инстинктом выбирал глубокие проблемы и давал им возможность созреть. А затем представлял целостное решение, демонстрирующее новые мысли и методы»¹⁷⁷.

Рис. 19.13. Хайнц Хопф

В своих мемуарах Хопф отмечает, что поворотным моментом в его математической карьере стал двухнедельный период в 1917 году — отпуск с военной службы во время Первой мировой войны. Он сидел на занятиях в университете Бреслау во время изложения топологической теоремы Брауэра. После службы на Западном фронте, где он был дважды ранен и получил Железный крест, он возобновил изучение математики в университете Бреслау. Его математическая карьера заводила его в несколько немецких университетов, Принстонский университет и, наконец, в Швейцарскую высшую техническую школу (ETH) в Цюрихе.

Через два года после его приезда в Швейцарию к власти в Германии пришла нацистская партия. Хотя он воспитывался в протестантской вере, его отец был евреем. Соломон Лефшец и другие принстонские ученые убеждали Хопфа вернуться, но они с женой отказались покидать Швейцарию, а старались помогать беженцам из Германии. В конце концов, немецкое правительство пригрозило лишить его гражданства в случае невозвращения. С неохотой он отказался от немецкого гражданства и принял швейцарское. После войны Хопф остался в Швейцарии и усердно работал над восстановлением математики в Германии.

Из многочисленных важных вкладов Хопфа в топологию одним из первых стала топология векторных полей. Начиная с 1925 года он опубликовал серию статей, обобщающих теорему Пуанкаре об индексе¹⁷⁸. Мы сформулировали теорему Пуанкаре-Хопфа для поверхностей, но Хопф доказал, что она применима и к многомерным обобщениям поверхностей — многообразиям (мы еще поговорим о многообразиях в главе 22).

Хотя теорема Пуанкаре-Хопфа обычно формулируется для замкнутых поверхностей, математики открыли различные ее обобщения. Существует очень общий вариант для поверхностей с краем¹⁷⁹, но мы сформулируем следующую более простую версию.

Теорема о причесывании ежа неприменима к нашим головам, потому что волосистая часть головы человека топологически не является сферой — это диск. И действительно, в «зачесанных назад» прическах и «конских хвостах» волосы не торчат. Но у человека, подстриженного «ежиком», волосы часто растут в направлении от центра головы — вниз на затылке, к ушам по бокам и в сторону лица спереди. Поскольку это «волосяное» векторное поле направлено наружу вдоль края, то сумма индексов нулей должна быть равна χ(диск) = 1. Поэтому в каком-то месте головы должен быть вихор. У маленькой дочки автора (на голове у которой пока еще растет пушок) есть зачатки трех вихров, двух спиралей, закрученных наружу (все с индексом 1) и седло между ними (с индексом 0).

Теперь мы наметим доказательство теоремы Пуанкаре-Хопфа для поверхностей без края (его нетрудно модифицировать для поверхностей с краем). Доказательство основано на идее Уильяма Тёрстона (1946–2012)¹⁸⁰.

Начнем с тщательно выбранного разбиения поверхности. Сначала поместим каждый ноль векторного поля внутрь многоугольной грани, не содержащей других нулей. Эти грани могут иметь произвольную форму, с любым числом сторон, при условии что ни один вектор, начинающийся на ребре, не направлен параллельно ребру. То есть всякий вектор на границе должен указывать внутрь или наружу.

Сейчас мы имеем грани, охватывающие все нули векторного поля. Завершим разбиение, триангулировав оставшуюся часть поверхности. Это можно сделать как угодно, но, как и раньше, мы требуем, чтобы все векторы, начинающиеся на границах треугольников, были направлены внутрь или наружу, но не вдоль ребра (см. рис. 19.14).

Теперь поместим 1 в каждую вершину, –1 на каждое ребро и 1 — в центр каждой грани. Просуммировав эти числа по всей поверхности, мы получим V — E + F, или χ(S). Точнее, поскольку каждое ребро является общей границей двух граней, а векторное поле направлено внутрь одной из этих граней, будем располагать относящуюся к ребру –1 внутри той грани, в направлении которой указывает вектор. Аналогично каждая вершина расположена в точке схождения нескольких граней, но есть одна, внутрь которой указывает вектор. Поставим 1 именно в этой грани (см. рис. 19.14).

Рис. 19.14. Разбиение поверхности на грани, содержащие не более одного нуля, и соответствующая пометка вершин, ребер и граней

Сначала рассмотрим треугольные грани, не содержащие нулей векторного поля. Как показано на рис. 19.15, возможно всего два случая. Первый — когда векторы направлены внутрь на одном ребре и ни в одной вершине. Второй — когда векторы направлены внутрь на двух ребрах и на вершине между ними. В обоих случаях сумма 1 и –1 равна нулю. Поэтому эти треугольные грани не дают никакого вклада в эйлерову характеристику.

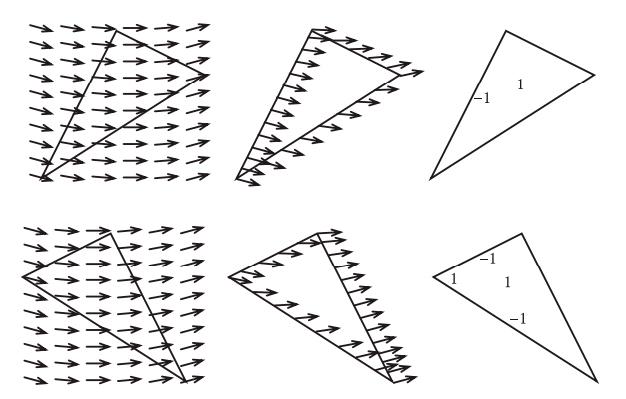
Рис. 19.15. Треугольники, не содержащие нулей, не дают никакого вклада в эйлерову характеристику

С другой стороны, вспомним, что для граней, содержащих нули, эту технику можно использовать для вычисления индекса. Таким образом, каждая грань, содержащая ноль, вносит в сумму вклад, равный индексу этого нуля. По теореме Пуанкаре-Хопфа, сумма всех 1 и –1 равна, с одной стороны, эйлеровой характеристике, а с другой — сумме индексов нулей.

Как уже было сказано, теорема Пуанкаре-Хопфа говорит о векторных полях, но поскольку векторные поля можно использовать для построения потоков, то ее можно интерпретировать так же, как теорему о неподвижной точке непрерывной динамической системы. В заключение этой главы мы упомянем еще одну знаменитую теорему о неподвижной точке.

Поток на поверхности — это математический способ описать непрерывное движение частиц. Теперь мы рассмотрим родственную, но совершенно иную ситуацию. Предположим, что вместо того чтобы течь, каждая точка на поверхности S перепрыгивает в новое положение. Математически это движение можно описать с помощью непрерывной функции f с областью определения S и областью значений S (говоря «непрерывная», мы просто имеем в виду, что близкие точки переходят в близкие). Первоначально точка имеет координату x, а затем перемещается в новую точку с координатой f (x). Как и в случае потоков, нас особенно интересуют точки, которые остаются на месте. Точка y на поверхности S называется неподвижной точкой f, если f (y) = y (см. рис. 19.16).

Рис. 19.16. Точка y является неподвижной точкой f, а x — нет

Пожалуй, самой знаменитой из всех теорем о неподвижной точке является теорема Брауэра. Она применима к непрерывной функции из n-мерного шара в него же. N-мерным шаром Вⁿ называется множество всех точек n-мерного пространства, удаленных от начала координат на расстояние, не большее единицы. Иначе говоря, это множество точек, удовлетворяющих неравенству x²₁ + x²₂ +… + х²_n+1 ≤ 1, или попросту — множество точек внутри и на поверхности (n — 1) — мерной сферы S^n-1. Свой результат Брауэр доказал для B³ 1909 году¹⁸¹, а для Вⁿ (n > 3) в 1912 году¹⁸².

Рис. 19.17. Векторное поле для функции из В² в себя

Интерпретировать эту замечательную теорему можно, например, следующим образом. Рассмотрим случай n = 2. B² — это диск на плоскости, т. е. область, ограниченная единичной окружностью S¹. Представим, что это столовая тарелка. Накроем ее листом бумаги, по размеру не меньшим тарелки, а затем отрежем свисающие части. Теперь возьмем бумагу, сомнем ее в комок (но не рвать!) и снова положим на тарелку. Теорема Брауэра утверждает, что на бумаге найдется точка, расположенная в точности против того места на тарелке, где была раньше. Такое же рассуждение показывает, что если проектировщик одноэтажного гипермаркета поместит его карту в любом месте на полу, то он сможет поставить на карте крестик, означающий «вы находитесь здесь».

Доказательство этой теоремы легко следует из теоремы Пуанкаре-Хопфа (ее варианта для поверхностей с краем). Мы будем рассматривать случай n = 2, но для больших n доказательство точно такое же. Начнем с функции f из B² в себя. Определим на B² векторное поле следующим образом: каждой точке x, принадлежащей B², сопоставим вектор, начинающийся в x и заканчивающийся в f(x) (см. рис. 19.17). B² — поверхность с краем, и все векторы, начинающиеся в точках края, направлены внутрь, поэтому условия теоремы Пуанкаре-Хопфа выполнены. Поскольку 'χ(B²) = 1 ≠ 0, векторное поле должно иметь хотя бы один ноль. Но нулевой вектор соответствует точке y, для которой f(y) = y. Иными словами, f должна иметь хотя бы одну неподвижную точку.

На самом деле теорема Брауэра применима к любому телу, гомеоморфному Bⁿ. Кофе в чашке гомеоморфно B³. Как следует размешайте кофе в чашке (но не проливайте ни капли!) и подождите, пока оно снова успокоится. Тогда, по теореме Брауэра о неподвижной точке, найдется молекула кофе, находящаяся точно в том же месте, что и в самом начале.

В этой главе мы видели, что топология объекта, определяемая одной лишь характеристикой Эйлера, может влечь за собой глобальное поведение, которое, казалось бы, не имеет никакого отношения к глобальной топологии, — существование неподвижных точек у потоков и функций. В следующих двух главах мы увидим, что топология фигуры может определять также некоторые ее глобальные геометрические свойства.

Приложения к главе

170. Frost (2002), 308.

171. Brouwer (1912).

172. цитируется по Dieudonne (1975).

173. Dieudonne (1975).

174. Poincare (1881).

175. Poincare (1885).

176. Brouwer (1912).

177. Beno Eckmann, quoted in Frei and Stammbach (1999).

178. Hopf (1925); Hopf (1926a); Hopf (1926b).

179. Morse (1929).

180. Thurston (1997).

181. Brouwer (1909).

182. Brouwer (1912).