Жемчужина Эйлера

Глава 8 Платоновы тела, мячи для гольфа, фуллерены и геодезические купола

Все это замечательно, только кому это нужно?» — спросит скептически настроенный студент, источая сарказм. Красота — чудесная вещь, но некоторые считают, что важность теоремы следует измерять ее полезностью. Для чего может пригодиться формула Эйлера?

Этот вопрос можно задать применительно к любой математической теореме. Формула Эйлера — больше, чем просто элегантная теорема. В последующих главах мы представим многочисленные применения формулы Эйлера. Для большей их части придется провести кое-какую подготовку, чтобы понять, в чем состоит применение. Но чтобы разжечь у читателя аппетит, мы сделаем паузу и опишем два простых применения. Сначала мы с помощью формулы Эйлера докажем, что не существует правильных многогранников, кроме платоновых тел, а затем воспользуемся ей, чтобы вывести структурную теорему для мячей для гольфа, больших молекул и геодезических куполов.

В главе 5 мы показали, как Евклид доказывал, что существует ровно пять платоновых тел. Хотя доказательство кажется коротким, оно опирается на геометрические теоремы, доказанные в предыдущих двенадцати книгах «Начал». В этой главе мы приведем другое доказательство этого факта, основанное на формуле Эйлера и простых арифметических выкладках.

Пусть имеется правильное тело. Мы покажем, что это должно быть одно из пяти известных платоновых тел: тетраэдр, куб, октаэдр, икосаэдр или додекаэдр. Предположим, что многогранник имеет V вершин, E ребер и F граней. Из формулы Эйлера мы знаем, что

V — E + F = 2.

Поскольку многогранник правильный, каждая его грань является правильным многоугольником, и все они имеют одно и то же число ребер. Очевидно, что это число, которое мы обозначим n, должно быть не меньше трех. По определению, в каждой вершине сходится одно и то же число ребер. Это число m также должно быть не меньше трех (разумеется, m также равно числу граней, сходящихся в каждой вершине).

Каждая грань привносит n ребер, но поскольку каждое ребро является общим для двух граней, в величине Fn каждое ребро учтено дважды. Иначе говоря,

E = ½(Fn).

Аналогично каждая грань привносит n вершин, но в каждой вершине сходится m граней, поэтому в величине Fn каждая вершина учтена m раз. Таким образом,

V = Fn/m.

Теперь подставим эти величины в формулу Эйлера и решим уравнение относительно F.

Мы знаем, что 4m и F положительны. Поэтому чтобы последнее равенство могло иметь место, должно быть

2n — mn + 2m > 0.

Легко проверить, что этому неравенству удовлетворяет только пять пар целых чисел, при условии что n ≥ 3 и m ≥ 3. Вот они: (3, 3), (3, 4), (3, 5), (4, 3), (5, 3). Из формул для V, E и F выше находим, что эти пары соответствуют пяти платоновым телам (табл. 8.1).

Задумаемся об удивительности этого доказательства. Доказательство Евклида было локальным и геометрическим. Он пользовался величинами углов правильных многоугольников, чтобы определить возможные конфигурации в вершинах. И эту локальную информацию он использовал, чтобы сделать вывод о глобальной природе многогранника.

Таблица 8.1. Единственные пять пар целых чисел (n, m), удовлетворяющие требованиям для правильного многогранника

Новое же доказательство глобально и практически не прибегает к геометрии. Это теорема о правильных телах, но нигде в доказательстве не используется тот факт, что грани — правильные многоугольники! Мы даже не предполагали, что грани конгруэнтны. Формула Эйлера по природе своей комбинаторная — в ней подсчитываются вершины, ребра и грани. Нет никакой возможности включить в формулу Эйлера длины сторон и величины углов, и тем не менее мы сумели воспользоваться ей для нахождения всех платоновых тел.

Поскольку мы не использовали все условия теоремы, то, стало быть, доказали нечто совсем иное. Мы лишь предполагали, что все грани имеют одинаковое число сторон и что в каждой вершине сходится одинаковое число граней. С этой точки зрения, все фигуры на рис. 8.1 одинаковы — все они похожи на куб.

Рис. 8.1. Кубоподобные тела

По существу, мы доказали, что существует всего пять конфигураций многогранников, обладающих тем свойством, что все грани имеют одно и то же число сторон и в каждой вершине сходится одинаковое число граней. Любой такой многогранник должен быть «похож» на тетраэдр, октаэдр, икосаэдр, куб или додекаэдр — как многогранники на рис. 8.1 напоминают куб. В частности, число вершин, ребер и граней должно быть таким же, как у одного из платоновых тел.

Стремясь создать мяч для гольфа с улучшенными аэродинамическими свойствами, одна компания изобрела многогранные мячи. Поверхность мяча не покрыта сферическими лунками, а состоит из 232 вдавленных многоугольных граней (рис. 8.2). Поначалу поверхность кажется морем шестиугольных граней. Но будьте уверены, это не шестое платоново тело. При ближайшем рассмотрении мы обнаружим, что 12 граней — пятиугольники.

Рис. 8.2. Мяч для гольфа состоит из 220 шестиугольников и 12 пятиугольников

Во введении мы узнали о семействе шарообразных молекул углерода, называемых фуллеренами. На рис. 8.3 показан бакминстерфуллерен C₆₀, имеющий форму футбольного мяча. Атомы углерода образуют 12 пятиугольных и 20 шестиугольных колец. Ученые умеют создавать фуллерены с другим числом атомов углерода. Например, C₅₄₀ — массивный фуллерен с 540 атомами. Соответствующий этой молекуле многогранник состоит из 12 пятиугольников и 260 шестиугольников. Вообще, любой фуллерен включает пятиугольные и шестиугольные кольца, причем количество пятиугольников всегда равно 12.

Следующая теорема показывает, что это не случайное совпадение. Будем называть степенью вершины количество сходящихся в ней ребер.

Рис. 8.3. Фуллерены и футбольные мячи включают ровно 12 пятиугольников

Эта теорема доказывается прямым применением формулы Эйлера. Предположим, что имеется такой многогранник с P пятиугольными и H шестиугольными гранями. Поскольку у пятиугольника пять сторон, а у шестиугольника — шесть и поскольку каждое ребро является общей границей двух граней, то число ребер равно E = (5P + 6H)/2. С другой стороны, поскольку степень каждой вершины равна 3, то число вершин равно V = (5P + 6H)/3. Подставляя обе величины в формулу Эйлера, получаем

2 = V — E + F = (5P + 6H)/3 — (5P + 6H)/2 + (P + H).

Умножая обе части на 6, приходим к нужному выводу:

12 = 10P + 12H — 15P — 18H + 6P + 6H = P.

У теоремы о двенадцати пятиугольниках есть двойственная формулировка, получаемая заменой граней на вершины и наоборот. Оставляем ее доказательство читателю.

На рис. 8.4 показан пример такого многогранника, где выделено 7 из 12 вершин степени пять. Многие геодезические купола, например Биосфера в Монреале, сконструированы именно так. Разумеется, геодезические купола в архитектуре обычно не являются полными сферами. Тематический парк Эпкот во Всемирном центре отдыха Уолта Диснея имеет такую конструкцию, но каждая треугольная грань разбита еще на три треугольника.

Эти простые примеры позволяют составить первое впечатление о возможностях формулы Эйлера. В последующих главах мы увидим, какая мощь скрывается за элементарным, на первый взгляд, соотношением.

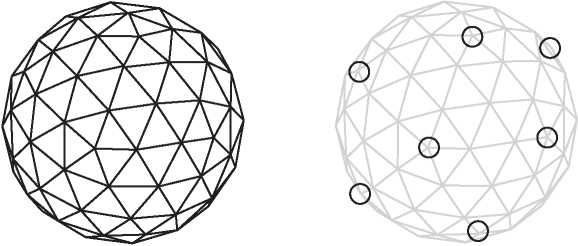
Рис. 8.4. Геодезический купол с двенадцатью вершинами степени пять

Приложения к главе

68. Bell (1945), 211.

69. Poincare (1913), 44.