Скрытая реальность

78

Считается, что учёные должны быть объективны в своих оценках. Но я спокойно отношусь к тому, что мне хотелось бы, чтобы многомировой подход оказался верным, по причине его математической экономичности и далеко идущих последствий для понимания реальности. В то же время, я проявляю здоровый скептицизм, который исходит из трудностей, с которыми сталкивается включение понятия вероятности в этот подход, потому я полностью открыт альтернативным способам решения этого вопроса. Два из них являются хорошим материалом для обсуждения. В одном делается попытка доработать незавершённый копенгагенский подход до полной теории; другой можно рассматривать как многомировой подход, но без множественности миров.

В первом подходе, инициаторами которого являются Джанкарло Джирарди, Альберто Римини и Туллио Вебер, делается попытка придать смысл копенгагенской схеме путём подстройки математического аппарата теории, основанного на уравнении Шрёдингера, так чтобы он действительно приводил к схлопыванию волны вероятности. Но проще сказать, чем сделать. Подстроенный математический аппарат теории не должен изменять волны вероятности объектов микромира, таких как отдельные частицы или атомы, поскольку у нас нет причин вносить поправки в успешное описание явлений в этой области. Но подстройка обязательно требуется, когда в игру вступают объекты макромира, такие как лабораторное оборудование, что приводит к схлопыванию общей волны вероятности. Джирарди, Римини и Вебер развили соответствующий математический аппарат. Итог их работы таков, что с помощью предложенных ими подстроенных уравнений акт измерения действительно заставляет волну схлопнуться; это приводит к эволюции волны вероятности, показанной на рис. 8.6.

Второй подход, изначально развитый Луи де Бройлем в 1920-х годах и затем спустя десятилетия дополненный Дэвидом Бомом, начинается с математического предположения, перекликающегося с идеями Эверетта. Уравнение Шрёдингера при любых обстоятельствах обязано задавать эволюцию квантовых волн. Поэтому в теории де Бройля — Бома волны вероятности распространяются так же, как в многомировом подходе. Однако теория де Бройля — Бома основана на идее, которую я ранее охарактеризовал как ошибочную: в этом подходе все, кроме одного, из множества миров, содержащиеся в волне вероятности, являются лишь возможными мирами; только один мир считается реальным.

С этой целью в данном подходе перестают петь заученную квантовую песню о волне или частице (что до измерения электрон — это волна, а после измерения электрон превращается в частицу), а вместо этого предлагают одновременно рассматривать волны и частицы. В противоположность стандартной квантовой точке зрения, де Бройль и Бом считают частицы крошечными, локализованными сущностями, эволюция которых происходит вдоль определённых траекторий, что приводит к обычной, однозначной действительности, так же как и при классическом описании. Единственный «реальный» мир — это тот, в котором частицы находятся в своих единственных, определённых положениях. При этом квантовые волны играют совершенно другую роль. Вместо воплощения всей совокупности реальностей, роль квантовой волны сводится к руководству движением частиц. Квантовая волна толкает частицы в те положения, где высота волны большая, что делает вероятным обнаружение частиц в этих положениях, и отталкивает от положений, где высота волны мала, что делает обнаружение частиц в этих положениях маловероятным. Для описания этого процесса де Бройлю и Бому требуется дополнительное уравнение, описывающее действие квантовой волны на частицу, поэтому хотя от уравнения Шрёдингера не отказываются, но теперь на сцене появляется и другой математический исполнитель. (Заинтересованный читатель познакомится с этими уравнениями ниже.)

В течение многих лет бытовало мнение, что подход де Бройля — Бома не стоит того, чтобы на него тратить время, что он перегружен дополнительными вещами — не только вторым уравнением, но также, поскольку он вовлекает одновременно частицы и волны, удвоенным списком ингредиентов. Недавно, однако, стали раздаваться голоса, что этот критицизм надо вложить в контекст. Из работы Джирарди — Римини — Вебера совершенно ясно следует, что даже в версии флагмана квантовой механики, в копенгагенском подходе, требуется второе уравнение. Помимо этого, включение как частиц, так и волн приносит огромную выгоду: возрождается понятие объектов, движущихся вдоль определённых траекторий, происходит возвращение к базовому, привычному свойству реальности, от которого копенгагенцы несколько поспешно убедили всех отказаться. На более техническом уровне критицизм состоит в том, что этот подход является нелокальным (новое уравнение показывает, что воздействие в одной точке моментально переносится в удалённые точки), и его трудно совместить со специальной теорией относительности. Но важность первого критического замечания снижается, если заметить, что даже в копенгагенском подходе имеются нелокальные свойства, которые, к тому же, подтверждены экспериментально. Вопрос насчёт совместимости со специальной теорией относительности безусловно важен, и его ещё предстоит решить в полном объёме.

Частично неприятие теории де Бройля — Бома вызвано тем, что математический формализм теории не всегда представляется в отчётливом виде. Для математически настроенного читателя, приведём здесь прямой вывод этой теории.

Начнём с уравнения Шрёдингера для волновой функции частицы:

где плотность вероятности частицы в точке x, ρ(x) задаётся стандартным уравнением,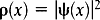

Теперь представьте, что частица движется по определённой траектории со скоростью, задаваемой функцией υ(x) в точке x. Какому физическому условию должна удовлетворять функция скорости? Определённо, она должна удовлетворять закону сохранения вероятности: если частица движется со скоростью υ(x) из одной области в другую, плотность вероятности должна меняться соответственно:

Теперь легко найти решение для υ(x), которое имеет вид

где m — это масса частицы.

Вместе с уравнением Шрёдингера это уравнение определяет теорию де Бройля — Бома. Отметим, что второе уравнение нелинейно, но это не влияет на уравнение Шрёдингера — оно по-прежнему остаётся полностью линейным. Тогда подходящая интерпретация такова, что этот подход для устранения недочётов копенгагенского подхода предлагает новое уравнение, зависящее от волновой функции нелинейным образом. Вся сила и красота основополагающего уравнения, то есть уравнения Шрёдингера, полностью сохраняется.

Можно также добавить, что уравнение непосредственно обобщается на случай многих частиц: в правую часть нового уравнения подставляется волновая функция многочастичной системы ψ(x₁, x₂, x₃… x_n), и при вычислении скорости k-й частицы производная берётся по отношению к k-й координате (рассматривается, для простоты, одномерное пространство; в старших измерениях, соответственно, увеличивается число координат). Это обобщённое уравнение явно нелокально: скорость k-й частицы мгновенным образом зависит от положений других частиц (поскольку волновая функция зависит от координат положения частиц).