Это база: Зачем нужна математика в повседневной жизни

9 Верь мне, я ряд Фурье

В наше время редкий визит к врачу обходится без прохождения обследования с помощью сканера. Эти аппараты бывают разными: магнитно-резонансными, позитронно-эмиссионными, ультразвуковыми… Какие-то из них дают движущиеся изображения в реальном времени, другие используют компьютерные фокусы (то есть математику) для получения трехмерных изображений. Но у всех этих технических чудес есть одно примечательное качество: они позволяют увидеть то, что происходит внутри организма. Не так давно это сочли бы волшебством. Да и сегодня подобное кажется чудом.

В давние времена – а в данном случае эти слова обозначают все, что было до 1895 года, – врачи, исследуя недуги пациентов, вынуждены были полагаться исключительно на собственные чувства и интуицию. Они могли пальпировать тело пациента, чтобы получить представление о форме, размере и положении некоторых внутренних органов; они могли послушать сердцебиение и пощупать пульс; они могли оценить температуру, а также понюхать и попробовать на вкус физиологические жидкости. Но чтобы выяснить, как выглядят внутренности человека, нужно было разрезать его тело. Иногда нельзя было сделать и этого, поскольку религиозные власти нередко запрещали проводить вскрытие, хотя на поле боя это случалось сплошь и рядом, но не в медицинских целях. Допускалось лишь вскрытие людей иной веры.

Новая эпоха началась 22 декабря 1895 года, когда немецкий профессор-физик Вильгельм Рентген сделал снимок руки своей жены, на котором были видны косточки ее пальцев. Снимок был черно-белым, как практически все фотографии того времени, и довольно размытым, но возможность заглянуть внутрь живого организма не имела прецедентов. На жену Рентгена этот снимок, однако, впечатления не произвел. Взглянув на снимок части собственного скелета, она сказала: «Я видела свою смерть».

Рука жены Рентгена на снимке в рентгеновских лучах

Открытие Рентгена можно считать классическим примером счастливой случайности. В 1785 году Уильям Морган провел ряд экспериментов с пропусканием электрического тока через разреженный воздух в запаянной стеклянной трубке и наблюдал слабое свечение, лучше всего заметное в темноте. Свои результаты он представил в Лондонском королевском обществе. К 1869 году физики, экспериментировавшие в модной к тому моменту области разрядных трубок, заметили новое необычное излучение, названное катодными лучами, поскольку оно исходило от катода (отрицательного электрода) трубки. В 1893 году профессор физики Фернандо Санфорд опубликовал статью, посвященную «электрической фотографии». Он соорудил трубку с тонким алюминиевым листом с одного конца и прорезал в этом листе отверстие. При подаче тока то, что вызывало слабое свечение, проходило сквозь это отверстие, попадало на фотопластинку и воспроизводило на ней форму отверстия. Его открытие было описано в прессе – в газете San Francisco Examiner появился заголовок «Без объектива и света, фотографии получены при помощи пластинки и объекта в темноте». Это было поразительно, непонятно и, судя по всему, бесполезно, но физики заинтересовались и стали выяснять, что происходит.

Рентген понял, что странное свечение вызывается каким-то излучением, сходным со светом, но невидимым. Он назвал это излучение X-лучами, где символ X, по освященной временем традиции, указывал на неизвестность его природы. Судя по всему – мы не можем быть в этом совершенно уверены, поскольку записные книжки Рентгена не сохранились, – он случайно обнаружил, что эти лучи способны проходить сквозь лист картона. Это заставило его задаться вопросом о том, сквозь что еще они могут проходить. Сквозь алюминиевую фольгу, очевидно, нет, поскольку на фотографии были видны лишь контуры отверстия. Сквозь книгу – да, сквозь научные статьи – да, сквозь руку жены – да. X-лучи представляли собой беспрецедентное окно, позволявшее заглянуть в живое человеческое тело. Рентген сразу же увидел их медицинский потенциал, и средства массовой информации не замедлили разнести эту новость. В 1896 году журнал Science опубликовал 23 статьи по рентгеновским лучам, а всего в том году этим лучам было посвящено более тысячи научных работ.

Вскоре выяснилось, что рентгеновские лучи хотя и не наносят очевидного ущерба, могут при многократном или длительном воздействии вызывать ожоги кожи и выпадение волос. Как-то раз в лабораторию Университета Вандербилта привезли ребенка, которому выстрелили в голову, и Джон Дэниел сделал рентгеновский снимок его головы с экспозицией в один час. Три недели спустя он заметил на голове ребенка лысинку в том месте, где он размещал рентгеновскую трубку. Несмотря на подобные свидетельства, многие врачи верили в безопасность рентгеновских лучей, а нанесенный ущерб списывали на ультрафиолетовое излучение или озон до тех пор, пока американский рентгенолог Элизабет Флейшман не умерла в 1905 году от осложнений, вызванных рентгеновским излучением. Медицинское использование рентгеновских лучей продолжалось, но с большей осторожностью, к тому же появление более качественных фотографических пластинок позволило снизить время экспозиции. Сегодня мы признаем, что, какими бы полезными для медиков ни были рентгеновские лучи, суммарную дозу излучения следует как можно сильнее ограничивать. Это понимание пришло не сразу. В 1950-е годы, когда мне было около 10 лет, я помню обувные магазины с рентгеновским аппаратом, который позволял при примерке новых туфель посмотреть, насколько хорошо они соответствуют форме ступни.

Недостатков у рентгеновских снимков хватало. Они были черно-белыми: черные области соответствовали тем местам, где лучи не проникали сквозь преграду, белые – тем местам, где проникали, а полутени соответствовали частичной проницаемости материала. Или, чаще, наоборот, поскольку изготовить фотографический негатив всегда проще. Кости были ясно видны, мягкие ткани по большей части не видны. Но самым серьезным недостатком была двумерность изображения. По существу, снимок уплощал внутреннюю картину, и изображения всех органов, располагавшихся между источником рентгеновских лучей и фотопластинкой, накладывались друг на друга. Можно было, конечно, попытаться сделать несколько рентгеновских снимков с разных ракурсов, но в любом случае интерпретация результатов требовала серьезных навыков и опыта, а дополнительные снимки увеличивали дозу радиации.

Возникал вопрос: нельзя ли как-то получить изображение внутренних тканей организма в трех измерениях?

Вообще-то, к тому моменту математики уже сделали несколько фундаментальных открытий, имеющих к этому вопросу непосредственное отношение, и показали, что если сделать множество двумерных «уплощенных» изображений с разных направлений, то можно выстроить трехмерную структуру изображенного объекта. Однако подталкивали их к этому вовсе не рентгеновские лучи и не медицина. Они просто исследовали метод, придуманный для решения задач, связанных с волнами и тепловыми потоками.

Среди действующих лиц этой истории было немало настоящих звезд, начиная с Галилея, который спускал шары по наклонной плоскости и наблюдал восхитительно простые математические закономерности, связывавшие пройденное расстояние и время, и Ньютона, открывшего фундаментальные закономерности движения планет. Ньютон вывел обе закономерности из математических уравнений, описывающих движение системы тел под действием сил. В своем монументальном труде «Математические начала натуральной философии», которые обычно называют просто «Началами», Ньютон объяснял свои идеи через классическую геометрию, но «самая чистая» их математическая формулировка пришла из другого его открытия – дифференциального и интегрального исчисления, которое независимо от Ньютона открыл также Готфрид Вильгельм Лейбниц. При такой интерпретации Ньютон понял, что фундаментальные законы природы можно выразить и другими уравнениями, в которых речь идет о скорости изменения величин во времени. Так, скорость движения объекта есть скорость изменения его положения, или координат, а ускорение объекта есть скорость изменения его скорости.

Закономерности Галилея выглядят проще всего, когда выражены через ускорение: катящийся шар движется с постоянным ускорением. Его скорость, таким образом, увеличивается с постоянной скоростью – возрастает линейно. Его положение определяется равномерно увеличивающейся скоростью, то есть, если шар начинает движение из состояния покоя в момент времени нуль, его координата пропорциональна квадрату прошедшего времени. Ньютон соединил эту идею с другим простым законом об обратной пропорциональности силы тяготения квадрату расстояния и вывел в результате, что планеты движутся по эллиптическим орбитам, объяснив таким образом более ранние эмпирические выводы Иоганна Кеплера.

Математики континентальной Европы ухватились за эти открытия и применили дифференциальные уравнения к широкому спектру самых разных физических явлений. Волны на воде и звуковые волны подчиняются волновому уравнению, электричество и магнетизм тоже имеют собственные уравнения, сильно напоминающие уравнение гравитации. Многие из них являются дифференциальными уравнениями в «частных» производных, которые позволяют соотнести скорость изменений в пространстве со скоростью изменений во времени. В 1812 году Французская академия наук объявила, что темой ее ежегодного призового конкурса будет теплопередача. Нагретые тела остывают, и тепло распространяется через материалы, способные его проводить, – вот почему металлическая ручка кастрюли может сильно нагреться, пока содержимое готовится. Академия хотела получить математическое описание этого процесса, и дифференциальные уравнения в частных производных представлялись вполне правдоподобными кандидатами на решение, потому что распределение теплоты меняется как в пространстве, так и во времени.

Жозеф Фурье отправил в Академию статью о теплопередаче еще в 1807 году, но ее отказались публиковать. Объявленный конкурс вдохновил Фурье на разработку собственного дифференциального уравнения в частных производных для теплопередачи, и это уравнение принесло ему победу. Его «уравнение теплопроводности» утверждает, в математической форме, что теплота в заданном месте изменяется во времени, проникая в соседние области пространства и рассеиваясь в них, как растекается потихоньку капля чернил по промокательной бумаге.

Проблемы начались, когда Фурье попытался решить свое уравнение, начиная с очень простого случая: распространения теплоты по металлическому стержню. Он заметил, что у этого уравнения имеется простое решение, если начальное распределение теплоты выглядит как кривая синуса или косинуса в тригонометрии. Затем он заметил, что, в принципе, можно разобраться и с более сложными вариантами начального распределения, если соединить множество отдельных синусоид и косинусоид. Он даже нашел формулу из дифференциального исчисления, точно описывающую вклад каждого слагаемого: нужно умножить формулу для начального распределения на соответствующий синус или косинус и проинтегрировать результат. Это привело к дерзкому заявлению: его формула, которая в настоящее время называется рядом Фурье, решает задачу совершенно для любого начального распределения теплоты. В частности, утверждал он, формула работает для распределений с разрывами, таких как прямоугольная ступень: полстержня имеет одну постоянную температуру, полстержня – другую.

Это заявление сразу же окунуло Фурье с головой в спор, который шел уже несколько десятилетий. Тот же вопрос – мало того, с той же интегральной формулой – уже всплывал в исследованиях Эйлера и Бернулли, посвященных уравнению волнового движения. Там обычно в качестве любимого примера выступала идеальная скрипичная струна – и понятно, что нельзя заставить струну звучать, нарушив ее непрерывность: она просто порвется. Поэтому физическая интуиция подсказывает, что с представлением функций с разрывами могут возникнуть проблемы, а математическая интуиция усиливает сомнения, заставляя тревожиться о том, сходится ли тригонометрический ряд. То есть имеет ли смысл сумма бесконечного числа синусоидальных кривых, а если имеет, то сойдется ли она в конечном итоге к прямоугольной волне с разрывом или, может быть, к чему-то другому.

Как получить прямоугольный график из синусов и косинусов. Слева: компоненты – синусоидальные волны. Справа: сумма первых пяти членов ряда Фурье аппроксимирует прямоугольный уступ. Дополнительные члены (не показаны) улучшают качество аппроксимации

Не желая никого обижать, замечу, что часть проблемы заключалась в том, что Фурье думал как физик, а его критики – как математики. Физически прямоугольный импульс имеет смысл как модель теплоты. Металлический стержень рассматривается как отрезок идеальной прямой – именно так, кстати говоря, Эйлер и Бернулли рассматривали скрипичную струну. Если теплота распределена равномерно по половине этого отрезка, а вторая половина намного холоднее и перепад между ними резок, то естественной моделью для такого распределения становится прямоугольная ступенька.

Ни одна модель не может быть абсолютно точным представлением реальности, но механика в те дни всегда работала с идеализированными объектами, такими как точечные массы, идеально упругие столкновения, бесконечно тонкие идеально жесткие стержни и т. д. Прямоугольная волна едва ли оказалась бы лишней в такой компании. Более того, математически решение Фурье предсказывает, что нарушение непрерывности сразу же сглаживается диффузией и превращается в резко изгибающуюся, но непрерывную кривую, которая постепенно уплощается, что разумно с физической точки зрения и устраняет математический разрыв. К несчастью, подобные аргументы были слишком неопределенными, чтобы убедить математиков – ведь те знали, что бесконечные ряды часто ставят тонкие и сложные вопросы. Представители Академии пришли к компромиссу: Фурье получил приз, но его работа так и не была опубликована.

Неунывающий Фурье опубликовал эту работу в 1822 году в виде книги «Аналитическая теория теплоты». Затем, чтобы всех подразнить, он умудрился получить должность секретаря Академии и сразу же напечатал свою оригинальную выигравшую приз статью в журнале Академии. Ловко?

Потребовалось около 100 лет, чтобы окончательно разрешить математические вопросы, поднятые заявлениями Фурье. Говоря в целом, он был во многом прав, но ошибался в нескольких принципиальных вопросах. Его метод в самом деле работал для прямоугольного импульса, плюс-минус кое-какие поправки в отношении того, что происходит непосредственно в точке разрыва. Но метод определенно не работал для более сложных начальных распределений. Полное понимание ситуации пришло лишь после того, как математики разработали более общее понятие интеграла, наряду с топологическими понятиями, которые лучше всего формулируются в контексте теории множеств.

Задолго до того, как математическое сообщество разобралось наконец с тем, на что замахнулся Фурье, инженеры ухватились за его базовую идею и, по существу, присвоили ее и начали активно использовать. Они поняли, что сутью его работы было то, что ныне называют преобразованием Фурье, при котором сложный сигнал, изменяющийся во времени, может быть интерпретирован как комбинация простых сигналов с различными частотами. Формула интеграла Фурье подсказывает, как перенести точку наблюдения из временно́й области в частотную и обратно – при этом используется почти та же самая формула, что устанавливает «дуализм» между двумя представлениями.

Этот дуализм означает, что преобразование обратимо, то есть можно восстановить первоначальный сигнал по частотам, которые он создает. Это как перевернуть монету с орла на решку, а затем обратно. Полезность этой процедуры для инженерного дела состоит в том, что некоторые свойства, которые трудно обнаружить во временно́й области, становятся очевидными в частотной области. Это может работать и в обратную сторону, так что мы получаем два очень разных метода анализа одних и тех же данных, и каждый из них естественным образом выявляет именно те черты, которые упускает второй.

Например, реакция высотного здания на землетрясение во временной области кажется случайной и хаотичной. Однако в частотной области можно увидеть несколько больших пиков на определенных частотах. Эти пики позволяют выявить резонансные частоты, которые вызывают особенно сильную реакцию здания. Чтобы здание не рухнуло при землетрясении, необходимо подавить эти частоты. На практике здание ставят на массивное бетонное основание, имеющее возможность двигаться из стороны в сторону. Затем это боковое движение «гасится» гигантскими грузами или пружинами.

Еще одно применение преобразования Фурье восходит к открытию структуры ДНК Фрэнсисом Криком и Джеймсом Уотсоном. Ключевым свидетельством, подтвердившим их правоту, тогда стала фотография дифракции рентгеновских лучей на кристалле ДНК. Для получения такого снимка пучок рентгеновских лучей пропускают сквозь кристалл, который заставляет их отклоняться и отражаться, – такое поведение и называют дифракцией. Волны, как правило, собираются в группы под определенными углами, согласно закону дифракции Лоуренса и Уильяма Брэгга, и на снимке появляется сложная геометрическая композиция из множества точек. Дифракционная картина представляет собой, по существу, своего рода преобразование Фурье позиций атомов в молекуле ДНК. Применив обратное преобразование (сложный расчет, реализовать который сегодня намного проще, чем тогда), можно получить форму молекулы. Как я уже сказал, преобразование иногда делает структурные особенности очевидными, хотя разглядеть их в оригинале довольно трудно. В данном случае опыт работы с другими рентгеновскими дифракционными картинами помог Крику и Уотсону сразу же, без вычисления обратного преобразования, понять, что молекула представляет собой спираль. Другие идеи позволили уточнить это представление, что и привело в конечном итоге к открытию знаменитой двойной спирали, существование которой позже удалось подтвердить при помощи преобразования Фурье.

Это всего лишь два случая практического применения преобразования Фурье и его многочисленной родни. В числе других можно назвать улучшение радиоприема, устранение шума, создаваемого царапинами на старых виниловых пластинках, улучшение эффективности и чувствительности гидролокационных систем, используемых подводными лодками, и устранение нежелательных колебаний в автомобилях на стадии их конструирования.

И все это, как вы можете заметить, не имеет никакого отношения к теплопередаче. Непостижимая эффективность. Главное – это не физическая интерпретация задачи, хотя она вполне могла серьезно повлиять на оригинальную работу, а ее математическая структура. Одни и те же методы применяются при решении задач с одинаковой или похожей структурой, и здесь на сцене появляются сканеры.

Математиков тоже заинтересовало преобразование Фурье, и они перевели его на язык функций. В общем случае функция – это математическое правило превращения одного числа в другое, например «возведение в квадрат» или «извлечение кубического корня». Все традиционные функции, такие как многочлены, корни, экспоненты, логарифмы, и тригонометрические функции (синус, косинус, тангенс) включены в это понятие, но могут существовать и более сложные «правила», которые не выражаются формулами, – взять хотя бы прямоугольный импульс, принесший Фурье так много огорчений.

С этой точки зрения преобразование Фурье берет функцию одного типа (первоначальный сигнал) и преобразует ее в функцию иного типа (список частот). Существует также обратное преобразование, компенсирующее действие прямого. А их двойственность – тот факт, что обратное преобразование почти совпадает с прямым, – представляет собой первоклассный бонус. Корректным контекстом для подобных вещей являются пространства функций с определенными свойствами: функциональные пространства. Гильбертовы пространства, используемые в квантовой теории (глава 6), – это функциональные пространства, где значениями функций являются комплексные числа, а их математика находится в близком родстве с математикой преобразования Фурье.

Математики-исследователи неизменно приобретают устойчивый рефлекс. Когда предлагают новую идею, обладающую замечательными и полезными свойствами, они сразу же задумываются, а нет ли аналогичных идей, которые использовали бы тот же прием в иных обстоятельствах. Существуют ли другие преобразования, подобные преобразованию Фурье? Другие варианты двойственности? Специалисты по теоретической математике ищут ответы на эти вопросы абстрактными и обобщенными способами, тогда как прикладники (а также инженеры, физики и бог знает кто еще) сразу начинают думать о том, как все это можно использовать. В данном случае хитроумный прием Фурье положил начало целой отрасли преобразований и двойственностей, не исчерпавшей свои возможности и по сей день.

Одна из вариаций на тему Фурье открыла нам путь к современным медицинским сканерам. Ее изобретателем был Иоганн Радон. Родился он в 1887 году в городе Течен в Богемии, области Австро-Венгрии (ныне это Дечин в Чешской Республике). По всем отзывам это был дружелюбный и симпатичный человек, спокойный, воспитанный и легко сходившийся с другими. Подобно многим ученым и людям свободных профессий, он любил музыку, а в те времена, до появления радио и телевидения, люди часто собирались у кого-нибудь дома и музицировали. Радон хорошо играл на скрипке и прекрасно пел. Как математик, он поначалу работал над вариационным исчислением – именно ему была посвящена его докторская диссертация – и естественным образом переключился на новую быстро растущую область функционального анализа. В этой области, начало которой положили польские математики под руководством Стефана Банаха, ключевые идеи классического анализа интерпретировались заново с точки зрения функциональных пространств бесконечной размерности.

На начальном этапе развития математического анализа математики сосредоточивались на вычислении таких вещей, как производная функции, то есть скорость ее изменения, и ее интеграл, то есть площадь под графиком функции. С развитием предмета фокус сместился на общие свойства операций дифференцирования и интегрирования и на то, как они ведут себя в случае комбинации функций. Если сложить две функции, что произойдет с их интегралами? На передний план вышли особые свойства функций. Непрерывна ли функция (нет ли у нее скачков)? Дифференцируема ли она (плавно ли изменяется)? Интегрируема ли (имеет ли смысл площадь)? Как связаны друг с другом эти свойства? Как все это работает, если взять предел последовательности функций или сумму бесконечного ряда? Какого рода предел или сумму?

Банах и его коллеги сформулировали эти более общие вопросы с точки зрения «операторов». Точно так же, как функция превращает одно число в другое, оператор превращает функцию в число или в другую функцию. Примеры – «взять интеграл» или «продифференцировать». Польские и другие математики обнаружили, что можно взять теоремы о числовых функциях и превратить их в теоремы об операторах функций. Получившееся в результате утверждение может быть истинным, а может и не быть: самое интересное здесь – понять, что, собственно, происходит. Идея получила развитие, потому что довольно скучные теоремы о функциях превращаются в очевидно более глубокие теоремы об операторах, но при этом доказать их зачастую можно теми же простыми методами. Еще один прием состоял в отбрасывании формальных вопросов о том, как интегрировать сложные формулы с синусами, логарифмами и т. п., и в переосмыслении основ. Чем на самом деле занимается математический анализ? Самым фундаментальным вопросом анализа оказалось измерение близости двух чисел. Она определяется разностью между ними в том порядке, который позволяет сделать разность положительной. Функция непрерывна, если маленькая разность между числами на входе дает маленькую разность между числами на выходе. Чтобы найти производную функции, нужно увеличить переменную на маленькую величину и посмотреть, как меняется значение функции в пропорции к этой маленькой величине. Чтобы играть в подобные игры на следующем уровне, с операторами, следует определить, что означает близость между двумя функциями. Сделать это можно множеством способов. Можно посмотреть на разность их значений в любой заданной точке и сделать так, чтобы эта разность была маленькой (во всех точках). Можно сделать интеграл этой разницы маленьким. Каждый вариант ведет нас к иному «функциональному пространству», содержащему все функции с заданными свойствами и снабженному собственной «метрикой» или «нормой». Если вернуться к аналогии между числами и функциями, то функциональное пространство играет роль множества действительных или комплексных чисел, а оператор – это правило преобразования функции из одного функционального пространства в функцию из другого функционального пространства. Преобразование Фурье – особенно важный пример оператора, преобразующего функцию в последовательность коэффициентов Фурье. Обратное действие преобразует последовательности чисел в функции.

С этой точки зрения большие фрагменты классического анализа внезапно становятся частью единой картины как примеры функционального анализа. Функции одной или нескольких действительных или комплексных переменных можно рассматривать как довольно простые операторы на довольно простых пространствах – на множестве действительных чисел, множестве комплексных чисел или векторных пространствах конечной размерности, образованных последовательностями таких чисел. Функция трех переменных – это всего лишь функция, или оператор, определенная на пространстве всех троек действительных чисел. Более заумные операторы, такие как «проинтегрировать», определены на (скажем) пространстве всех непрерывных функций, переводящих трехмерное пространство в пространство действительных чисел, с метрикой «интегрировать квадрат разности значений двух функций, о которых идет речь». Основное различие здесь в пространствах: пространство действительных чисел и трехмерное пространство имеют конечную размерность, а размерность пространства всех непрерывных функций бесконечна. Функциональный анализ во всем похож на обычный математический анализ, но применяемый к пространству бесконечной размерности.

Еще одна крупная инновация того периода тоже аккуратно встала на свое место в этой картине: это новая, более общая и более гибкая теория интегрирования, предложенная Анри Лебегом под названием «теория меры». Мера – это величина вроде площади или объема, позволяющая присвоить число множеству точек в пространстве. Интересная особенность здесь в том, что это множество может быть чрезвычайно сложным, хотя некоторые множества настолько сложны, что даже концепция меры Лебега к ним неприменима.

Вариационное исчисление, тема диссертации Радона, буквально «кричит» об операторах, как только мы видим, что речь в нем идет о поиске функций (не чисел) с оптимальными свойствами. Так что для Радона отход от классического вариационного исчисления и погружение в функциональный анализ были вполне естественным шагом. Это привело его к большому успеху – несколько важных идей и теорем в теории меры и функциональном анализе названы в его честь.

Среди них преобразование Радона, на которое он наткнулся в 1917 году. С точки зрения функционального анализа оно – близкий математический родственник преобразования Фурье. Для начала берется изображение на плоскости, которое рассматривается как черно-белая картинка с областями, окрашенными в различные оттенки серого. Любой оттенок может быть представлен действительным числом от 0 (черный) до 1 (белый). Можно сжать изображение в линию в любом направлении, сложив при этом числа, представляющие темные и светлые области и получив проекцию изображения. Преобразование Радона охватывает все эти сжатые проекции во всех направлениях. По-настоящему важная идея – обратное преобразование, позволяющее восстановить первоначальное изображение по этим проекциям.

Насколько я могу судить, Радон изучал свое преобразование из чисто математических соображений. В его статье, посвященной преобразованию, не упоминается какое-либо его практическое применение. Ближе всего к реальной жизни подходит краткое упоминание о связи преобразования с математической физикой, а именно с теорией потенциала, где сходятся электричество, магнетизм и тяготение. Радона, кажется, куда больше интересовала математика и возможные обобщения. В более поздней работе он исследовал трехмерный аналог этого преобразования, в котором распределение светлых и темных областей в пространстве сжимается до плоскости во всех возможных направлениях, и нашел формулу восстановления для этой операции. Позже другие математики отыскали обобщения для более высоких размерностей. Радон мог ориентироваться на рентгеновские лучи, которые порождают именно такого рода проекции органов и костей в человеческом теле: «светлое» и «темное» здесь интерпретируются как разница в прозрачности для рентгеновских лучей. Но потребовалось целое столетие, чтобы его открытие нашло применение в устройствах, способность которых зондировать внутренности человека кажется почти чудесной.

Аппараты компьютерной томографии (КТ) используют рентгеновские лучи для создания трехмерных изображений внутренностей человека. Эти изображения хранятся в компьютере, ими можно манипулировать, чтобы показывать кости и мышцы или чтобы обнаруживать раковые опухоли. Широко используются и другие типы сканеров, например ультразвуковые. Но как сканер выясняет, что находится внутри нашего тела, не вскрывая его? Мы все знаем, что рентгеновские лучи легко проходят сквозь мягкие ткани, тогда как более плотные ткани, например кости, менее проницаемы для них. Но рентгеновское изображение, полученное с определенного направления, показывает только среднюю плотность тканей на пути луча. Как подобный снимок превратить в трехмерное изображение? Радон начинает свою статью с заявления о том, что ему удалось решить эту проблему:

Ответ – обратное преобразование Радона, то есть формула, восстанавливающая внутреннее распределение тканей (точнее говоря, степени их непроницаемости для рентгеновских лучей) по множеству проекций со всех направлений.

Чтобы понять, как это работает, для начала опишем, что можно увидеть на единственном скане (проекции) тела. Такой скан берется на одном двумерном срезе тела. На картинке схематически изображены параллельные рентгеновские лучи, проходящие через срез тела, содержащий несколько внутренних органов с разной степенью непроницаемости для рентгеновских лучей. Проходя сквозь эти органы, лучи меняют интенсивность. Чем более непроницаем орган, встретившийся на пути луча, тем ниже интенсивность луча на выходе. Мы можем построить график изменения наблюдаемой интенсивности в зависимости от положения луча.

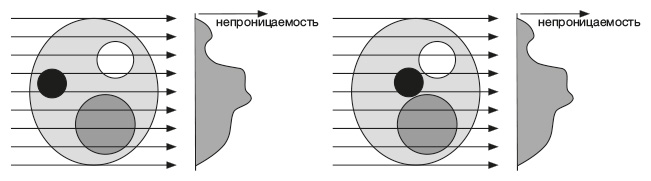
Чем темнее область, тем менее она проницаема. Слева: сканирование единичного среза тела с одного направления дает график наблюдаемой непроницаемости для рентгеновских лучей только в этом направлении. Справа: другое распределение внутренних тканей дает тот же самый график

В результате одно изображение такого рода сжимает распределение серого внутри тела вдоль направления луча в точку. Технически мы получаем проекцию распределения в этом направлении. Понятно, что одна проекция такого рода не может сказать в точности, как расположены органы внутри тела. Например, если сдвинуть черный орган в направлении луча, проекция не изменится. Однако если сделать еще один скан, рассматривая тело в вертикальном направлении, то изменение положения черного кружочка будет заметно на графике непроницаемости. Интуитивно понятно, что можно получить еще больше информации о пространственном расположении органов и тканей, сделав серию сканов, слегка повернутых относительно друг друга. Но достаточно ли будет информации, чтобы определить положение всех значимых деталей в точности?

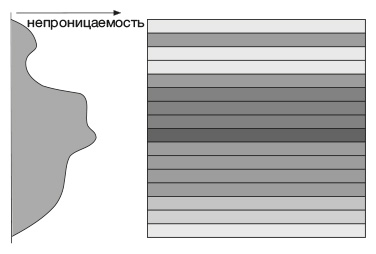
Превращение графика непроницаемости в серию полос, окрашенных в оттенки серого и выстроенных в направлении рентгеновского луча

Как доказал Радон, если имеются графики непроницаемости для случаев, когда срез тела рассматривается со всех возможных направлений, то можно определить двумерное черно-белое распределение тканей и органов в точности. Мало того, существует очень простой способ сделать это – обратная проекция. Он позволяет как бы размазать черно-белое распределение вдоль направления луча, причем размазать однородно. Так что мы получаем квадратную область, заполненную серыми полосками разных оттенков. Чем выше в данном месте график, тем темнее получается полоска. Мы интуитивно размазываем серый цвет вдоль полоски, поскольку не можем определить из одной проекции, где именно располагаются конкретные внутренние органы.

Мы можем проделать эту операцию для каждого направления оригинальной серии сканов. Обратная формула Радона говорит, что, если наклонить все эти полосатые картинки на соответствующий угол и наложить друг на друга, так чтобы в каждой точке оттенки серого сложились, то результат – надлежащим образом отмасштабированный – покажет первоначальное распределение внутренних органов. На следующем рисунке видно, как это работает, если первоначальное изображение – квадрат и мы восстанавливаем его при помощи обратной проекции с нескольких (от 5 до 100) направлений. Чем больше направлений, тем лучше результат.

Слева: квадрат. В середине: обратная проекция с пяти направлений. Справа: обратная проекция со 100 направлений[8]

Восстановив распределение тканей в одном срезе, мы сдвигаем тело вдоль оси прибора на небольшое расстояние и проделываем эту же операцию еще раз. И еще, и еще, пока не нарежем тело условными плоскостями на ломти, как батон внарезку. После этого можно собрать ломтики, сложить их в компьютере и получить полное описание трехмерного распределения тканей. Этот метод определения трехмерной структуры по серии двумерных срезов известен как томография и давно используется микроскопистами, поскольку позволяет заглянуть внутрь твердых объектов, таких как насекомые или растения. Объект при этом заливают воском, а затем отрезают от него тончайшие ломтики при помощи устройства, похожего на миниатюрную машинку для нарезки колбасы и называемого микротомом (от греческих слов micros – «маленький» + temnein – «резать»). КТ-сканеры используют эту же идею, разве что «нарезку» здесь производит не микротом, а рентгеновские лучи при помощи математических фокусов.

После этого остается только прибегнуть к рутинным математическим методам обработки трехмерных данных и получения всевозможной информации. Мы можем посмотреть, как выглядели бы ткани на сечении, взятом под совершенно другим углом, или показать только ткани определенного типа, или обозначить условными цветами мышцы, органы и кости. В общем, любые украшательства, на ваш вкус. Главные инструменты здесь – стандартные методы обработки изображений, опирающиеся в конечном итоге на трехмерную координатную геометрию.

На практике все далеко не так просто. Сканер, конечно, делает не бесконечное число снимков с непрерывного множества направлений, а просто большое конечное их число с близких дискретных направлений. Алгоритмы математической обработки приходится модифицировать, чтобы учесть этот факт. Полезно, например, фильтровать данные, чтобы избежать помех на изображении, возникающих в результате использования дискретного множества направлений. Но базовый принцип остается тем же, что выработал Радон более чем за 50 лет до изобретения первого сканера. Английский инженер-электрик Годфри Хаунсфилд построил первый работоспособный сканер в 1971 году. Теорию разработал в 1956–1957 годах американский физик южноафриканского происхождения Аллан Кормак, а опубликована она была в 1963–1964 годах. В то время Кормак не знал о результатах Радона, так что он вывел все, что требовалось, самостоятельно, но позже наткнулся на статью Радона, которая носит более общий характер. Разработка метода и прибора для компьютерной томографии принесла Хаунсфилду и Кормаку в 1979 году Нобелевскую премию по физиологии и медицине. Их аппарат стоил $300. Сегодня стоимость коммерческого КТ-сканера составляет порядка $1,5 млн[9].

Сканеры используются не только в медицине. Египтологи, например, теперь привычно прибегают к их помощи при изучении мумий. Они могут осмотреть скелет и оставшиеся внутренние органы, поискать признаки переломов и болезней и выяснить, где спрятаны религиозные амулеты. Музеи часто добавляют в свои экспозиции виртуальные мумии, снабдив их тачскрином, которым могут управлять посетители: они могут сами снять полотняные пелены слой за слоем, затем удалить кожу, затем мышцы, пока не останутся одни кости. Все это делается при помощи математики, воплощенной в компьютере: трехмерная геометрия, обработка изображения, методы отображения графической информации.

Существует немало и других типов сканеров. Есть ультразвуковые аппараты; аппараты позитронно-эмиссионной томографии (ПЭТ), регистрирующие элементарные частицы, испускаемые радиоактивными веществами, которые вводятся в организм; магнитно-резонансные томографы (МРТ), регистрирующие магнитные эффекты в ядрах атомов. Последние одно время называли сканерами на эффекте ядерного магнитного резонанса (ЯМР), пока рекламщики не сообразили, что слово «ядерный» может отпугивать людей. И у каждого типа сканера своя математическая история.