Это база: Зачем нужна математика в повседневной жизни

6 Числовая плоскость

В нашем районе города Ковентри в последние месяцы наблюдается какая-то непонятная, но активная деятельность. Всюду вдоль обочин виднеются припаркованные белые автобусы, часто в сопровождении грузовиков с лопатами и тачками. Мини-экскаваторы ездят туда-сюда по улицам, копают канавы вдоль тротуаров, поперек дорог, через газоны и скверы, а полосы свежеуложенного асфальта тянутся во все стороны, подобно следам, оставленным слизнями размером с собаку. Люди в куртках со светоотражающими элементами то и дело ныряют в колодцы с открытыми люками. Катушки с кабелем красуются на газонах, притулившись к живым изгородям, и ждут, когда кабель засосет в колодцы. Сосредоточенные инженеры сидят под навесами от дождя и разбираются с тысячами разноцветных проводов в больших металлических ящиках.

На бортах автобусов имеется надпись, объясняющая происходящее: «Сверхбыстрая широкополосная связь уже в вашем районе».

В центры крупных городов Великобритании это чудо современных телекоммуникаций пришло уже давно, но наш дом находится на тихой окраине. Как-то к нам даже отказались ехать по вызову, потому что мы живем слишком далеко – на расстоянии целых пяти километров. Справедливости ради замечу, что граница города проходит всего в нескольких сотнях метров от нас. Прокладка кабелей здесь стоит дороже, а плотность населения меньше, потому что сразу за границей города начинаются фермерские поля. Здесь нет возможности легкого расширения с минимальными затратами. Мы просто не были привлекательным предложением. Но в конечном итоге, после того как правительство надавило на телекоммуникационные корпорации, началось повсеместное подключение к оптико-волоконным линиям всех городских и большинства сельских районов. Наконец, остальная страна начала догонять районы с максимальной плотностью населения, где подключение к интернету становится все быстрее и быстрее. Отставание как минимум перестало расти.

В век, когда чуть ли не все виды деятельности перебираются, хотя бы частично, в интернет, быстрая широкополосная связь из роскоши превратилась в жизненную необходимость. Может быть, не настолько жизненную, как вода или электричество, но уж никак не менее важную, чем телефон. Хитроумная электроника – движитель компьютерной революции и систем быстрой всемирной связи – сделала мир 2020-х годов таким, какой невозможно было представить еще в 1990-е годы. И это только начало. Расширение предложения вызывает взрывной рост спроса. Дни, когда телефонные линии представляли собой медные провода и передавали голосовые сообщения, быстро уходят в прошлое, да и домашние телефоны в последние годы работают только благодаря хитроумным электронным и математическим фокусам, позволяющим повысить пропускную способность. Сегодня телекоммуникационные кабели передают куда больше цифровых данных, чем разговоров. Именно поэтому на передний план вышло оптическое волокно.

Пройдет еще несколько десятилетий, и оптоволокно так же устареет, как устарели в свое время лошади и повозки. На очереди другие новинки, которые позволят передавать намного большие объемы данных с захватывающей дух скоростью. Некоторые из них уже существуют. Классическая физика электричества и магнетизма остается фундаментальной наукой, но инженеры-электронщики, занимаясь проектированием следующего поколения телекоммуникационных устройств, все больше обращаются к странному квантовому миру. В фундаменте как классической физики, так и квантовой механики, на которых основываются все новые разработки, лежит одна из самых любопытных математических находок в истории. Ее истоки можно проследить аж до Древней Греции, в эпоху итальянского Возрождения она только проклевывалась, а расцвела уже в XIX веке, когда стремительно захватила большую часть математики. Ее широко использовали задолго до того, как стало по-настоящему понятно, что это такое.

Я называю это находкой, а не открытием, потому что здесь воображение математиков не вдохновлялось миром природы. Если эта штука и присутствовала где-то, ожидая, пока ее обнаружат, то это было очень странное место – мир человеческого воображения, правил логики и структуры. Это был новый тип числа, настолько новый, что это число получило название «мнимое». Такое название используется и сегодня, и для большинства из нас мнимые числа остаются совершенно чужеродной сущностью, хотя наша жизнь все больше от них зависит.

Вы, конечно, слышали о числовой прямой.

Познакомьтесь теперь с числовой плоскостью.

Чтобы понять, откуда взялась эта странная находка, а также почему она появилась, нужно сначала взглянуть на традиционные типы чисел. Числа – это настолько обычно, настолько знакомо, что очень легко недооценить все их тонкости. Мы знаем, что два плюс два будет четыре, а пятью шесть – тридцать. Но что такое «два», «четыре», «пять», «шесть» и «тридцать»? Это не слова: в разных языках для обозначения одних и тех же чисел используются разные слова. Это не символы 2, 4, 5, 6, 30: в разных культурах используются разные символы. В двоичной записи, которой пользуются в компьютерных делах, эти числа выглядят как 10, 100, 101, 110 и 11110. А что такое символ?

Все было гораздо проще, когда число рассматривалось как непосредственное описание природы. Если у вас десять овец, то число десять есть заявление о том, сколько именно у вас овец. Если вы продали четыре из них, у вас останется шесть. Числа представляли собой, по существу, средство счета. Но когда математики стали использовать числа все более заумными способами, этот прагматический взгляд начал казаться довольно шатким. Если вы не знаете, что такое числа, то разве можете быть уверены, что ваши расчеты никогда не будут противоречить друг другу? Если фермер пересчитает одну и ту же отару овец дважды, – обязательно ли результат будет одинаковым? Кстати, что мы имеем в виду, когда говорим «пересчитает»?

В XIX веке «придирки» такого рода начали возникать, потому что к тому моменту математики успели уже не единожды расширить концепцию числа. Каждая новая версия включала в себя все, что было раньше, но связь с реальностью при этом становилась все менее явной. Сначала на сцене были только натуральные, или счетные, числа 1, 2, 3….. Далее появились дроби, такие как 1/2, 2/3 или 3/4. В какой-то момент в ряды чисел тихонько проскользнул нуль. До этого соответствие с реальностью было, в общем-то, непосредственным: возьмите два апельсина и еще три апельсина и сосчитайте их все, чтобы убедиться, что всего у вас оказалось пять апельсинов. Взяв кухонный нож, я могу наглядно продемонстрировать вам пол-апельсина. Ну а нуль апельсинов? Ну, это пустое место.

Даже здесь уже наблюдаются сложности. Пол-апельсина – это, строго говоря, не число апельсинов. Это вообще не апельсин, а всего лишь его кусок. Существует множество способов разрезать апельсин пополам, и не все они выглядят одинаково. Проще показывать на кусках веревки – при условии, что мы режем веревку на части очевидным способом и не делаем никаких глупостей, например не расплетаем ее на пряди и волокна. Здесь снова все просто. Длина одной веревки равна половине длины другой, если две веревки, равные по длине первой, при соединении друг с другом имеют длину, равную длине второй. Дроби лучше всего работают с измерением разных вещей. Древние греки считали, что с измерениями работать легче, чем с числовыми символами, поэтому Евклид повернул эту идею задом наперед. Вместо того чтобы использовать числа для измерения длины отрезка, он использовал отрезки для представления чисел.

Следующий шаг – отрицательные числа – несколько сложнее, поскольку мы не можем наглядно продемонстрировать минус четыре апельсина. С деньгами проще, там отрицательное число можно интерпретировать как долг. Все это понимали в Китае около 200 года, о чем свидетельствует первый известный нам письменный источник «Математика в девяти книгах», хотя сама идея, несомненно, намного старше. Когда числа ассоциируют с измерениями, интерпретации отрицательных величин возникают совершенно естественно. Например, отрицательную температуру можно интерпретировать как температуру ниже нуля, тогда как положительная температура выше нуля. В некоторых случаях положительные измерения лежат справа от некоторой точки, тогда как отрицательные – слева, и т. д. Отрицательное противоположно положительному.

В наши дни математики уделяют много внимания различиям между этими типами числовых систем, но для обычного пользователя все они являются вариантами одной темы: это числа. Мы с готовностью принимаем такую довольно наивную договоренность, поскольку во всех этих системах работают одни и те же правила арифметики и каждый новый тип чисел просто расширяет старую систему, ничего не меняя в том, что нам известно. Преимущество расширения концепции числа состоит в том, что каждый раз появляется возможность производить «арифметические действия», недоступные прежде. В натуральных числах мы не можем разделить 2 на 3, в дробях – можем. В натуральных числах мы не можем вычесть 5 из 3, в отрицательных числах – можем. Все это делает математику проще, потому что можно перестать беспокоиться о том, разрешены те или иные арифметические операции или нет.

Дроби позволяют делить разные вещи на сколь угодно мелкие части. Мы можем разделить метр на миллиметры, составляющие одну тысячную долю его длины, или на микрометры, составляющие одну миллионную, или на нанометры (это уже одна миллиардная) и т. д. Названия у нас закончатся намного раньше, чем нули. Практические измерения никогда не обходятся без небольших ошибок, поэтому дробей нам вполне достаточно для всех целей. Мало того, мы можем обойтись только дробями со знаменателем, равным степени десяти, – посмотрите на любой электронный калькулятор. Но для важных теоретических целей, а также для сохранения порядка в математике дробей, как оказалось, не хватает.

Последователи древнегреческого культа пифагорейцев верили, что Вселенная управляется числами (кстати, подобные взгляды до сих пор преобладают в самой передовой физике, хотя и не в столь буквальном виде). Пифагорейцы признавали только натуральные числа и положительные дроби, поэтому их система взглядов была потрясена до основания, когда один из них обнаружил, что длина диагонали квадрата не равна точной доле длины его стороны. Это открытие привело к появлению так называемых иррациональных чисел, в данном случае к квадратному корню из двух. В результате сложной исторической эволюции, начавшейся в Китае в IV веке до н. э. и продолжавшейся до Симона Стевина в 1585 году, такие числа стали представлять в виде десятичных дробей:

Поскольку это число иррациональное, оно должно продолжаться бесконечно и не заканчиваться одними только нулями. Оно не может даже повторять одну и ту же группу цифр снова и снова, как 1/3, которая в десятичной записи равна 0,333333333… Это «бесконечная десятичная дробь». Мы не в состоянии записать ее целиком, но теоретически можем делать вид, что это возможно, потому что, в принципе, можно продолжать запись как угодно долго.

Несмотря на необходимость прибегать к бесконечному процессу, бесконечные десятичные дроби обладают очень приятными математическими свойствами, в частности позволяют точно записать геометрические длины, такие как √2, которые в противном случае не имели бы численных значений. Бесконечные десятичные дроби получили название действительных чисел, поскольку представляли собой (идеализированные) измерения реальных величин, таких как длина, площадь, объем и вес. Каждая последовательная цифра в них представляет кратное некоторого базового размера, который на каждом шаге уменьшается в 10 раз. Можно считать, что эта процедура продолжается бесконечно, причем базовые размеры становятся все меньше и меньше. Это позволяет нам представить нужное число с какой угодно точностью. Реальная физика на атомном уровне не такова, да и само пространство, вероятно, тоже не такое, но действительные числа необычайно хорошо представляют реальность в очень многих случаях.

Исторически новые типы чисел, как правило, поначалу встречали сопротивление. Затем, когда их полезность становилась очевидной, а использование – привычным, общее отношение к ним менялось. На протяжении жизни одного поколения сопротивление в основном исчезало: если вы с детства привыкли регулярно чем-то пользоваться, то оно кажется вам совершенно естественным. Философы могли и дальше спорить, является ли нуль числом – у них и сегодня нет единого мнения в этом вопросе, – но обычные люди уже пользовались им при необходимости и перестали гадать, что это на самом деле. Даже математики вели себя так, хотя и испытывая иногда чувство вины. Можно отметить, что терминология выдает эту игру: новые числа называются не как-нибудь, а отрицательными, иррациональными и т. п.

Однако даже у математиков некоторые инновации вызывали головную боль, которая не проходила столетиями. Но что по-настоящему нарушило спокойствие математического сообщества, так это введение так называемых мнимых чисел. Даже название (которое до сих пор используется исключительно по привычке) указывает на вызванную ими степень ошеломления и намекает, что репутация у этих чисел по какой-то причине была довольно сомнительная. Опять же в основе их лежали квадратные корни.

Стоило нам расширить числовую систему так, чтобы она включала в себя бесконечные десятичные дроби, как выяснилось, что у каждого положительного числа есть квадратный корень. Мало того, два квадратных корня: один положительный, другой отрицательный. Например, у числа 25 два квадратных корня: +5 и –5. Этот любопытный факт является следствием правила «минус на минус дает плюс», которое при первом знакомстве часто ставит людей в тупик. Некоторые в принципе не в состоянии его принять. Однако это простое следствие принципа, согласно которому отрицательные числа должны подчиняться тем же арифметическим правилам, что и положительные. Это звучит разумно, но подразумевает, что у отрицательных чисел не бывает квадратных корней. Так, у числа –25 нет квадратных корней. Это кажется несправедливым, если вспомнить, что у его родича, числа +25, таких корней целых два. Поэтому математики долгое время рассуждали о новом цифровом царстве, где у отрицательных чисел тоже имеются квадратные корни. При этом они молчаливо подразумевали, что в нем обычные правила арифметики и алгебры продолжают действовать. Позднее стало очевидно, что для появления такого царства необходимо всего одно принципиально новое число: квадратный корень из минус единицы. Это новое число получило обозначение i, которым и сегодня пользуются все, кроме инженеров (они используют символ j). Воспользовавшись этим обозначением, можно без труда записать его ключевое свойство:

Теперь в числовом царстве правит справедливость, и каждое число, положительное или отрицательное, имеет два квадратных корня{48}. Исключение составляет нуль, поскольку –0 = +0, но нуль часто становится исключением, поэтому никого это не смущает{49}.

Идею о том, что отрицательное число может, в принципе, иметь осмысленный квадратный корень, можно проследить до древнегреческого математика и механика Герона Александрийского, но первые шаги к разумной реализации этой идеи были сделаны лишь полтора тысячелетия спустя в Италии в эпоху Возрождения. Джероламо Кардано упомянул такую возможность в своем трактате «Великое искусство» (одном из первых алгебраических трудов) в 1545 году, но затем отбросил эту идею как бессмысленную. Прорыв произошел в 1572 году, когда итальянский алгебраист Рафаэль Бомбелли сформулировал правила для вычислений с гипотетическим квадратным корнем из минус единицы и нашел действительные решения одного кубического уравнения с использованием формулы, где складывались два «числа», которые никак не могли быть действительными. Невозможные части успешно сократились друг с другом, оставив вполне корректный – действительный – ответ. Этот дерзкий мудреный фокус заставил математиков спохватиться, потому что полученные решения можно было проверить непосредственно и они работали.

Чтобы подсластить пилюлю, новые числа стали называть мнимыми, в противовес традиционным действительным, которые можно было использовать для измерения реальных объектов. Эта терминология незаслуженно наделяла действительные числа особым статусом и, кроме того, смешивала математическую концепцию и общепринятый способ ее использования. Как мы увидим, у мнимых чисел тоже есть полностью осмысленные применения и интерпретации, но не в качестве измерений привычных физических величин вроде длины или массы. Бомбелли первым продемонстрировал, что мнимые числа – чем бы они ни были – можно использовать для решения совершенно реальных задач. Это как если бы фантастический плотницкий инструмент, даже не существующий в реальности, можно было взять и использовать для изготовления совершенно нормального стула. Конечно, это был концептуальный стул, но сам процесс все равно выглядел непостижимо. Еще более непостижимо выглядели свидетельства того, что все это работает.

Все это чудесным образом продолжало работать в постоянно расширяющемся спектре областей. К XVIII веку математики уже свободно пользовались новыми числами. В 1777 году Эйлер ввел для обозначения квадратного корня из минус единицы стандартный символ i. Комбинация действительных и мнимых чисел привела к созданию красивой и непротиворечивой системы, известной как комплексные числа, то есть «составленные из нескольких частей», а не «сложные». Алгебраически они выглядят как a + bi, где a и b – действительные числа. Комплексные числа можно складывать, вычитать, перемножать, делить, извлекать из них квадратные, кубические и прочие корни, не выходя при этом за пределы системы.

Главный недостаток комплексных чисел – то, что для них трудно подобрать интерпретацию в реальном мире, по крайней мере в то время все так думали. Неясно, при измерении чего и каким образом может быть получен результат, равный, скажем, 3 + 2i. Квазифилософские дебаты о легитимности комплексных чисел бушевали до тех пор, пока математики не поняли, как эти числа можно использовать для решения задач в области математической физики. Поскольку ответы здесь можно проверить другими средствами и они, кажется, всегда верны, споры отошли на задний план, уступив место ажиотажу и поспешному исследованию новых методов.

Долгое время математики пытались оправдать существование мнимых чисел, апеллируя к масштабному, но довольно туманному принципу перманентности, в соответствии с которым любое алгебраическое правило, верное для действительных чисел, должно автоматически распространяться и на комплексные числа. Главным доказательством этого утверждения считался тот факт, что на практике использование комплексных чисел давало правильные ответы, – по существу, триумф надежды над логикой. Короче говоря, они работали, потому что работали, и доказательством служило то… что они работали.

Лишь много позже математики разобрались в том, как можно представлять комплексные числа. Надо сказать, что они, подобно отрицательным числам, имеют несколько «физических» интерпретаций. Мы вскоре увидим, что в электротехнике комплексное число сочетает в себе амплитуду (максимальную величину) переменного сигнала и его фазу в одном компактном и удобном пакете. То же происходит и в квантовой механике. Если взять более прозаический пример, то как действительные числа соответствуют точкам на прямой, так комплексные числа соответствуют точкам на плоскости. Очень просто. И, как многие другие простые идеи, эта идея оставалась незамеченной несколько столетий.

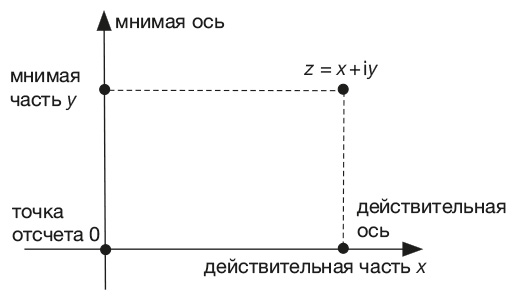
Комплексная числовая плоскость

Первый намек на этот прорыв можно увидеть в «Алгебре» Джона Уоллиса 1685 года. Автор распространил общепринятое представление действительных чисел в виде прямой на комплексные числа. Предположим, что некое число равно a + bi. «Действительная часть» a – это просто действительное число, так что мы можем расположить его на обычной действительной прямой, которую можно представить как фиксированную прямую на плоскости. Второй компонент bi – это мнимое число, поэтому у него нет соответствующей ему точки на числовой прямой. Однако коэффициент b – действительное число, так что мы можем провести отрезок длиной b на той же плоскости, под прямым углом к действительной прямой. Точка на этой плоскости, полученная таким образом, представляет число a + bi. Сегодня мы сразу же видим, что это число представлено на плоскости точкой с координатами (a, b), но в то время предложение Уоллиса не встретило понимания. Исторически честь изобретения комплексной плоскости чаще всего достается Жан-Роберу Аргану, который опубликовал свое предложение в 1806 году, но на самом деле малоизвестный датский топограф Каспар Вессель чуть-чуть опередил его, опубликовав аналогичную идею в 1797 году. Однако статья Весселя была написана по-датски и оставалась никем не замеченной, пока столетие спустя не был сделан ее перевод на французский. Оба автора привели в своих статьях геометрические построения в евклидовом стиле, показывающие, как следует складывать и перемножать любые два комплексных числа.

Наконец в 1837 году ирландский математик Уильям Роуэн Гамильтон прямо указал, что можно представить любое комплексное число в виде пары действительных чисел – координат точки на плоскости:

Затем он записал геометрические построения в виде двух формул для сложения и перемножения таких пар. Я покажу их здесь, потому что они довольно просты и элегантны:

Это может показаться немного непонятным, но работает прекрасно. Числа вида (a, 0) ведут себя в точности как действительные числа, а загадочное i соответствует паре (0, 1) – именно Уоллис предложил располагать мнимые числа под прямым углом к действительным и записывать как координаты. Формулы Гамильтона гласят:

что мы уже распознали как действительное число –1. Дело сделано. Естественно, после этого выяснилось, что Гаусс упоминал эту идею в письме к Вольфгангу Бойяи в 1831 году, но не опубликовал ее.

Если Гаусс, похоже, не понимал до конца, то Гамильтон точно видел возможность доказать с помощью этих двух формул, что комплексные числа подчиняются обычным законам алгебры, таким как перестановочный xy = yx и сочетательный (xy)z = x(yz) законы, которые большинство из нас воспринимает как само собой разумеющиеся при первом знакомстве с алгеброй. Чтобы доказать их справедливость также и для комплексных чисел, замените символы парами действительных чисел, примените формулы Гамильтона и убедитесь, что обе стороны дают одну и ту же пару. Проще простого. По иронии судьбы к тому моменту, когда Гаусс и Гамильтон разобрались во внутренней логике при помощи пар обычных «действительных» чисел, математики успели уже столько сделать с применением комплексных чисел, что практически потеряли интерес к приданию этим числам конкретного логического смысла.

Главными областями их применения были такие сферы физики, как магнитное и электрическое поля, гравитация и гидродинамика. Примечательно, что некоторые базовые уравнения комплексного анализа (дифференциальное и интегральное исчисление с комплексными функциями) точно соответствовали стандартным уравнениям математической физики. Поэтому теперь можно было решать уравнения физики при помощи дифференциального исчисления с комплексными числами. Главным ограничением было то, что комплексные числа лежат на плоскости. Поэтому физические процессы нужно было рассматривать как происходящие на плоскости или эквивалентные какой-то задаче на плоскости.

Комплексные числа придают плоскости систематическую алгебраическую структуру, которая превосходно приспособлена к геометрии, а следовательно, и к работе с движением. Оставшуюся часть этой главы можно рассматривать как двумерный предварительный разбор тех вопросов трехмерной геометрии, которым посвящена следующая глава. Там будет несколько формул – это алгебра, в конце концов, – но я не знаю, как этого избежать, ведь без них все выглядит как-то расплывчато.

Когда мы представляем комплексное число z в виде z = x + iy, где x и y действительные числа, в основе такого представления лежит геометрическая система декартовых координат с двумя осями, расположенными под прямым углом друг к другу: это действительная часть x (горизонтальная ось) и мнимая часть y (вертикальная ось). Однако на плоскости существует еще одна система координат – полярные координаты, в которых точка представляется как пара (r, A), где r – положительное действительное число, а A – угол. Эти две системы тесно взаимосвязаны: r – это расстояние от начала координат 0 до точки z, а A – угол между действительной осью и прямой, соединяющей начало координат с z.

Геометрия комплексной плоскости в декартовых и полярных координатах. Здесь cos и sin – тригонометрические функции косинус и синус. (Рисунок, по существу, определяет эти функции.)

Декартовы координаты идеальны для описания движения невращающихся объектов. Если точка x + iy смещается на a единиц по горизонтали и на b единиц по вертикали, она оказывается в точке (x + iy) + (a + ib). Если распространить эту идею на множество точек со списком значений для x и y, то все множество сдвинется на a единиц по горизонтали и на b единиц по вертикали в случае добавления фиксированного комплексного числа a + ib к каждой его точке. Более того, это жесткое движение: весь объект движется целиком, не меняя ни формы, ни размера.

Еще одним типом жесткого движения является вращение. Здесь объект опять же не меняет ни формы, ни размера, но изменяет ориентацию, поворачиваясь на некоторый угол вокруг центральной точки. Ключевое наблюдение здесь состоит в том, что умножение на i поворачивает точки на 90º вокруг центра в начале координат. Именно поэтому ось y, представляющая мнимую часть y числа z, расположена под прямым углом к оси x, которая представляет действительную часть x. (Несмотря на название, мнимая часть – это действительное число: она становится мнимой, когда мы умножаем ее на i, чтобы получить iy.)

Если мы хотим повернуть множество точек на 90°, то умножаем каждую точку этого множества на i. В более общем случае если мы хотим повернуть множество точек на угол A, то небольшое упражнение в тригонометрии покажет, что нужно умножить все точки множества на комплексное число

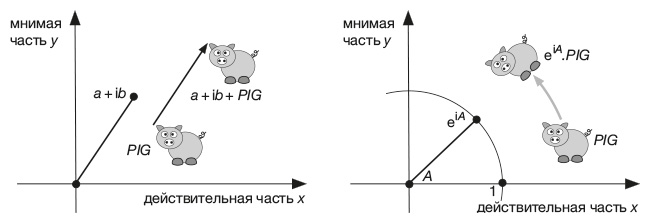
Параллельный перенос (слева) и поворот (справа) множества точек PIG с использованием комплексных чисел

Эйлер нашел замечательную и красивую связь между этим выражением и комплексным аналогом экспоненциальной функции e^x, где e = 2,71828… – основание натурального логарифма. Мы можем определить экспоненциальную функцию e^z комплексного числа z таким образом, чтобы она обладала теми же базовыми свойствами, что действительная экспонента, и совпадала с ней при действительном z. Оказывается, что

Элегантный способ понять, почему это происходит, состоит в использовании дифференциальных уравнений. Я поместил его в Примечания{50}, потому что выглядит все это слишком формально.

Представление комплексного числа в полярных координатах выглядит следующим образом:

Получилась очень простая и компактная формула.

Красота геометрии комплексных чисел заключается в том, что они имеют сразу две естественные координатные системы – декартову и полярную. Параллельный перенос в декартовых координатах описывается простой формулой, но в полярных координатах порождает путаницу. Поворот, напротив, в полярных координатах описывается простой формулой, зато в декартовых порождает путаницу. Пользуясь комплексными числами, вы можете сами выбирать, какое их представление лучше всего отвечает вашим целям.

Эти геометрические свойства комплексной алгебры можно было бы использовать в двумерной компьютерной графике, но оказывается, что, поскольку геометрия на плоскости проста, а компьютеры легко просчитывают громоздкие формулы, большой выгоды вы от этого не получите. В главе 7 мы увидим, что в случае компьютерной графики в трех измерениях аналогичный фокус творит чудеса. Однако пока мы завершим историю комплексных чисел рассказом о некоторых по-настоящему полезных сферах их применения.

Математики постепенно пришли к пониманию, что, несмотря на отсутствие очевидной физической интерпретации, комплексные числа часто оказываются проще, чем действительные, и проливают свет на такие свойства действительных чисел, которые в противном случае вызывают недоумение. Например, как заметили Кардано и Бомбелли, квадратные уравнения имеют либо два действительных корня, либо ни одного, а кубические уравнения – либо одно действительное решение, либо три. С комплексными решениями все намного проще: квадратные уравнения всегда имеют два комплексных решения, а кубические – всегда три. Можно, кстати говоря, продолжить: уравнения 10-й степени имеют 10 комплексных решений, а вот действительных решений у них может быть 10, 8, 6, 4, 2 или ни одного. В 1799 году Гаусс доказал давно подозреваемый факт, гипотезу о котором выдвинул Петр Рот еще в 1608 году и который получил известность как основная теорема алгебры: полиномиальное уравнение степени n имеет n комплексных корней. Все стандартные функции анализа, такие как экспонента, синус, косинус и т. п., имеют естественные комплексные аналоги, и при рассмотрении этих функций в комплексном варианте их свойства, как правило, становятся проще.

Одним из практических следствий этого стало превращение комплексных чисел в стандартные инструменты в электронике, в первую очередь потому, что они обеспечивают элегантный и простой способ работы с переменными токами. Электричество – это поток электронов, заряженных элементарных частиц. В постоянном токе, который дает, например, батарейка, электроны движутся в одном направлении. В переменном токе, который безопаснее и потому широко используется в электрических сетях, электроны снуют попеременно туда и сюда. График напряжения (и тока) в такой сети выглядит как кривая косинуса в тригонометрии.

Получить такую кривую можно, если последить за точкой на ободе вращающегося колеса. Предположим, для простоты, что радиус этого колеса равен 1. Если посмотреть на горизонтальную проекцию траектории нашей точки, то окажется, что она движется из стороны в сторону, достигая значений +1 и –1 в крайних положениях. Если колесо вращается с постоянной скоростью, то график горизонтального отклонения представляет собой кривую косинуса, а график вертикального отклонения – кривую синуса (кривые на рисунке, проведенные черными линиями).

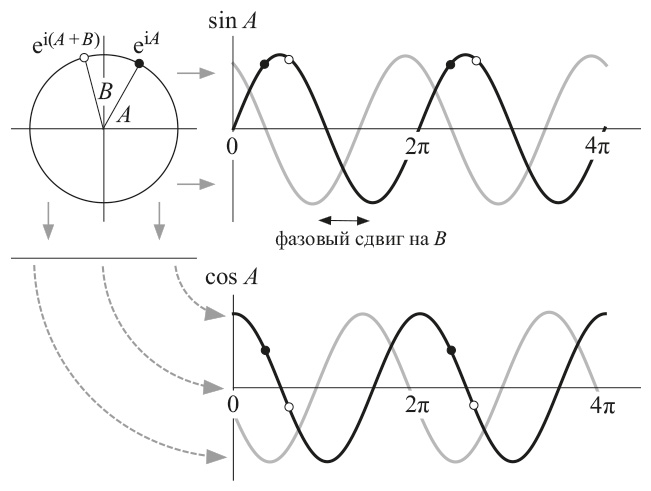
Вращение на комплексной плоскости в проекции дает периодические колебания. Прибавление B к углу A сдвигает графики влево: это так называемый фазовый сдвиг

Положение движущейся точки характеризуется парой действительных чисел (cos A, sin A), где A – угол между направлением на точку и горизонтальной осью. Воспользовавшись приемом Гамильтона, можно представить эту пару как комплексное число cos A + i sin A. С изменением угла A это число движется оборот за оборотом вдоль единичной окружности на комплексной плоскости. Если мы измеряем углы в радианах, то полный оборот точка совершает при увеличении A от 0 до 2π. Следующий оборот происходит, когда A возрастает от 2π до 4π, и т. д., так что движение точки носит периодический характер с периодом 2π.

Формула Эйлера подразумевает, что, по мере того как значение A, возрастая, проходит по действительным числам, соответствующее ему значение e^iA совершает оборот за оборотом вдоль единичной окружности с постоянной скоростью. Эта связь дает нам возможность превратить любое утверждение о периодической функции, имеющей форму синуса или косинуса, в комплексную экспоненту. Математически экспонента проще и легче поддается обработке. Более того, угол A имеет естественную физическую интерпретацию как фаза колебаний. Это означает, что изменение A путем прибавления к нему постоянного угла B сдвигает кривые синуса и косинуса на соответствующую величину (серые кривые на рисунке).

Что еще лучше, основные дифференциальные уравнения для напряжений и токов в контурах распространяются на множество комплексных чисел в неизменном виде. Физические колебания становятся действительной частью комплексной экспоненты, причем одни и те же методы применимы как к переменному, так и к постоянному току. Как будто вполне реальное (действительное) поведение имеет тайного мнимого двойника, и вместе они становятся проще, чем по отдельности. Инженеры-электронщики постоянно пользуются этим математическим приемом для упрощения расчетов, даже при наличии компьютера.

В электронике комплексные числа выскакивают как математический кролик из шляпы фокусника и облегчают инженерам жизнь – ну просто так получается. Но есть одна замечательная область, в контексте которой комплексные числа абсолютно необходимы и имеют физический смысл. Это квантовая механика.

Вигнер сделал этот образчик непостижимой эффективности центральным в своей лекции:

Кроме того, он постарался особо подчеркнуть, что подразумевается под «непостижимым»:

Квантовая механика возникла около 1900 года для объяснения странного поведения веществ в микромире, которое тогда вдруг начали обнаруживать физики-экспериментаторы, и очень быстро превратилась в самую успешную физическую теорию, когда-либо придуманную человечеством. Там – на уровне молекул, атомов и, особенно, элементарных частиц, из которых складываются атомы, – вещество ведет себя удивительно и загадочно. Настолько удивительно и загадочно, что совершенно неясно, применимо ли ко всему этому слово «вещество». Волны, такие как свет, иногда ведут себя как частицы, фотоны. Частицы, такие как электроны, иногда ведут себя как волны.

Эту двойственность волны-частицы (так называемый корпускулярно-волновой дуализм) со временем удалось описать с помощью математических уравнений, которые управляют одновременно волнами и частицами, хотя до сего дня многое остается загадкой. По ходу дела способ представления того и другого в математике пережил радикальную трансформацию и изменился до неузнаваемости. До того момента физики характеризовали состояние частицы вещества лишь небольшим набором параметров: масса, размер, положение в пространстве, скорость, электрический заряд и т. д. В квантовой механике состояние любой системы характеризуется волной, точнее говоря, ее волновой функцией. Как следует из названия, это математическая функция с волноподобными свойствами.

Функция – это математическое правило или процесс, который преобразует одно число в другое определенным образом. В более общем случае функция может преобразовывать список чисел в число или даже в другой список чисел. В еще более общем случае функция может оперировать не только числами, но и множеством математических объектов любого рода. Например, функция «площадь треугольника» действует для множества всех треугольников, и, когда вы применяете ее к конкретному треугольнику, значением функции становится площадь этого треугольника.

Волновая функция квантовой системы действует для списка возможных измерений, которые мы можем произвести в системе, таких как координаты ее положения и компоненты скорости. В классической механике состояние системы обычно определяется конечным числом таких чисел, но в квантовой механике список может включать бесконечно много переменных. Они берутся из так называемого гильбертова пространства, которое (часто) представляет собой пространство бесконечной размерности с однозначно определенным понятием расстояния между любыми двумя его точками{51}. Волновая функция дает на выходе единственное число для каждой функции в гильбертовом пространстве, но число это не действительное, а комплексное.

В классической механике наблюдаемое (величина, которую мы можем измерить) связывает каждое возможное состояние системы с числом. Например, если мы наблюдаем расстояние от Земли до Луны, то получаем в результате единственное число – наблюдаемое здесь есть функция, определенная на пространстве всех возможных конфигураций, в которых Земля и Луна могут хотя бы в принципе находиться. В квантовой механике наблюдаемые величины суть операторы. Оператор берет элемент гильбертова пространства состояний и превращает его в комплексное число. Операторы должны подчиняться короткому списку математических правил. Одно из них – линейность. Предположим, у вас есть два состояния x и y, и оператор L дает для них на выходе L(x) и L(y). В квантовой теории состояния могут накладываться друг на друга, наслаиваться – складываться – и давать в результате состояние x + y. Линейность означает, что оператор L должен в этом случае дать на выходе L(x) + L(y). Полный список требуемых свойств дает так называемый эрмитов оператор, который прекрасно ведет себя в связи с расстояниями в гильбертовом пространстве.

Физики выбирают эти пространства и операторы разными способами для моделирования конкретных квантовых систем. Если их интересуют состояния координат и импульса единичной частицы, гильбертово пространство состоит из всех квадратично интегрируемых функций и имеет бесконечную размерность. Если их интересует спин единичного электрона, гильбертово пространство двумерно и состоит из так называемых спиноров. В качестве примера можно привести уравнение Шрёдингера, которое выглядит примерно так:

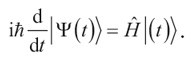
Вам не обязательно разбираться в математике, но давайте посмотрим на символы. Особенно на первый, который в значительной мере все проясняет: это i, квадратный корень из минус единицы. Мы смотрим на базовое уравнение квантовой механики, и первый же символ, который видим перед собой, – это мнимое число i.

Следующий символ, – это число, которое называют приведенной постоянной Планка, и оно очень-очень мало: около 10^–34 Дж∙сек. Именно оно дает квантовой механике ее кванты – крохотные, но дискретные скачки в значениях, которые могут принимать различные величины. Затем стоит дробь d/dt. Здесь t – время, а буквы d говорят нам о том, что следует найти скорость изменения, как в дифференциальном исчислении, так что это дифференциальное уравнение. Комбинация символов 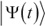– это волновая функция, определяющая состояние системы в момент времени t, то есть та штука, скорость изменения которой мы хотим узнать. Наконец, – это так называемый гамильтониан: по сути, энергия.

Обычная интерпретация волновой функции состоит в том, что она представляет не отдельное состояние, а вероятность того, что наблюдение обнаружит систему в этом состоянии. Однако вероятности – это действительные числа от 0 до 1, тогда как значения волновой функции – комплексные числа любой величины. Поэтому физики сосредоточиваются на амплитуде (которую математики называют модулем) комплексного числа, которая говорит о том, насколько далеко это число располагается от начала координат, – в полярных координатах это r. Они считают это число относительной вероятностью, так что если у одного состояния амплитуда равна 10, а у другого – 20, то второе состояние вдвое вероятнее первого.

Модуль говорит о том, насколько далеко от начала координат лежит комплексное число, но он ничего не говорит о направлении, в котором следует двигаться, чтобы до него добраться. Это направление определяется еще одним действительным числом, углом A в полярных координатах. Математики называют этот угол аргументом комплексного числа, а физики называют его фазой – насколько далеко вдоль единичной окружности следует пройти, чтобы выйти на нужное направление. Так что у комплексной волновой функции есть амплитуда, которая дает количественную оценку относительной вероятности данного наблюдения, и фаза, которая не влияет на амплитуду и которую почти невозможно измерить. Фазы влияют на то, как накладываются друг на друга отдельные состояния, и, следовательно, на вероятности возникновения этих составных состояний, но на практике они скрыты от взгляда экспериментатора.

Все это означает, что одного только действительного числа недостаточно для количественного определения квантового состояния. Невозможно даже сформулировать квантовую механику с помощью традиционных действительных чисел.

Если вопрос в том, какие практические применения имеют комплексные числа, то можно указать на квантовую механику в полной уверенности, что они непременно находят применение там. До недавнего времени в большинстве случаев это относилось к лабораторным экспериментам – самому что ни на есть переднему краю физики, но не к тому, что можно обнаружить на собственной кухне или в гостиной. Современная электроника полностью изменила ситуацию, и многие из наших любимых устройств работают по квантово-механическим причинам. Их конструкторы должны разбираться в подобных вещах очень глубоко, а мы можем просто сидеть в сторонке и восхищаться их творениями. Или время от времени ругать их, когда они не делают того, что нам нужно, из-за непонятных технических заморочек с конфигурированием этой проклятой штуковины.

В данном случае я имею в виду свою новенькую оптоволоконную широкополосную линию связи. Выглядит она как обычный кабель, но является частью передающей системы, которая уже опирается на квантовые технологии. Впрочем, ее квантовая часть заключается не в кабеле как таковом: она в устройствах на маршруте, генерирующих световые импульсы, на которых построена работа всей сети. Конечно, свет в любом случае имеет квантовый характер, но эти устройства сконструированы с использованием квантовой механики и не могли бы работать без нее.

Слово «волоконный» в названии означает многожильный кабель, где отдельные волокна представляют собой тонкие стеклянные нити, по которым передается свет. Они сделаны так, что свет отражается от их стенок и не выходит наружу, поэтому такие кабели можно изгибать – свет все равно остается внутри. Информация в световом луче кодируется в виде серии коротких импульсов. Оптическое волокно начали использовать в телекоммуникационной отрасли, потому что оно имеет ряд преимуществ. Современное волокно обладает высокой прозрачностью и потому передает свет на большие расстояния без ослабления сигнала. Световые импульсы способны нести намного больше информации, чем можно передать по традиционному медному телефонному проводу. Именно большая ширина полосы пропускания обеспечивает повышенную «скорость» – дело не столько в том, с какой скоростью движутся импульсы, сколько в числе этих самых импульсов – и, соответственно, в количестве информации, – которое можно втиснуть в одно волокно или в один кабель. Оптоволоконные кабели легче медных, поэтому их проще перевозить и монтировать, и меньше подвержены влиянию электрических помех.

Оптические системы связи включают в себя четыре основных компонента: передатчик (источник света); кабель для передачи сигнала; ряд повторителей, которые подхватывают сигнал, пока он не слишком сильно ослаб, очищают его и ретранслируют; и, конечно, приемник (детектор). Я сосредоточу свое внимание только на одном из этих компонентов – на передатчике. Это должно быть устройство, способное генерировать серии световых импульсов, которые можно включать (1) и выключать (0), чтобы эта серия представляла собой сообщение в двоичном коде. Включение/выключение должно происходить чрезвычайно быстро и с очень высокой точностью. В частности, длина волны («цвет») света должна иметь одно значение. Наконец, импульсы должны сохранять свою форму, чтобы приемник мог их распознать.

Идеальным (и, строго говоря, единственным) гаджетом, способным это делать, является лазер – устройство, испускающее мощный луч когерентного света с определенной длиной волны. Когерентность означает, что все волны в луче находятся в одной фазе и потому не подавляют друг друга. Чтобы добиться этого, лазер гоняет свет (в виде фотонов) туда и обратно между двумя зеркалами, инициируя при этом благодаря положительной обратной связи все более мощный каскад фотонов. Когда луч становится достаточно мощным, его выпускают.

Первые лазеры были большими и неудобными, но сегодня при создании большинства легких лазеров используются примерно те же процессы, что и при производстве микроскопических цепей в компьютерных чипах – интегральных полупроводниковых схемах. Последние 30 лет почти все лазеры, используемые в бытовых и промышленных устройствах (таких как плееры Blu-Ray, которые стали возможны после изобретения лазеров, дающих синий свет), представляют собой гетероструктурные лазеры с раздельным удержанием (SCH). Это улучшенная разновидность лазера на квантовых ямах, которые похожи на сэндвич, средний слой которого работает как квантовая яма. Такая структура создает волновые функции, похожие скорее на серию ступенек, чем на кривую, так что энергетические уровни в них оказываются квантованными – они резко отличаются друг от друга, а не сливаются размытыми пятнами. Эти уровни можно настроить при помощи подходящей конструкции квантовой ямы, чтобы получить свет нужной частоты для работы лазера.

В SCH-лазерах сверху и снизу сэндвича добавляют еще два слоя с более низким коэффициентом преломления, чем у трех средних слоев, и эти два слоя запирают свет внутри резонатора лазера. Нетрудно предположить, что сконструировать квантовое устройство такого типа невозможно без активного применения квантовой механики. Так что даже в волоконной оптике 1990-х годов использовались квантовые компоненты, а на сегодняшний день это утверждение стало еще более верным.

В будущем появится громадное разнообразие новых квантовых устройств, которые преобразят нашу жизнь. Принцип неопределенности Гейзенберга для квантовой механики гласит, что определенные наблюдаемые параметры невозможно точно измерить в одно и то же время – например, если вы знаете, где в точности находится частица, то не можете с уверенностью сказать, как быстро она движется. Это свойство позволяет определять, не слушает ли секретные сообщения кто-нибудь, не имеющий такого права. Когда Ева (устройство перехвата сообщений) потихоньку наблюдает за квантовым состоянием проходящего сигнала – скажем, за спином фотона, – то состояние изменяется и она не может контролировать характер этого изменения. Как будто в сообщение встроен колокольчик, который звонит всякий раз, когда Ева пытается это сообщение прочесть.

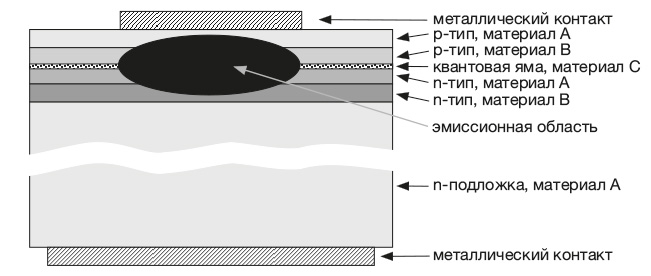
Схематичное изображение структуры SCH-лазера. Термины n-тип и p-тип относятся, соответственно, к полупроводникам, где заряд переносится электронами или «дырками»

Один из способов реализации этой идеи состоит в использовании квантовой фотоники – квантово-механических свойств фотонов. Другой способ – манипулирование спинами квантовых частиц, этим занимается развивающаяся область – спинтроника. Подобные устройства могут переносить больше информации, чем традиционный сигнал, за счет кодирования дополнительных данных в спинах частиц, а не только в их присутствии или отсутствии. Так что моя сверхбыстрая оптоволоконная широкополосная связь, вполне возможно, скоро превратится в супер-пупер-быструю спинтронную широкополосную связь, способную по тому же кабелю передать гораздо больше информации. И она будет действовать, пока какой-нибудь умник не изобретет шестимерную гиперчеткую сенсорную голографию и не перекроет разом всю эту дополнительную пропускную способность.