Это база: Зачем нужна математика в повседневной жизни

11 Мы уже почти приехали?

Этот сценарий знаком каждому родителю, который водит машину. Семья направляется в другой город навестить бабушку, до нее 400 с лишним километров и шесть часов езды. Дети разместились на заднем сиденье. Через полчаса после отправления сзади начинают ныть: «Мы уже почти приехали?»

Здесь у меня имеются разногласия с заокеанскими родичами, которые, похоже, убеждены, что фраза звучит немного иначе: «Мы уже приехали?» Может быть, в США спрашивают именно так, но это неверно, потому что такой вариант говорит о недопонимании. Ответ в этом случае всегда очевиден: мы либо приехали и тогда вопрос излишен, либо нет и тогда спрашивать бесполезно. Нет, на самом деле в любом долгом путешествии, когда дети начинают капризничать, добрые (или просто раздраженные) родители их успокаивают: «Уже почти приехали». Даже если до места добираться еще пять часов. На некоторое время это успокаивает детей. В любом случае после нескольких поездок дети начинают адресовать родителям этот вопрос скорее с отчаянием, чем с надеждой: «Мы уже почти приехали?» Это разумный вопрос, потому что определить местоположение, глядя в окно, невозможно. Если, конечно, вы не знаете местных ориентиров. У нас когда-то был кот, который их знал.

Мы уже почти приехали? Где мы сейчас? Два десятилетия назад для ответа на этот вопрос нужна была карта, хорошие навыки ее чтения и штурман на пассажирском сиденье. Сегодня эти задачи отданы на откуп всевозможным электронным помощникам. Вам достаточно посмотреть на прибор спутниковой навигации. Правда, он иногда заводит людей в чистое поле, где и бросает. Одна машина не так давно заехала по указаниям навигатора в реку. Так что на дорогу смотреть тоже полезно. Но даже эта предосторожность может не помочь. В прошлом году мы, занимаясь поисками придорожного мотеля, заехали во двор сельского дома, потому что наш спутниковый навигатор не смог отличить настоящую дорогу, похожую на подъездную дорогу к усадьбе, от подъездной дороги к усадьбе, похожей на настоящую дорогу.

Спутниковая навигация похожа на волшебство. У вас в машине есть экран, на котором видна часть карты. Эта карта показывает в точности, где вы находитесь. Вы едете вперед, и карта движется так, что символ, обозначающий вашу машину, всегда находится в правильном месте. Устройство знает, в каком направлении вы едете, ему известно название или номер дороги, на которой вы находитесь. Оно предупреждает вас о пробках. Оно знает, куда вы едете и как быстро, когда превышаете скорость, где находятся дорожные камеры и скоро ли вы окажетесь у ближайшей из них. Научите детей пользоваться этой информацией, и они перестанут спрашивать.

«Любая достаточно развитая технология, – писал великий фантаст и футуролог Артур Кларк, – неотличима от магии». Другой писатель-фантаст Грегори Бенфорд переиначил Кларка так: «Любая технология, которую можно отличить от магии, развита недостаточно». Спутниковая навигация достаточно развита, но не является магией. Как она работает?

Прибор знает, куда вы едете, потому что вы сами ему об этом сказали. Для этого вы прикасались к буквам и цифрам на экране. Это очевидно. Кстати говоря, очевидно здесь только это. Остальное опирается на высокие технологии – спутники на орбитах, радиосигналы, коды, псевдослучайные числа и много-много хитроумных компьютерных вычислений. Алгоритмы для поиска самого быстрого/дешевого/безопасного для окружающей среды маршрута. Совершенно необходима теоретическая физика: орбитальная механика, основанная на законе всемирного тяготения Ньютона, дополненном специальной теорией относительности Эйнштейна и его же общей теорией относительности. Спутники на орбитах передают так называемый дальномерный код – сигналы с точной временно́й привязкой. У вас же почти все происходит в одном крохотном компьютерном чипе. Плюс задействуются какие-то чипы памяти, где хранятся карты и т. п.

Мы ничего этого не видим и воспринимаем как магию.

Стоит ли говорить, что значительная часть магии носит математический характер и требует немалых объемов математики из множества областей, а также физики, химии, материаловедения и инженерных премудростей. Возможно, некоторым пользователям не помешала бы и психиатрическая помощь, ну да ладно.

Даже если оставить в стороне производство и создание космических аппаратов и технологий их доставки на орбиту, в спутниковой навигации задействовано не менее семи областей математики, без которых она работать не будет. Вот что я имею в виду:

• Расчет траекторий ракет-носителей, доставляющих спутники на орбиту.

• Баллистическое проектирование набора орбит, позволяющего получить хорошее покрытие территории: необходимо, чтобы из любой точки в любой момент были видны по крайней мере три спутника, но лучше больше.

• Использование генератора псевдослучайных чисел для создания сигналов, позволяющих измерять с высокой точностью расстояние до каждого из спутников.

• Использование тригонометрии и орбитальных данных для вычисления положения вашей машины.

• Использование уравнений специальной теории относительности для внесения в расчеты поправок, связанных с действием высокой скорости движения спутников на ход времени.

• Использование уравнений общей теории относительности для внесения в расчеты поправок, связанных с действием гравитации Земли на ход времени.

• Решение одного из вариантов задачи коммивояжера для нахождения лучшего маршрута в соответствии с выбранным вами критерием: самого быстрого, самого короткого, наименее вредного для окружающей среды.

О большей части перечисленного я расскажу подробнее на следующих страницах, причем больше всего внимания постараюсь уделить самым удивительным моментам.

Спутниковая навигация зависит от чрезвычайно точных синхронизированных сигналов, получаемых при помощи атомных часов и рассылаемых со специальных орбитальных аппаратов. Цезиевые часы сами по себе очень точны и имеют погрешность хода не более чем 5/10¹⁴, то есть ошибаются не более чем на 4 наносекунды в сутки. Это соответствует ошибке в определении вашего положения, равной примерно одному метру в сутки. Чтобы скомпенсировать постепенный дрейф, часы периодически синхронизируются с наземной станцией. Существуют и другие источники временны́х ошибок, к которым я еще вернусь.

В настоящее время существует несколько спутниковых навигационных систем, но я сосредоточусь на первой и наиболее широко используемой из них – Global Positioning System (GPS). Проект был начат в 1973 году под эгидой Министерства обороны США. Основа системы – группировка орбитальных аппаратов: первоначально их было 24, теперь 31. Первый спутник-прототип был запущен в 1978 году, а полная группировка начала функционировать в 1993 году. Первоначально система GPS предназначалась для военного использования, но указ президента Рональда Рейгана от 1983 года сделал ее доступной гражданам в низком разрешении. GPS постоянно модернизируется, и еще несколько стран в настоящее время имеют собственные системы спутникового позиционирования, начиная с российской Глобальной навигационной спутниковой системы (ГЛОНАСС), дающей точность до двух метров. В 2018 году Китай начал создавать свою навигационную спутниковую систему BeiDou, которая сейчас, возможно, функционирует в полном объеме. Навигационная система Европейского союза называется Galileo. Великобритания покинула ЕС и не участвует теперь в эксплуатации системы, но в ознаменование триумфа идеологии над здравым смыслом объявила о разработке собственной системы навигации. Индия строит NavIC, а Япония – Quasi-Zenith Satellite System (QZSS), что должно позволить им ликвидировать зависимость от GPS к 2023 году.

Первоначальная группировка GPS из 24 спутников, по четыре на каждой из шести орбит[10]

С технической точки зрения GPS включает в себя три «сегмента»: космический (собственно спутники), управляющий (наземные станции) и пользовательский (вы в своей машине). Спутники рассылают дальномерные коды. Управляющий сегмент следит за орбитами спутников и точностью их часов и при необходимости передает команды на коррекцию орбиты или синхронизацию часов. Пользователю достаточно дешевого маломощного приемника, встроенного в мобильный телефон и сообщающего приложениям, где он находится.

Совокупность спутников традиционно называется «группировкой». По проекту группировка GPS включает в себя 24 спутника на примерно круговых орбитах на высоте 20 200 км над поверхностью Земли, или 26 600 км от ее центра. Я оставлю в стороне более поздние дополнительные спутники, которые не меняют основную идею, а лишь делают систему более надежной и точной. Существует шесть орбит в плоскостях, пересекающих плоскость экватора под углом 55° и распределенных равномерно вдоль экватора. На каждой орбите находятся четыре равноудаленных спутника, которые вечно гонятся друг за другом. Радиус орбиты рассчитан таким образом, чтобы спутник возвращался в одну и ту же точку орбиты каждые 11 часов 58 минут. В результате он оказывается примерно над одним и тем же местом на Земле дважды в сутки, но при этом медленно дрейфует.

Следующий математический элемент – геометрия орбиты. Такая конфигурация орбит и размещения спутников означает, что в любой момент по крайней мере шесть спутников видны (то есть сигналы с них могут быть получены) из любой точки планеты. Какие именно шесть, зависит от того, где вы находитесь, и этот набор меняется со временем, поскольку Земля вращается и спутники тоже обращаются по своим орбитам.

В системе GPS пользователям не нужно передавать на спутники никакой информации. У них есть приемник, который принимает дальномерные коды со всех видимых на данный момент спутников. Приемник обрабатывает сигналы с точной привязкой ко времени, чтобы определить с их помощью, где он находится. Базовый принцип прост, так что давайте сначала рассмотрим его. Затем я укажу на некоторые тонкости, о которых необходимо позаботиться, чтобы эта система работала в реальном мире.

Начнем с одного спутника. Он отправляет дальномерные коды, по которым ваш приемник определяет, как далеко этот спутник находится в настоящий момент. (Позже мы увидим, как это рассчитывается.) Возможно, это расстояние составляет 21 000 км. Если исходить из этой информации, то вы находитесь на поверхности сферы со спутником в центре и радиусом 21 000 км. Сама по себе такая информация не слишком полезна, но в это же мгновение видимы еще по крайней мере пять спутников. Я буду называть их спутником 2, спутником 3 и т. д. до спутника 6. Каждый из них передает свои сигналы, которые вы принимаете одновременно, и каждый сигнал помещает вас на свою сферу с соответствующим спутником в центре: это сферы 2, 3, 4, 5, 6. Сигнал со спутника 2 совместно с сигналом со спутника 1 помещает вас на пересечение сфер 1 и 2, которое представляет собой окружность. Спутник 3 добавляет в эту систему свою сферу, которая пересекается со сферой 1 по другой окружности. Эти две окружности пересекаются друг с другом в двух точках, каждая из которых лежит на всех трех сферах. Сигнал от спутника 4 образует сферу 4, которая в общем случае позволяет определить, какая из двух точек является вашим истинным местоположением.

В идеальном мире мы могли бы остановиться на этом, и привлечение спутников 5 и 6 было бы уже излишне. В реальности все не так просто. Всюду могут возникать ошибки. Атмосфера Земли может исказить сигнал, его прохождению могут помешать радиопомехи или еще что-нибудь. Для начала из этого следует, что ваше местоположение скорее близко к соответствующей сфере, а не на ней. Точка вашего местоположения лежит не на поверхности сферы, а скорее в пределах утолщенной оболочки, включающей в себя эту поверхность. Так что четыре спутника и их четыре сигнала могут определить ваше положение с некоторым уровнем точности, но не идеально. Чтобы улучшить результат, GPS использует дополнительные спутники. Их утолщенные сферические оболочки еще сильнее сужают область вашего возможного пребывания. На этом этапе уравнения, определяющие ваше положение, почти наверняка несовместимы друг с другом, если не обращать внимания на вероятные ошибки, но, воспользовавшись старым статистическим приемом, можно минимизировать суммарную ошибку и получить наилучшую оценку положения. Этот прием, известный как метод наименьших квадратов, был предложен Гауссом в 1795 году.

В результате вашему GPS-приемнику достаточно систематически производить серию относительно простых геометрических расчетов, которая и приведет к наилучшей возможной для этого прибора оценке местоположения. Сравнивая полученный результат с детализированной формой Земли, прибор может определить даже, как высоко над уровнем моря вы находитесь. Как правило, высоты определяются менее точно, чем координаты по широте/долготе.

Спутник «рассылает дальномерные коды», или, говоря иначе, «рассылает сигналы с точной привязкой по времени». Звучит просто, но на самом деле это не так. Если вы слышите раскат грома, то понимаете, что начинается гроза, но сам по себе раскат грома не скажет вам, насколько она далека. Если же вы не только слышите гром, но и видите молнию, что происходит раньше, чем раздается гром, поскольку свет распространяется быстрее звука, то можно использовать разницу во времени прихода двух сигналов для оценки расстояния до молнии. Для прикидки достаточно знать, что три секунды запаздывания соответствуют примерно одному километру. Однако скорость звука зависит от состояния атмосферы, так что это правило нельзя считать точным.

GPS не может использовать в качестве второго сигнала звуковые волны по очевидным причинам – они слишком медленные, к тому же в космосе царит вакуум, так что звук там в любом случае не может распространяться. Но сама идея получения временно́й разницы между двумя разными, но взаимосвязанными сигналами верная. Каждый спутник рассылает последовательность импульсов 0/1, не содержащую повторений, – разве что вы будете ждать очень долго, чтобы последовательность повторилась целиком. GPS-приемник может сравнить строку из нулей и единиц, которую он получает со спутника, с той же строкой, получаемой от местного источника. Спутниковый сигнал приходит с задержкой, потому что ему приходится преодолевать расстояние между спутником и приемником, а время задержки можно определить, выровняв оба сигнала и посмотрев, насколько нужно сдвинуть один из них, чтобы он соответствовал второму.

Мы можем проиллюстрировать этот процесс, используя вместо нулей и единиц слова из этой книги.

Предположим, что сигнал, полученный со спутника, таков:

тогда как опорный сигнал, получаемый одновременно практически с соседнего двора, таков:

Тогда мы можем сдвинуть местный сигнал так, чтобы одинаковые слова совпали, примерно так:

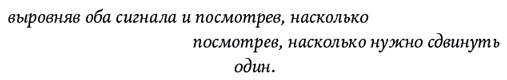
Теперь мы видим, что сигнал со спутника приходит на четыре слова позже местного сигнала.

Остается только сгенерировать подходящие битовые строки. Простой способ генерирования строки из нулей и единиц с очень редкими повторениями состоит в подбрасывании монеты миллионы раз с записью 0 для орла и 1 для решки. Каждый бит возникает с вероятностью 1/2, так что строка из, скажем, 50 бит возникает с вероятностью 1/2⁵⁰, что соответствует примерно одному шансу на квадриллион. В среднем она повторится примерно через квадриллион знаков вдоль строки. Если сравнить такой сигнал с его вариантом, смещенным на гораздо меньшую величину, то «верное» смещение, дающее наилучшее совпадение строк, окажется единственным.

Компьютеры, однако, не сильны в подбрасывании монет. Они следуют конкретным инструкциям, и весь смысл их работы состоит в том, что они должны делать это точно и безошибочно. К счастью, существуют точные математические процессы, способные генерировать битовые строки, которые кажутся случайными в разумном статистическом смысле, хотя реальная процедура их создания носит детерминистский характер. Подобные методы известны как генераторы псевдослучайных чисел. Это третий крупный математический ингредиент системы GPS.

На практике поток битов из генератора псевдослучайных чисел объединяется с другими данными, которых требует GPS, – такой метод называется модуляцией. Спутник передает данные с относительно невысокой скоростью: 50 бит в секунду. Он соединяет этот сигнал с куда более быстрым потоком битов из генератора псевдослучайных чисел, скорость которого более миллиона чипов в секунду. Чип здесь – примерно то же, что и бит, но значения он принимает +1 или –1, а не 0 или 1. Физически это прямоугольный импульс с амплитудой либо +1, либо –1. «Модуляция» означает, что первоначальная строка данных умножается на значение чипа в каждое мгновение. Поскольку все другие данные меняются, по сравнению с этим, очень медленно, методика «сдвинуть и совместить» по-прежнему работает достаточно хорошо, но иногда сигналы совпадают полностью, а иногда они оказываются противоположными по знаку. Если воспользоваться статистическим методом корреляции, то получится, что вам нужно просто сдвигать сигналы друг относительно друга, пока их корреляция не станет достаточно высокой.

Мало того, GPS проделывает то же самое и с другим псевдослучайным числом, модулирующим сигнал на вдесятеро большей скорости. Более медленный сигнал называется «код грубого определения местоположения объектов» и предназначен для гражданского использования. Более быстрый – «точный код» – зарезервирован для военных. Он, кроме того, зашифрован и повторяется не чаще чем раз в семь суток.

Генераторы псевдослучайных чисел, как правило, основаны на абстрактной алгебре, такой как многочлены над конечными полями, или на теории чисел, такой как целые числа по некоторому модулю. Простой пример последнего – линейный конгруэнтный генератор. Выберем модуль m, два числа a и b (mod m) и начальное число x₁ (mod m). Затем определим последовательные числа x₂, x₃, x₄ и т. д., вычисляемые по формуле

где a играет роль постоянного множителя текущего числа x_n, а b сдвигает полученное значение на постоянную величину. Это дает следующее число последовательности, после чего операция повторяется. Например, если m = 17, a = 3, b = 5 и x₁ = 1, то мы получаем последовательность

которая затем повторяется бесконечно. Никаких явных закономерностей, заметных глазу, здесь нет. На практике, разумеется, m намного больше. Существуют математические условия, которые гарантируют, что последовательность повторяется очень и очень редко и при этом удовлетворяет разумным статистическим тестам на случайность. Например, после превращения выходной последовательности в двоичную, каждое число (по модулю m) должно появляться в ней с равной частотой в среднем. То же можно сказать и о каждой строке из нулей и единиц заданной длины, вплоть до некоторого разумного размера.

Линейные конгруэнтные генераторы слишком просты, чтобы быть надежными, поэтому были разработаны более сложные варианты. В качестве примера можно назвать вихрь Мерсенна, который придумал Макото Мацумото в 1997 году. Такой генератор наверняка есть у многих из вас, потому что он используется в десятках стандартных программных пакетов, в том числе в Microsoft Excel. В вихре Мерсенна сочетаются простые числа, благодаря которым математика упрощается, и симпатичные двоичные выражения, упрощающие вычисления. Простое число Мерсенна – это число вида 2^p – 1 (где p – простое число), такое как 31 = 2⁵–1 или 131 071 = 2¹⁷–1. Простые числа Мерсенна встречаются редко, и мы даже не знаем, бесконечно ли их количество. В январе 2021 года было известно ровно 51 простое число Мерсенна, самое большое из которых равно 2^{82 589 933}–1.

В двоичном виде два простых числа Мерсенна выглядят так:

и представляют собой 5 и 17 единиц соответственно. Это позволяет цифровому компьютеру легко оперировать ими при вычислениях. Вихрь Мерсенна основан на каком-нибудь очень большом простом числе Мерсенна, обычно 2^{19 937}–1, и он заменяет числа в сравнениях матрицами над полем с элементами 0 и 1. Этот метод удовлетворяет тестам для подстрок длиной вплоть до 623 бит.

Сигнал GPS включает в себя также сигнал гораздо более низкой частоты, несущий информацию об орбите спутника, его временны́х поправках и других факторах, влияющих на статус системы. Возможно, это кажется сложным – так оно и есть на самом деле, – но современная электроника способна безошибочно выполнять чрезвычайно сложные инструкции. Для такой сложности существуют серьезные причины. Она помогает приемнику не захватить случайно какой-то другой сигнал, поскольку крайне маловероятно, что он воспроизведет такую сложную закономерность. Каждому спутнику присваивается собственный псевдослучайный код, и та же сложность гарантирует, что приемник не спутает сигнал одного спутника с сигналом другого. Помимо прочего, все спутники могут работать на одной и той же частоте, не глуша друг друга, что позволяет высвободить дополнительные частоты в нашем все более забитом радиодиапазоне. К тому же, что особенно важно для военных, противник не может вмешаться в работу системы или организовать передачу ложных сигналов. В целом псевдослучайным кодом распоряжается Министерство обороны США, так что оно может контролировать доступ к GPS.

Помимо постепенного дрейфа атомных часов, существуют и другие источники временны́х погрешностей, например небольшие отклонения формы и размера орбит спутников от расчетных. Наземная станция передает связанные с этим поправки на спутник, который в свою очередь раздает их пользователям, обеспечивая синхронность с эталонными часами Военно-морской обсерватории США. Однако наибольшую погрешность вносят релятивистские эффекты, так что вместо доброй старой ньютоновской физики нам здесь не обойтись без эйнштейновских теорий относительности{61}.

В 1905 году Эйнштейн опубликовал статью «К электродинамике движущихся тел». Он исследовал связь между ньютоновской механикой и максвелловскими уравнениями электромагнетизма и нашел две эти теории несовместимыми друг с другом. Главной проблемой здесь является то, что скорость, с которой распространяются электромагнитные волны, – скорость света – постоянна не только в неподвижной системе координат, но и в движущейся системе. Если посветить фонариком с мчащегося автомобиля, фотоны будут лететь в пространстве с той же скоростью, что и испускаемые из неподвижного автомобиля.

В ньютоновской физике скорость автомобиля следовало бы прибавить к скорости света. Эйнштейн предлагал модифицировать ньютоновские законы движения таким образом, чтобы скорость света в них была абсолютной константой. Это означало, что и уравнения для относительного движения тоже следовало модифицировать. По этой причине новая идея получила название теории относительности. Это может вводить в заблуждение, поскольку ее основная мысль состоит как раз в том, что скорость света не относительна. Много лет Эйнштейн пытался включить в свою теорию и гравитацию, что ему в конечном итоге удалось сделать в 1915 году. Эти две родственные, но отдельные теории получили известность как специальная и общая теории относительности соответственно.

Настоящая книга не учебник по теории относительности, поэтому я лишь слегка коснусь некоторых основных моментов, чтобы дать вам очень упрощенную картину того, о чем идет речь. Мы не будем вдаваться в философские нюансы, которые далеки от нашей темы.

В специальной теории относительности уравнения движения модифицированы таким образом, чтобы скорость света имела одинаковое значение в любой системе координат, движущейся с постоянной скоростью. Достигается это при помощи преобразований Лоренца – математических формул, названных в честь нидерландского физика Хендрика Лоренца и описывающих, как меняются координаты и время при сравнении разных систем отсчета. Основные предсказания этой теории с ньютоновской точки зрения выглядят очень странно. Ничто не может двигаться быстрее света; длина объекта уменьшается с увеличением скорости и становится сколь угодно малой по мере того, как скорость приближается к скорости света; при этом субъективное время замедляется до черепашьей скорости, а масса неограниченно растет. Грубо говоря, при скорости света длина объекта (в направлении движения) уменьшается до нуля, время останавливается, а масса становится бесконечной.

Общая теория относительности сохраняет все эти элементы, но встраивает в систему еще и гравитацию. Однако гравитация здесь уже не сила, как представлял ее Ньютон, а эффект кривизны пространства-времени – четырехмерного математического конструкта, объединяющего три пространственных измерения и одно временно́е. Вблизи любой массы, например массы звезды, пространство-время искривляется, образуя своеобразную вмятину, но в четырех измерениях. Световой луч или частица, пролетающие мимо, отклоняются от прямой траектории и следуют за кривизной. Это создает иллюзию притягивающей силы, действующей между звездой и частицей.

Обе теории получили основательное подтверждение при помощи высокочувствительных экспериментов. Несмотря на свою необычность, они дают наилучшую модель реальности, известную физикам. Математика GPS должна учитывать релятивистские эффекты, обусловленные как скоростью спутника, так и гравитационной ямой Земли, – в противном случае система GPS будет бесполезной. В самом деле, успех GPS со всеми этими поправками – серьезный тест на истинность как специальной, так и общей теории относительности.

Большинство пользователей GPS либо неподвижны относительно поверхности Земли, либо движутся медленно – чаще всего не быстрее автомобиля. По этой причине конструкторы решили передавать информацию об орбитах спутников с использованием системы отсчета, жестко привязанной к вращающейся Земле, и считать, что скорость ее вращения постоянна. Форма нашей планеты, называемая геоидом, приблизительно соответствует слегка уплощенному эллипсоиду вращения.

Когда вы находитесь в машине, а спутники проносятся где-то в вышине, они, очевидно, движутся относительно вас. Специальная теория относительности говорит, что для вас часы на спутнике будут тикать медленнее, чем эталонные часы на Земле. Они должны отставать примерно на 7 микросекунд в сутки из-за релятивистского растяжения времени. Помимо этого, сила тяготения на высоте спутниковых орбит очевидно меньше, чем на поверхности Земли. С точки зрения общей теории относительности пространство-время наверху, рядом со спутниками, является более плоским – менее искривленным, – чем возле вашего автомобиля. Этот эффект заставляет часы на спутнике идти быстрее наземных часов. Общая теория относительности предсказывает, что они должны обгонять наземные часы на 45 микросекунд в сутки. Сложив эти разнонаправленные эффекты, мы получим, что часы на спутнике должны идти быстрее часов на Земле примерно на 45–7 = 38 микросекунд в сутки. Такая ошибка стала бы заметной через две минуты, а ваше местоположение смещалось бы на 10 км в сутки от правильной точки. Всего за сутки спутниковый навигатор переместил бы вас в другой город, за неделю – в другую область, за месяц – в другую страну.

Первоначально инженеры и ученые, работавшие над проектом GPS, не были уверены в том, что релятивистские эффекты имеют значение. Спутники, конечно, летят быстро по нашим меркам, но по сравнению со скоростью света они лишь медленно ползут. Тяготение Земли в космических масштабах тоже очень невелико. Так или иначе, величины этих эффектов постарались оценить как можно точнее. В 1977 году, когда на орбиту был выведен первый прототип цезиевых атомных часов (или атомного стандарта частоты, как это чаще называют), разработчики все еще не могли точно сказать, насколько велики эти эффекты и будут ли они положительными или отрицательными. Некоторые вообще считали, что релятивистские поправки не потребуются. Так что инженеры включили в часы схему, способную по сигналу с Земли изменять их частоту, чтобы скомпенсировать предсказанные релятивистские эффекты при необходимости. В первые три недели они, не включая эту схему, тщательно измеряли частоту часов, которая оказалась на 442,5 триллионных долей выше частоты наземного эталона. Общая теория относительности предсказывала повышение частоты на 446,5 триллионных долей. Весьма точное попадание.

GPS используется для решения множества других задач, помимо очевидного позиционирования (машин, коммерческого транспорта, туристов) и военных применений, которые, собственно, и привели в свое время к созданию этой глобальной системы. Я упомяну лишь несколько таких задач.

Вам не обязательно знать, где вы находитесь, при вызове через специальную программу службы техпомощи при поломке машины – GPS сделает все сама. Кроме того, система используется для предотвращения угона автомобилей, для картографирования и геодезических измерений, для отслеживания перемещений домашних животных и пожилых родственников, а также для охраны произведений искусства. Среди главных областей применения – морская и воздушная навигация и отслеживание движения судов для транспортных компаний. Теперь, когда в большинстве сотовых телефонов имеются GPS-приемники, вы можете привязывать фотографии к месту, где они сделаны, GPS поможет определить местоположение потерянного или украденного телефона и вызвать такси. GPS в сочетании с интерактивными картами, такими как Google Maps, автоматически показывает, где вы находитесь. Фермерам она позволяет управлять беспилотными тракторами, банкирам – мониторить финансовые переводы, туристам – отслеживать свой багаж. Ученые с помощью GPS могут наблюдать за миграцией редких видов животных и отслеживать последствия экологических катастроф, таких как разливы нефти.

Как же мы прежде обходились без GPS? Поразительно, насколько быстро математическая магия, открывающая простор для революционных (и очень дорогостоящих) технологий, может изменить нашу жизнь.