Это база: Зачем нужна математика в повседневной жизни

5 Будьте осторожны в киберпространстве

Пьер де Ферма знаменит своей Великой теоремой, которая гласит, что если n равно по крайней мере 3, то сумма двух n-х степеней целых чисел не может также быть n-й степенью целого числа. Эндрю Уайлс в конечном итоге нашел этому современное формальное доказательство в 1995 году, примерно 358 лет спустя после того, как Ферма высказал свою гипотезу{39}. По профессии Ферма был юристом, советником парламента в Тулузе, но большую часть времени посвящал математике. У него был друг по имени Френикль де Бесси, парижский математик, известный прежде всего полным каталогом 880 магических квадратов четвертого порядка. Они активно переписывались, и 18 октября 1640 года Ферма написал де Бесси (по-французски), что «каждое простое число делит… одну из степеней любой прогрессии за вычетом единицы, а показатель этой степени делит данное простое число за вычетом единицы».

Если перевести этот текст на алгебраический язык, то Ферма утверждал, что если p – простое число и a – произвольное число, то a^p–1–1 делится на p (без остатка). Например, поскольку 17 – простое число, то, согласно его утверждению, все числа

кратны 17. Очевидно, 17¹⁶–1 придется пропустить: это число никак не может быть кратно 17, поскольку оно на единицу меньше такого числа, а именно 17¹⁶. Ферма понимал, что такое дополнительное условие необходимо, но не упомянул этого в письме. Проверим такой случай:

и, разделив это число на 17, получим 1 085 102 592 571 150 095 ровно. Как вам такое?

Этот любопытный факт в настоящее время называют Малой теоремой Ферма, в отличие от Последней (или Великой) теоремы. Ферма был одним из пионеров теории чисел, изучающей глубокие свойства целых чисел. Как в его время, так и в последующие три столетия теория чисел представляла собой самую что ни на есть чистую математику. Она не имела важных применений, и было непохоже, чтобы они когда-нибудь появились. Один из ведущих специалистов Великобритании по чистой математике Годфри Харольд Харди, несомненно, думал именно так, о чем и заявил в своем небольшом шедевре – эссе «Апология математика», опубликованном в 1940 году. Теория чисел была для Харди одной из любимых областей математики, и в 1938 году он вместе с Эдвардом Мейтлендом Райтом выпустил классический труд «Введение в теорию чисел». В нем можно найти и Малую теорему Ферма – это Теорема 71 в главе VI. Мало того, вся глава, по существу, рассказывает о ее следствиях.

Политические и математические взгляды Харди отражали веяния, преобладавшие в то время в высших кругах академического сообщества, и сегодня представляются в значительной мере предвзятыми, но стиль изложения у него легок и элегантен, а кроме того, его статьи позволяют лучше понять академический менталитет тех времен, что тоже весьма ценно. Некоторые из изложенных им взглядов актуальны и сегодня. Харди говорил, что «писать о математике – сплошная тоска для профессионального математика. Математик должен делать что-то значимое, доказывать новые теоремы, чтобы расширять математические знания, а не рассказывать о том, что сделал он сам или другие математики». Такой вот своеобразный подход к «распространению знаний», так высоко ценимому сегодня в академическом мире, но именно он превалировал в общении с неспециалистами еще 40 лет назад.

Одна из причин, по которым Харди считал необходимым оправдывать свою профессию перед публикой, была в том, что, по его мнению, математика того сорта, которой он посвятил свою жизнь, никогда не имела полезных приложений и перспектив их обрести. Математика не оправдывала себя. Интерес Харди к ней был чисто интеллектуальным: удовлетворение от решения сложных задач и расширение абстрактного человеческого знания. Его не особенно беспокоила утилитарная полезность математики, но он испытывал по этому поводу легкое чувство вины. Однако его, как убежденного пацифиста, тревожила возможность использования математики в военных целях. Бушевала Вторая мировая война, а некоторые области математики всегда применялись в военном деле. Архимед, как говорят, использовал свойства параболы, чтобы сфокусировать солнечные лучи на вражеских кораблях и поджечь их, а рычаги – чтобы сконструировать громадную лапу, способную вытащить корабль из воды. Баллистика позволяет нам прицельно метать предметы – от каменных ядер до разрывных снарядов. Ракеты и дроны не могут достичь цели без помощи сложной математики, в частности теории управления. Но Харди был убежден, что его любимая теория чисел никогда – по крайней мере, еще очень-очень долго – не будет иметь военного применения, и гордился этим.

Харди писал в то время, когда типичный кембриджский «дон» (преподаватель) тратил около четырех часов в день на научные изыскания и, может быть, часок на работу со студентами, а остальное время отдыхал, заряжая свои интеллектуальные батарейки. Он смотрел крикет и читал газеты. Ему, по всей видимости, просто не приходило в голову, что даже ведущий математик-исследователь мог бы использовать свободное время с пользой и рассказывать неспециалистам, чем в настоящее время занимаются математики. Это позволило бы творить новую математику и параллельно писать о ней. Именно этим многие из нас, профессиональных математиков, занимаются сегодня.

Общее утверждение Харди о том, что значительная доля чистой математики не имеет практического применения и, вероятно, никогда не найдет его, остается верным{40}. Но вот при выборе конкретных примеров бесполезных тем он сильно рисковал попасть впросак. Сказав, что теория чисел и теория относительности еще много лет не смогут послужить никакой военной цели, он, что называется, попал пальцем в небо, хотя нужно признать, что его предсказание не исключало подобное применение полностью. Очень трудно решить заранее, какие идеи найдут применение, а какие нет. Научитесь делать это, и вы сможете без труда разбогатеть. Интересно, что именно те области, которые не кажутся практически применимыми, могут внезапно выскочить на передний план в промышленности, коммерции и, к несчастью, в военном деле. Именно это произошло с теорией чисел и конкретно с Малой теоремой Ферма, которая теперь стала основой того, что мы считаем абсолютно стойкими шифрами.

Ирония ситуации в том, что за два года до того, как Харди написал свою «Апологию…», глава британской контрразведки MI6 купил поместье Блетчли-парк, в котором в будущем должна была разместиться Правительственная школа кодирования и шифрования, секретный дешифровальный центр cоюзников во время Второй мировой войны. Там, как известно, криптоаналитики взломали шифр машины Enigma, которую Германия использовала в военных целях, и ряд других шифровальных систем стран Оси. Самый известный сотрудник Блетчли-парка Алан Тьюринг начал обучение в 1938 году и прибыл в школу в день объявления войны. Криптоаналитики Блетчли-парка использовали для взлома германских шифров неординарные подходы и математику, в том числе и идеи из теории чисел. Всего лишь через неполные 40 лет после этого произошла настоящая революция в криптографии, фундаментом которой стала теория чисел. Естественно, для новой криптографии нашлось не только гражданское, но и военное применение. Вскоре она приобрела принципиально важное значение для работы интернета. Сегодня мы сильно зависим от нее, по большей части даже не сознавая, что она существует.

Теория относительности тоже нашла свое место не только в гражданской, но и в военной сфере. Можно сказать, что она сыграла определенную роль в реализации Манхэттенского проекта по созданию атомной бомбы. В соответствии с популярной легендой, знаменитая формула Эйнштейна E = mc² убедила физиков, что в небольшом количестве вещества содержится громадное количество энергии. Это, конечно, сильное упрощение, которое использовалось после ударов по Хиросиме и Нагасаки для объяснения публике принципа действия такого оружия. Не исключено, что таким образом пытались также отвлечь внимание от настоящего секрета: физики ядерных реакций. Более близкий к нам пример – Глобальная система позиционирования, GPS (глава 11), точность которой зависит как от специальной, так и от общей теории относительности. Разработка системы финансировалась американскими военными, а сама она первоначально предназначалась исключительно для них.

Счет 2:0 в пользу военных.

Я совершенно не виню Харди. Он понятия не имел, что происходит в Блетчли-парке, и едва ли мог предугадать стремительный взлет цифровых вычислений и средств связи. Слово «цифровой» означает в основном работу с целыми числами, а ведь именно этим занимается теория чисел. Внезапно оказалось, что результаты, полученные многими поколениями специалистов по чистой математике исключительно из интеллектуального любопытства, теперь можно использовать для инновационной технологии. Сегодня в электронных устройствах, которые четверть рода человеческого ежедневно носит с собой, воплощен огромный пласт математики – и это не только теория чисел, но и многое другое, от комбинаторики до абстрактной алгебры и функционального анализа. Секретность онлайн-операций, осуществляемых частными лицами, компаниями, а также военными, обеспечивается хитроумными математическими преобразованиями, основанными на столь любимой Харди теории чисел. Это совсем не удивило бы Тьюринга, который был настолько впереди всех, что уже в 1950 году всерьез задумывался об искусственном интеллекте. Но Тьюринг был мечтателем. В те времена это было даже не научной фантастикой, а просто фантазией.

Код, или шифр, – это метод преобразования сообщения на обычном языке, то есть открытого текста, в зашифрованный текст, который выглядит как тарабарщина. При этом преобразовании, как правило, используется ключ – принципиально важная часть информации, которую держат в секрете. Говорят, например, что Юлий Цезарь пользовался шифром, в котором каждая буква алфавита сдвигалась на три позиции. «Три» здесь и есть ключ. Такой тип шифра подстановки, в котором каждая буква алфавита заменяется на другую букву по постоянному правилу, несложно взломать, если в вашем распоряжении имеется достаточное количество шифровок. Для этого достаточно знать частоты, с которыми буквы алфавита встречаются в открытом тексте. Тогда можно сделать достаточно достоверное предположение о принципе шифрования и проверить его. Поначалу будут встречаться ошибки, но если часть текста вдруг расшифруется как JULFUS CAESAR, то легко догадаться, что на месте F должна быть I.

Каким бы простым и ненадежным ни казался шифр Цезаря, он служит хорошим примером для иллюстрации общего принципа, который до недавнего времени лежал в основе практически всех систем шифрования. Это симметричный шифр, то есть и отправитель, и получатель пользуются, по существу, одним и тем же ключом. Я говорю «по существу», потому что они пользуются им по-разному: Юлий сдвигает алфавит на три позиции вправо, а получатель сдвигает его на три позиции в обратном направлении. Однако если вы знаете, как ключ используется при шифровании, то легко можете обратить процесс вспять и использовать тот же ключ для расшифровки. Даже весьма хитроумные и надежные шифры симметричны. Поэтому безопасность требует, чтобы используемый ключ держался в секрете от всех, за исключением отправителя и получателя сообщений.

Как сказал Бенджамин Франклин, «трое могут сохранить секрет, если двое из них мертвы». В симметричном шифре ключ должны знать как минимум двое, что, по мнению Франклина, слишком много. В 1944 или 1945 году кто-то (возможно, Клод Шеннон, изобретатель теории информации) в исследовательском центре Bell Labs в США предложил защищать голосовую связь от подслушивания при помощи добавления к сигналу случайного шума, а затем, после получения сигнала, его вычитания. Это тоже симметричный метод, поскольку ключ здесь – случайный шум и вычитание компенсирует его добавление. В 1970 году Джеймс Эллис, инженер Центра правительственной связи Великобритании, бывшей Правительственной школы кодирования и шифрования, заинтересовался, нельзя ли генерировать шум математически. Если да, то в принципе можно создать систему, где это будет результатом не простого добавления сигналов, а математического процесса, который очень трудно обратить, даже если знать, что он собой представляет. Конечно, получатель должен иметь возможность обратить процесс, но этого можно добиться с помощью второго ключа, известного только получателю.

Эллис назвал свою идею «несекретным шифрованием». Сегодня используют термин «криптосистема с открытым ключом». Обе эти фразы означают, что правило для шифрования сообщения можно свободно опубликовать в общедоступных источниках, но без знания второго ключа никто не сможет понять, как обратить эту процедуру и расшифровать сообщение. Оставалась единственная проблема: Эллис не смог разработать подходящий метод шифрования. Он хотел получить то, что сегодня называется функцией с потайным входом: легко вычислить, но трудно обратить (в потайной вход легко провалиться, но трудно выбраться). Как всегда, здесь должен иметься секретный второй ключ, позволяющий законному получателю обратить процесс так же легко, как спрятанная лестница позволяет провалившемуся выбраться.

И тут на сцену выходит Клиффорд Кокс, британский математик, также работавший в Центре правительственной связи. В сентябре 1973 года Кокса неожиданно осенила блестящая идея. Он понял, что мечту Эллиса можно реализовать, создав функцию с потайным входом при помощи простых чисел. С точки зрения математики перемножить два или более простых числа легко. Можно, например, вручную перемножить два 50-значных простых числа, получив при этом 99– или 100-значный результат. Обратная операция – взять 100-значное число и найти его простые делители – намного труднее. Стандартный школьный метод «пробовать все возможные делители по очереди» здесь бесполезен: возможностей слишком много. Кокс придумал функцию, основанную на произведении двух больших простых чисел, то есть на результате их перемножения. Получившийся шифр настолько надежен, что это произведение (но не его простые сомножители) можно не держать в секрете. Для расшифровки необходимо знать эти два простых числа по отдельности, в них и кроется секретный второй ключ. Без этих чисел вы ничего не сможете сделать, знания только их произведения недостаточно. Допустим, я говорю вам, что нашел два простых числа, произведение которых равно

Сможете ли вы найти эти простые числа?{41} По-настоящему быстрый суперкомпьютер сможет это сделать, а вот ноутбук вряд ли. А если взять побольше знаков, то и суперкомпьютер выйдет из игры.

Итак, Кокс, до этого занимавшийся теорией чисел, придумал метод создания функции с потайным входом с помощью пары простых чисел – как он это сделал, я объясню чуть позже, когда мы познакомимся с необходимыми понятиями. Метод был настолько прост, что поначалу Кокс даже не записал его. Позже он изложил идею подробно в отчете для начальства. В то время никто не мог представить, как применить этот метод с тогдашними слабыми компьютерами, поэтому его засекретили. Кроме того, его передали в Агентство национальной безопасности США. Обе организации видели военный потенциал метода, потому что даже при медленных расчетах можно было переслать ключ к какому-то совершенно иному шифру по электронной связи. Это основной способ применения подобных шифров на сегодняшний день как в военных, так и в гражданских целях.

Британские бюрократы не раз не могли разглядеть гигантские перспективы предлагаемых новинок, взять хотя бы пенициллин, реактивный двигатель, ДНК-идентификацию. В данном случае, однако, они могут оправдать свои действия патентным правом: чтобы получить патент, необходимо раскрыть суть изобретения. Как бы то ни было, революционную идею Кокса положили под сукно подобно тому, как в финале фильма «Индиана Джонс: В поисках утраченного ковчега» ящик с ковчегом отправляют на гигантский правительственный склад, до самой крыши забитый одинаковыми ящиками.

Однако в 1977 году появился точно такой же метод, который независимо придумали и быстро опубликовали три американских математика: Рональд Ривест, Ади Шамир и Леонард Адлеман. Теперь в их честь эта система называется криптосистемой Ривеста – Шамира – Адлемана (RSA). В конце концов, в 1997 году британские службы безопасности рассекретили работу Кокса, и мы теперь знаем, что именно он первым додумался до этого.

Теория чисел появляется в криптографии сразу же, как только мы понимаем, что любое сообщение может быть представлено числом. Для шифра Цезаря это число есть положение буквы в алфавите, которое математики предпочитают обозначать числами от 0 до 25 (речь, конечно, идет о латинском алфавите), а не от 1 до 26, из соображений алгебраического удобства. Таким образом, A – это 0, B – это 1 и т. д., вплоть до Z = 25. Числа за пределами этого диапазона могут быть приведены к числам внутри него посредством прибавления или вычитания чисел, кратных 26. Это соглашение закольцовывает все 26 букв алфавита, так что после Z мы вновь возвращаемся к A. Тогда шифр Цезаря может быть сведен к простому математическому правилу, более того, к формуле

Обратный процесс выглядит очень похоже:

Именно это делает данный шифр симметричным.

Мы можем изобретать новые шифры, меняя правила, или формулу. Нам нужен лишь простой способ превращения сообщения в число и две формулы: одна для превращения открытого текста в зашифрованный и вторая для его расшифровки. Каждая из формул должна быть обратной по отношению к другой.

Существует множество способов превращать открытый текст в числа. Простой способ состоит в том, чтобы использовать для каждой буквы числа 0–25 и выстраивать эти числа в ряд, добавляя к числам 0–9 нулик, чтобы получилось 00–09. Тогда JULIUS превратится в 092011082018 (не забывайте, A = 00). Возможно, потребуются дополнительные числа для пробела, знаков пунктуации, ну и т. д. Правило, которое превращает одно число в другое, называется теоретико-числовой функцией.

Замыкание чисел в кольцо – стандартный фокус теории чисел, известный как модулярная арифметика. Выберем число – здесь это 26. Теперь представим, что 26 – это все равно что 0, так что из всех чисел вам потребуются только числа от 0 до 25. В 1801 году Карл Фридрих Гаусс в своей знаменитой книге «Арифметические исследования» (Disquisitiones Arithmeticae) указал, что в такой системе можно складывать, вычитать и умножать числа, руководствуясь обычными законами алгебры и не выходя за пределы выбранного диапазона 0–25. Просто производите обычные вычисления с обычными числами, а затем возьмите остаток от деления результата на 26. Так, 23 × 17 = 391, что равно 15 × 26 + 1. Остаток равен 1, поэтому в этом необычном варианте арифметики 23 × 17 = 1.

Эта идея работает и при замене 26 любым другим числом; число это называют модулем, и мы можем подписать (mod 26), чтобы подчеркнуть происходящее. Таким образом, если быть точными, мы вычислили, что 23 × 17 = 1 (mod 26).

Но как насчет деления? Если мы разделим это равенство на 17 и не будем слишком заморачиваться тем, что все это означает, то получим

Таким образом, разделить на 17 – все равно что умножить на 23. Мы теперь можем придумать новое правило шифрования:

обратной формулой к этому будет

Это правило сильно перемешивает алфавит и расставляет буквы в следующем порядке:

Это по-прежнему шифр подстановки на уровне отдельных букв, так что его несложно взломать, но он наглядно показывает, что мы можем менять формулу. Кроме того, он иллюстрирует использование модулярной арифметики – а это ключ к обширным областям теории чисел.

Однако деление может оказаться более хитрым делом. Поскольку 2 × 13 = 26 = 0 (mod 26), мы не можем делить на 13, в противном случае мы бы получили, что 2 = 0/13 = 0 (mod 26), что неверно. То же относится и к делению на 2. Общее правило таково, что мы можем делить на любое число, не имеющее общих простых делителей с модулем. Поэтому 0 исключается, но это не удивительно: на 0 нельзя делить и обычные целые числа. Если модулем является простое число, мы можем делить на любое число меньше модуля, за исключением 0.

Преимущество модульной арифметики заключается в том, что она придает списку открытых «слов» алгебраическую структуру. Это открывает широкий спектр правил для преобразования открытого текста в зашифрованный и обратно. Кокс, а позже Ривест, Шамир и Адлеман просто выбрали очень умное правило.

Шифровать сообщение по одной букве, используя для каждой буквы всегда одинаковое численное обозначение, не слишком надежно: каким бы ни было правило, шифр все равно остается шифром подстановки. Но если поделить сообщение на блоки длиной, скажем, букв по 10, а сегодня скорее по 100, и превратить каждый блок в число, то мы получим шифр подстановки по блокам. Если взять достаточно длинные блоки, то легко различимой закономерности в частоте их встречаемости не будет, так что расшифровать текст путем наблюдения за тем, какие числа встречаются чаще других, не удастся.

Кокс и Ривест – Шамир – Адлеман выводили свои правила из красивой теоремы, открытой Ферма в 1640 году, которая показывает, как ведут себя степени чисел в модулярной арифметике. Говоря современным языком, Ферма рассказал своему другу де Бесси, что если n – простое число, то

для любого числа a. «Я продемонстрировал бы тебе это, если бы не боялся, что получится слишком длинно», – писал Ферма. Эйлер получил недостающее доказательство в 1736 году, а в 1763 году он опубликовал более общую теорему, которая применима, если модуль не является простым числом. Теперь a и n не должны иметь общий делитель, а степень n – 1 во втором варианте формулы заменена на функцию Эйлера φ(n). Нам нет нужды знать, что это такое{42}, но необходимо понимать, что если n = pq есть произведение двух простых чисел p и q, то φ(n) = (p – 1)(q – 1).

Криптосистема RSA действует следующим образом:

• Найдите два больших простых числа p и q.

• Вычислите произведение n = pq.

• Вычислите φ(n) = (p – 1)(q – 1). Держите это в секрете.

• Выберите число e, не имеющее общих простых делителей с φ(n).

• Вычислите d так, чтобы de = 1 (mod φ(n)).

• Число e можно раскрыть. (Кстати говоря, это дает очень мало полезной информации о φ(n).)

• Сохраните d в секрете. (Это принципиально важно.)

• Пусть r – текстовое сообщение, зашифрованное как число по модулю n.

• Конвертируйте r в зашифрованный текст r^e (mod n). (Правило шифрования также можно раскрыть.)

• Чтобы расшифровать r^e, следует возвести его в степень d (mod n). (Не забываем, что d секретно.) Это дает (r^e)^d, что равно r^ed, что равно r по теореме Эйлера.

Здесь правило шифрования звучит как «возвести в e-ю степень»:

а правило расшифровки как «возвести в d-ю степень»:

Кое-какие математические фокусы, в которые я не буду вдаваться, дают возможность производить все эти действия быстро (на современных компьютерах) при условии, что вам известны p и q по отдельности. Самое неприятное – то, что если они вам неизвестны, то знание n и e не сильно помогает в вычислении d, необходимого для расшифровки сообщения. По существу, вам нужно найти простые делители p и q числа n, что, как мы видели (судя по всему), намного труднее, чем перемножить p и q и найти таким образом n.

Иными словами, «возведение в степень e» и есть требуемая функция с потайным входом.

В настоящее время все вышеописанное может быть проделано за минуту или около того на обычном ноутбуке для, скажем, 100-значных простых чисел p и q. Одна из приятных особенностей системы RSA состоит в том, что по мере того, как компьютеры становятся более мощными, достаточно всего лишь увеличивать p и q. Метод по-прежнему будет работать.

Один из недостатков системы – то, что RSA, будучи полностью реализуемой и практичной, все же слишком медленна, чтобы рутинно использовать ее для шифрования полного текста каждого сообщения. Основное ее реальное применение – это безопасная передача секретного ключа для какой-то совершенно иной системы шифрования, гораздо более быстрой в использовании и надежной при условии, что ключ никому не известен. Так что RSA решает проблему раздачи ключей, которая мучила криптографию с начала времен. Одним из факторов, позволивших расшифровать код Enigma, было то, что определенные установки машины Enigma передавались операторам в начале каждого дня небезопасным способом. Еще одно распространенное применение системы RSA – проверка электронной подписи, то есть шифрованного сообщения, устанавливающего личность отправителя.

Начальник Кокса Ральф Бенджамин, научный руководитель, главный инженер и директор Центра правительственной связи, прекрасно знал свое дело и сразу обратил внимание на эту возможность. Он написал в рапорте: «Я считаю ее очень важной для военного применения. В быстро меняющейся военной ситуации можно встретить непредвиденные угрозы или возможности. Тот, кто может раздавать свой ключ быстро при помощи электронных средств связи, получает серьезное преимущество перед противником». Но компьютеры тех времен не могли выполнить эту задачу, и британское правительство упустило, как позже оказалось, громадные возможности.

Математические методы редко оказываются пригодными для решения практических задач, что называется, в готовом виде. Как и все остальное, их, как правило, приходится адаптировать и приспосабливать, чтобы преодолеть возникающие трудности. Это относится и к системе RSA: она все же не так проста, как я здесь описал. На самом деле, стоит прекратить восхищаться идеей и задуматься, что может пойти не так, как на поверхность вылезает множество интереснейших теоретических вопросов для математиков.

Несложно показать, что вычислить φ(n), не зная его простых множителей p и q, так же трудно, как и найти сами p и q. Мало того, их нахождение представляется единственным способом сделать это. Так что главный вопрос состоит в следующем: насколько трудна факторизация, то есть разложение на простые сомножители? Большинство математиков считает эту задачу чрезвычайно трудной в техническом смысле: время выполнения любого алгоритма разложения на простые множители с ростом числа знаков в произведении pq растет взрывным образом. (Кстати говоря, причина использования именно двух простых чисел, а, скажем, не трех, кроется в наибольшей сложности этого варианта. Чем больше простых сомножителей имеет число, тем проще найти один из них. Разделите на него, и число станет заметно меньше, а найти остальные сомножители будет проще.) Однако никто в настоящее время не может доказать, что разложение на простые множители – трудная задача. Никто не знает, с какой стороны подойти к поиску такого доказательства. Так что надежность метода RSA зиждется на недоказанной гипотезе.

Остальные вопросы и подводные камни касаются тонкостей метода. Неудачный выбор используемых чисел может сделать RSA уязвимой для особенно хитроумных атак. Например, если e слишком мало, то мы можем определить сообщение r, вычислив корень e-й степени из зашифрованного текста r^e как из обычного числа, то есть не по модулю n. Еще одна потенциальная уязвимость возникает, если одно и то же сообщение рассылается e получателям с использованием одной и той же степени e, даже если p и q для каждого из них свои. В этом случае может быть применено красивое утверждение, известное как китайская теорема об остатках, которое позволит раскрыть текст сообщения.

Говорят также, что метод RSA семантически небезопасен. Это означает, что, в принципе, он может быть взломан, если зашифровать с его помощью множество разных сообщений и попытаться сопоставить полученные результаты с шифрованным текстом, который нужно взломать. По существу, это метод проб и ошибок. Для длинных сообщений это, возможно, непрактично, но если рассылается множество коротких посланий, то такой метод дешифровки может сработать. Чтобы избежать этого, RSA модифицируют добавлением к сообщению лишних цифр по какой-то конкретной, но случайной схеме. Это делает текст длиннее и позволяет избежать многократной отправки одного и того же сообщения.

Еще при одном методе взлома шифров RSA используется не математический недостаток метода, а физическая особенность компьютера. В 1995 году криптограф и предприниматель Пол Кохер заметил, что если криптоаналитик хорошо знает используемое оборудование и может измерить, сколько времени уходит на дешифровку нескольких сообщений, то он может легко установить секретный ключ d. В 2003 году Дэн Боне и Дэвид Брамли продемонстрировали практический вариант такой атаки на примере сообщений, отправленных по традиционной сети с использованием стандартного протокола SSL (Secure Sockets Layer).

Существование математических методов, которые иногда способны очень быстро разложить на простые множители большое число, подразумевает, что простые числа p и q должны выбираться так, чтобы они удовлетворяли некоторым ограничениям. Они не должны быть слишком близкими, иначе можно будет применить известный метод, восходящий еще к Ферма. В 2012 году группа под руководством Арьена Ленстры опробовала этот метод на миллионах открытых ключей, извлеченных из интернета, и смогла взломать каждый 500-й из них.

Очень серьезно изменило бы ситуацию появление реального рабочего квантового компьютера. Эти машины, не вышедшие еще из младенческого состояния, вместо обычных двоичных цифр 0 и 1 используют квантовые биты и в принципе могут производить гигантские расчеты, такие как разложение на простые множители громадных чисел, с беспрецедентной скоростью. Я немного отложу рассказ о них.

Система RSA лишь один из множества шифров, основанных на теории чисел или ее близком родиче, комбинаторике, то есть методе подсчета числа способов, посредством которых может быть получена определенная комбинация, без перечисления всех этих способов. Если хотите убедиться в том, что математический источник идей в сфере криптографии еще не пересох, то посмотрите на альтернативную систему шифрования, которая использует одну из наиболее глубоких и интересных областей сегодняшней теории чисел. Эта область исследует эллиптические кривые, которые, наряду с другими вещами, стали основой для доказательства Великой теоремы Ферма, предложенного Эндрю Уайлсом.

Со времен Ферма теория чисел серьезно продвинулась вперед. То же произошло и с алгеброй, где акцент сместился с символьного представления неизвестных чисел на общие свойства символьных систем, определяемых конкретными правилами. Эти две области исследований в значительной мере перекрываются. Кое-какие интереснейшие идеи о тайных шифрах появились на стыке двух специальных разделов алгебры и теории чисел: конечных полей и эллиптических кривых. Чтобы понять, о чем идет речь, для начала нужно разобраться, что это такое.

Мы видели, что в арифметике по некоторому модулю можно складывать, вычитать и умножать «числа», подчиняясь при этом обычным алгебраическим правилам. Чтобы не отвлекаться, я не стал перечислять эти правила, но типичными их примерами могут служить переместительный (коммутативный) ab = ba и сочетательный (ассоциативный) (ab)c = a(bc) законы умножения. Аналогичные законы существуют и для сложения. Распределительный (дистрибутивный) закон a(b + c) = ab + ac тоже выполняется, и есть еще простые правила относительно 0 и 1, такие как 0 + a = a и 1a = a. Любая система, в которой выполняются эти законы, называется кольцом. Если в системе возможно также деление (кроме деления на 0) и стандартные правила выполняются, мы получаем поле. Эти названия традиционны, заимствованы из немецкого и означают просто «некий набор вещей, подчиняющихся обозначенным правилам». Целые числа по модулю 26 образуют кольцо, известное как Z₂₆. Мы видели, что там есть проблемы с делением на 2 и 13, так что это не поле. Я сказал (не поясняя почему), что целые числа по простому модулю не имеют подобных проблем, так что Z₂, Z₃, Z₅, Z₇ и т. д. – целые числа по модулю 2, 3, 5, 7 и т. д. – все являются полями.

Обычные целые числа продолжаются до бесконечности и образуют бесконечное множество. Такие системы, как Z₂₆ и Z₇, напротив, конечны. Первая из них включает в себя только числа 0–25, а вторая – числа 0–6. Первая представляет собой конечное кольцо, вторая – конечное поле. Конечные числовые системы, если они не слишком велики, очень хорошо подходят для компьютерных вычислений, потому что те могут проводиться точно. Поэтому неудивительно, что на основе конечных полей построено множество различных кодов. Это не только криптографические шифры, которые должны обеспечивать секретность, но и коды распознавания и коррекции ошибок, задача которых – обеспечить прием сообщений без ошибок, возникающих из-за случайного «шума», такого как электрические помехи. Этими вопросами занимается целая новая область математики – теория кодирования.

Простейшими конечными полями являются Z_p, целые числа по простому модулю p. Тот факт, что они образуют поле, был известен (хотя и не в такой формулировке) Ферма. Французский революционер Эварист Галуа, убитый на дуэли в 20-летнем возрасте, доказал, что это не единственные существующие конечные поля. Он нашел их все: существует одно конечное поле для каждой простой степени pⁿ, и содержит оно ровно pⁿ различных «чисел». (Предупреждение: если n больше 1, это поле не является полем целых чисел по модулю pⁿ.) Таким образом, существуют конечные поля с 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 23, 25, … элементами, но не с 1, 6, 10, 12, 14, 15, 18, 20, 21, 22, 24, … элементами. Очень любопытная теорема.

Эллиптические кривые (с эллипсами они связаны лишь очень опосредованно) зародились в другой области – в классической теории чисел. Около 250 года древнегреческий математик Диофант Александрийский написал трактат о решении алгебраических уравнений с использованием натуральных (или рациональных) чисел. Например, знаменитый треугольник 3–4–5 имеет прямой угол, спасибо Пифагору, потому что 3² + 4² = 5². Следовательно, эти числа являются решением Пифагорова уравнения x² + y² = z². Одна из теорем Диофанта показывает, как найти все решения этого уравнения в долях и, в частности, в натуральных числах. Область в целом, где речь идет о решении уравнений в рациональных числах, получила известность как диофантовы уравнения. Ограничение до рациональных чисел меняет правила игры; например, x² = 2 может быть решено в действительных числах, но не в рациональных.

Одна из задач Диофанта звучит так: «Разделить заданное число на два числа, произведение которых равно кубу за вычетом его стороны». Если первоначальное число равно a, мы можем разбить его на Y и a – Y, и тогда нам потребуется решить уравнение

Диофант исследовал случай, когда a = 6. Подходящая замена переменных (вычесть 9, заменить Y на y + 3, а X на – x) превращает это уравнение в

Отсюда он вывел решение X = 17/9, Y = 26/27.

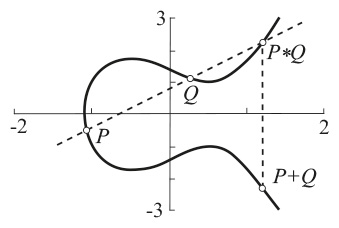
Чтобы «сложить» две точки P и Q на эллиптической кривой, соедините их прямой, которая пересечет кривую в третьей точке P*Q. Затем постройте точку, симметричную данной относительно оси x, это и будет P + Q

Интересно, что аналогичные уравнения появились в геометрии, когда математики попытались использовать аналитический метод (продвинутый вариант дифференциального и интегрального исчисления) для расчета длины дуги сегмента эллипса. Именно отсюда берет начало термин «эллиптическая кривая». Ученые знали, как найти ответ на аналогичный вопрос для окружности с использованием интегрального исчисления, так что задача сводилась к нахождению интеграла функции, в которой присутствовал квадратный корень из квадратного многочлена, а это можно сделать при помощи (обратных) тригонометрических функций. Этот же метод в применении к эллипсу дает интеграл функции, в которой присутствует квадратный корень из кубического многочлена, и после нескольких бесплодных экспериментов стало ясно, что необходим какой-то новый класс функций. Эти функции оказались довольно красивыми, хотя и сложными и получили наименование эллиптических функций из-за их связи с длиной дуги эллипса. Квадратный корень из кубического многочлена есть решение y уравнения

(любое слагаемое с x² может быть превращено в 0 при помощи эквивалентных преобразований). В координатной геометрии это уравнение определяет кривую на плоскости, так что такие кривые (и их алгебраический вариант в виде уравнения) стали называть эллиптическими кривыми.

Если коэффициенты целые, мы можем рассмотреть данное уравнение в модулярной арифметике, скажем в Z₇. Каждое решение в обычных целых числах приведет нас к решению в арифметике по модулю 7. Поскольку эта система конечна, можно воспользоваться методом проб и ошибок. Для диофантова уравнения y² = x³ – x + 9 мы быстро обнаруживаем все его решения (mod 7):

Из этих решений можно сделать вывод, обязательный для любого решения в обычных целых числах: по модулю 7 любое решение должно сводиться к одному из этих шести. То же относится и к рациональным решениям при условии, что знаменатель у них не кратен 7 – такие решения запрещены, поскольку в Z₇ такой знаменатель превращается в 0. Если заменить 7 на какое-нибудь другое число, то можно получить больше информации о форме любого рационального решения.

Теперь мы смотрим на эллиптические кривые – уравнения – через призму конечных колец и полей. Геометрический образ кривой здесь, по существу, неприменим, поскольку имеется всего лишь конечное множество точек, но нам удобно пользоваться прежним названием. На рисунке показана типичная фигура и ее дополнительное свойство, известное еще Ферма и Эйлеру и интриговавшее математиков в начале XX века. Имея два решения, можно «сложить» их, чтобы получить еще одно решение, как показано на рисунке. Если решения – рациональные числа, то рациональным числом будет и их сумма. Это не просто «купи два, получи третье бесплатно», а «купи два, получи бесплатно уйму всего», потому что операцию и построение можно повторить. Иногда это вновь приводит нас в одну из начальных точек, но в основном подобные действия генерируют бесконечно много различных решений. Мало того, эти решения имеют красивую алгебраическую структуру: они образуют группу Морделла – Вейля эллиптической кривой. Луис Морделл доказал ее основные свойства, а Андре Вейль обобщил их. Слово «группа» здесь означает, что дополнение подчиняется короткому списку простых правил. Эта группа коммутативна, то есть P + Q = Q + P, что очевидно из рисунка, поскольку прямая, проведенная через P и Q, совпадает с прямой, проведенной через Q и P. Существование такой групповой структуры – явление необычное, и большинство диофантовых уравнений не может этим похвастаться. Многие из них вовсе не имеют решений, некоторые имеют всего по несколько, и трудно предсказать, какое именно уравнение находится перед вами. В настоящее время эллиптические кривые находятся в центре интенсивных исследований – по этой и другим причинам. Доказывая Великую теорему Ферма, Эндрю Уайлс доказал глубокую гипотезу об эллиптических кривых, которая стала одним из ключевых этапов доказательства.

Групповая структура эллиптической кривой интересует и криптографов. Обычно она рассматривается как форма «дополнения» к решениям, хотя формула там намного сложнее, потому что она коммутативна, и символ + стал традиционным в теории коммутативных групп. В частности, если есть решение (x, y), которое можно рассматривать как точку на плоскости, то мы можем генерировать решения P + P, P + P + P и т. д. Естественно называть такие решения 2P, 3P и т. д.

В 1985 году Нил Коблиц и Виктор Миллер независимо друг от друга поняли, что можно применить этот групповой закон к эллиптической кривой, чтобы получить шифр. Идея в том, чтобы работать в конечном поле с большим числом элементов. Чтобы зашифровать P, мы получаем kP для очень большого целого числа k, что несложно сделать при помощи компьютера, и называем результат Q. Чтобы обратить этот процесс, мы должны начать с Q и найти P – по существу, разделить Q на k. Из-за сложности групповой формулы обратный расчет очень труден, так что мы придумали новый тип «односторонней» функции с потайным входом, а следовательно, новую криптосистему с открытым ключом. Этот подход известен как шифрование на основе эллиптических кривых, или ECC (Elliptic Curve Cryptography). Точно так же, как RSA может применяться с использованием множества разных простых чисел, ECC может применяться с использованием множества разных эллиптических кривых над множеством разных конечных полей, с разным выбором P и множителя k. Здесь опять же имеется секретный ключ, который позволяет выполнить быструю расшифровку.

Преимущество этой системы в том, что относительно небольшая группа дает шифр, соответствующий по надежности шифру RSA, основанному на значительно больших простых числах. Так что шифр на основе эллиптических кривых более эффективен. Шифровать сообщение и расшифровывать его – при условии, что вам известен секретный ключ, – тоже оказывается быстрее и проще. Взломать шифр, если ключ вам неизвестен, трудно. В 2005 году Агентство национальной безопасности США рекомендовало перенести исследования по криптографии с открытыми ключами в новую область эллиптических кривых.

Как и в случае RSA, не существует строгого доказательства надежности системы ECC. Диапазон возможных атак аналогичен диапазону атак, осуществляемых в отношении RSA.

В настоящее время наблюдается серьезный интерес к криптовалютам, которые представляют собой финансовые системы, не контролируемые традиционными банками, хотя банки тоже начинают интересоваться ими. Банки – они такие: всегда начеку, всегда в поисках новых способов делать деньги. Самая известная криптовалюта – биткоин. Надежность биткоинов обеспечивается таким методом, как блокчейн, который представляет собой шифрованную запись всех транзакций с участием конкретной «монеты» (coin). Новые биткоины появляются в результате майнинга, который, по существу, означает выполнение громадного количества бессмысленных в остальном вычислений. Майнинг биткоинов потребляет значительное количество электроэнергии без какой бы то ни было полезной цели, за исключением обогащения нескольких индивидов. В Исландии, где электричество очень дешево благодаря геотермальным электростанциям, на майнинг биткоинов уходит больше электричества, чем используют все домохозяйства страны, вместе взятые. Вряд ли эта деятельность помогает бороться с глобальным потеплением и климатическим кризисом, но дело обстоит именно так.

Биткоин и многие другие криптовалюты используют одну и ту же эллиптическую кривую под заковыристым названием secp256k1. Ее уравнение, y² = x³ + 7, запоминается гораздо легче, и это кажется главной причиной ее выбора. Шифрование через secp256k1 основано на одной из точек на этой кривой, заданной координатами

Это наглядно показывает, какие гигантские целые числа задействованы в практических реализациях ECC.

Я уже несколько раз говорил, что надежность системы RSA зиждется на недоказанном предположении о трудоемкости разложения числа на простые множители. Даже если это предположение верно, – а очень похоже, что это действительно так, – не исключено существование и других способов дискредитации надежности шифра (то же самое можно сказать обо всех классических схемах шифрования с открытым ключом). В их числе – появление компьютера, работающего намного быстрее нынешних. Сегодня эта новая угроза безопасности связи уже маячит на горизонте: речь идет о квантовом компьютере.

Классическая физическая система имеет конкретное состояние. Монета на столе может лежать орлом или решкой кверху. Выключатель либо включен, либо выключен. Двоичная цифра (или бит) в памяти компьютера равна либо 0, либо 1. Квантовая система не такова. Квантовый объект – это волна, а волны могут накладываться одна на другую, что на формальном языке называется суперпозицией. Состояние суперпозиции – это смесь состояний компонентов. Знаменитый (мало того, печально знаменитый) кот Шрёдингера может служить ярким примером: при помощи хитроумного устройства с радиоактивным атомом и ампулой ядовитого газа в сочетании с котом в непроницаемом ящике можно добиться того, что квантовое состояние несчастного животного будет суперпозицией состояний «жив» и «мертв». Классический кот должен находиться в одном из этих состояний, а квантовый может находиться в обоих одновременно.

Пока вы не откроете ящик.

Тогда волновая функция кота схлопывается, или коллапсирует, в одно из классических состояний. Кот либо жив, либо мертв. Любопытство (вы же открыли ящик) губит кота. Или не губит.

Я не хочу углубляться в неоднозначные и часто весьма жаркие споры о том, действительно ли квантовые состояния сработали бы подобным образом в случае представителя кошачьего племени{43}. Для нас важно лишь, что математическая физика прекрасно работает для более простых объектов, которые уже используются для создания рудиментарных квантовых компьютеров. Вместо бита, который может быть равен 0 или 1, там мы имеем кубит, который равен 0 и 1 одновременно. Классический компьютер, который может стоять у вас или у меня на столе, лежать в сумке или в кармане, работает с информацией, представленной в виде последовательности нулей и единиц. Он даже использует для этого квантовые эффекты – настолько мал масштаб электронных схем в сегодняшних компьютерах, но суть в том, что все вычисления соответствуют классической физике. При конструировании классических компьютеров инженеры очень стараются сделать так, чтобы нуль всегда оставался нулем, а единица – единицей и чтобы они никогда не встречались. Классический кот может быть либо жив, либо мертв. Так что регистр из (скажем) восьми бит может хранить в себе единственную последовательность вида 01101101 или 10000110.

В квантовом компьютере происходит в точности противоположное. Регистр из восьми кубитов может хранить оба эти варианта одновременно, наряду с остальными 254 возможными 8-битовыми последовательностями. Более того, он может производить арифметические действия со всеми 256 возможными вариантами одновременно. Это как если бы у вас было 256 компьютеров вместо одного. Чем длиннее последовательности, тем сильнее растет число возможностей: 100-битный регистр может содержать единственную последовательность из 100 бит, а 100-кубитный регистр может хранить все 10³⁰ возможных 100-битных последовательностей и при этом манипулировать ими. Это и есть «параллельная обработка данных» в крупном масштабе, и именно это так волнует и восхищает многих в квантовых компьютерах. Вместо того чтобы производить 10³⁰ операций по очереди, одну за другой, вы производите их все разом.

В принципе.

В 1980-е годы Пол Бениофф предложил квантовую модель машины Тьюринга – теоретической основы классических вычислений. Вскоре после этого физик Ричард Фейнман и математик Юрий Манин указали, что квантовый компьютер будет способен производить громадное количество вычислений параллельно. Серьезный прорыв в теории квантового компьютера произошел в 1994 году, когда Питер Шор придумал очень быстрый квантовый алгоритм для разложения больших чисел на простые множители. Из этого следует, что криптосистема RSA потенциально уязвима для атак противника, использующего квантовый компьютер, но, что еще важнее, квантовый алгоритм может серьезно превзойти алгоритм классический в решении осмысленной, неискусственной задачи.

На практике на пути к созданию квантового компьютера нас ждут просто громадные препятствия. Крохотные возмущения от внешних источников или даже просто тепловые колебания молекул вызывают декогеренцию, то есть разрушение состояния суперпозиции, причем очень быстрое. Для смягчения этой проблемы машину в настоящее время приходится охлаждать до температуры, очень близкой к абсолютному нулю (–273 ℃), что требует использования гелия-3 – редкого побочного продукта ядерных реакций. Но даже это не может предотвратить декогеренцию, а лишь замедляет ее. Так что каждое вычисление приходится дополнять системой коррекции ошибок, которая замечает нарушения, вызванные помехами от внешних источников, и возвращает кубиты в то состояние, в котором они должны находиться. Квантовая пороговая теорема утверждает, что такой метод работает при условии, что система способна исправлять ошибки быстрее, чем декогеренция их вызывает. По приблизительной оценке, вероятность ошибки для каждого логического ключа не должна превышать одну тысячную.

Коррекция ошибок имеет свою цену: она требует больше кубитов. Например, чтобы разложить на простые множители число, которое может храниться в n кубитах с использованием алгоритма Шора, на процесс вычисления требуется время, примерно пропорциональное чему-то промежуточному между n и n². С учетом коррекции ошибок, совершенно необходимой на практике, время становится более похожим на n³. Для 1000-кубитного числа коррекция ошибок увеличивает время расчета в тысячу раз.

До последнего времени никому не удавалось построить квантовый компьютер больше чем с несколькими кубитами. В 1998 году Джонатан Джонс и Мишель Моска использовали 2-кубитное устройство для решения задачи Дойча, которая сформулирована в работе Дэвида Дойча и Ричарда Джоза 1992 года. Это квантовый алгоритм, работающий экспоненциально быстрее любого традиционного алгоритма, он всегда дает ответ, и этот ответ всегда верен. Решает он следующую задачу. Нам дано гипотетическое устройство (оракул), которое реализует булеву функцию, превращающую любую n-значную битовую строку в 0 или в 1. Математически оракул и есть эта функция. Нам также сообщили, что эта булева функция принимает значение либо 0 всюду, либо 1 всюду, либо 0 ровно на половине битовых строк и 1 на другой половине. Задача – определить, какой из этих трех вариантов имеет место, применяя функцию к битовым строкам и наблюдая результат. Задача Дойча носит намеренно искусственный характер и представляет собой скорее доказательство концепции, нежели что-то практическое. Ее достоинство в том, что она представляет собой конкретную задачу, при решении которой квантовый алгоритм доказуемо превосходит любой традиционный. Строго говоря, она доказывает, что класс сложности EQP (точные решения за полиномиальное время на квантовом компьютере) отличается от класса P (точные решения за полиномиальное время на традиционном компьютере).

В том же 1998 году появилась и 3-кубитная машина, а в 2000 году – машины с 5 и 7 кубитами. В 2001 году Ливен Вандерсипен с коллегами{44} реализовал алгоритм Шора, используя в качестве квантовых битов семь ядер со спином 1/2 в специально синтезированной молекуле. Этими ядрами можно было манипулировать при комнатной температуре с помощью методов управления ядерным магнитным резонансом неустойчивых состояний. Ученым удалось найти простые делители целого числа 15. Большинство из нас может проделать эту операцию в уме, но это стало важным доказательством концепции. К 2006 году исследователи увеличили число кубитов до 12, а в 2007 году компания D-Wave сообщала даже про 28 кубитов.

Пока все это происходило, исследователи смогли сильно увеличить промежуток времени, в течение которого можно поддерживать квантовое состояние, прежде чем оно декогерирует. В 2008 году один кубит удалось сохранить в атомном ядре больше секунды. К 2015 году время жизни кубита составляло уже шесть часов. Сравнивать эти промежутки времени трудно, потому что в разных устройствах использовались разные квантовые методы, но прогресс в любом случае был впечатляющим. В 2011 году D-Wave объявила, что создала коммерчески доступный квантовый компьютер D-Wave One со 128-кубитным процессором. В 2015 году D-Wave утверждала, что преодолела рубеж в 1000 кубитов.

Первой реакцией на заявления D-Wave было недоверие. Архитектура устройства была необычной, и у некоторых возникли вопросы: действительно ли это настоящий квантовый компьютер, а не навороченный классический компьютер, использующий околоквантовое оборудование. Во время испытаний он превосходил стандартные классические компьютеры на полезных задачах, но при этом был специально сконструирован для таких задач, тогда как классические компьютеры, с которыми он состязался, – нет. Его преимущества, казалось, исчезали, если классические компьютеры специально конструировались для соответствующих задач. Споры продолжаются до сих пор, но машины D-Wave используются и неплохо работают.

Ключевой целью исследований является квантовое превосходство: создание квантового устройства, которое превосходит по производительности лучшие классические компьютеры по крайней мере на одном расчете. В 2019 году команда Google AI опубликовала статью в Nature под заголовком «Квантовое превосходство с использованием программируемого сверхпроводящего процессора»{45}. Она объявила, что создала квантовый процессор под названием Sycamore с 54 кубитами, но один из них отказал, что снизило их количество до 53. С его помощью за 200 секунд решили задачу, на решение которой у классического компьютера ушло бы 10 000 лет.

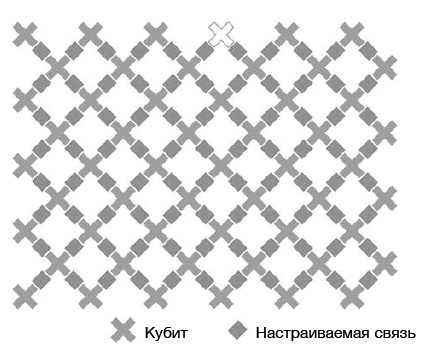
Архитектура квантового процессора Sycamore

Это заявление сразу же было поставлено под сомнение по двум причинам. С одной стороны, этот расчет предположительно мог быть выполнен классической машиной за более короткое время. С другой, Sycamore решал довольно надуманную задачу: получение выборки выходных последовательностей псевдослучайной квантовой схемы. Устройство соединяет компоненты схемы случайным образом, а цель всего этого – рассчитать распределение вероятностей выборки возможных выходных последовательностей. Одни выходные последовательности оказываются гораздо более вероятными, чем другие, так что это распределение получается очень сложным и неоднородным. Время классического расчета с ростом числа кубитов увеличивается экспоненциально. Тем не менее команде ученых удалось достичь своей главной цели: показать, что не существует практических препятствий для создания квантового компьютера, способного превзойти классический в чем-нибудь.

Сразу возникает вопрос: как удостовериться в том, что ответ верен? Ведь невозможно ждать 10 000 лет, пока классический компьютер решит задачу, и нельзя просто верить результату без всякой проверки. Исследователи справились с этой проблемой при помощи метода, известного как сравнительный анализ с перекрестной энтропией. Он предполагает сравнение вероятностей конкретных битовых строк с теоретическими вероятностями, рассчитанными на классическом компьютере. Это позволяет оценить, насколько велика вероятность того, что полученный результат верен. Исследователи пришли к выводу, что результат точен с погрешностью до 0,2 % с очень высокой («пять сигм») вероятностью.

Несмотря на прогресс, большинство экспертов уверены, что до практической реализации идеи квантового компьютера нам еще далеко. Некоторые сомневаются даже, что его вообще можно создать. Физик Михаил Дьяконов написал:

Возможно, Дьяконов и прав, но другие с ним не согласны. Так или иначе, даже призрачная возможность того, что кто-то – скорее всего, многочисленная группа исследователей, финансируемая правительством или крупной корпорацией, – справится с созданием квантового компьютера, заставляет службы безопасности многих стран и финансовых институтов видеть ночные кошмары. Недруги тогда смогут расшифровать секретные сообщения, а преступники – разрушить систему интернет-торговли и банкинга. Поэтому теоретики ломают головы над тем, как могла бы выглядеть криптография в постквантовом мире, и пытаются сыграть на опережение и обеспечить безопасность коммуникаций.

К счастью, то, что квантовый компьютер может взломать, он же может сделать нераскрываемым. Для этого потребуются новые криптографические методы, использующие квантовые расчеты для создания шифров, которые не сможет взломать даже квантовый компьютер. Это потребует нового взгляда на математику, лежащую в основе вычислений. Как ни странно, в значительной мере это все та же теория чисел, хотя и более современная, чем у Ферма.

Теоретически неминуемое наступление квантовых компьютеров породило волну исследований, нацеленных на создание методов шифрования, которые не могут быть взломаны квантовым компьютером. Не так давно Национальный институт стандартов и технологии США запустил программу постквантовой криптографии с целью идентификации классических криптосистем, находящихся в зоне риска, и поиска новых способов борьбы с их уязвимостями. В 2003 году Джон Прус и Кристоф Залка{46} оценили уязвимость системы RSA и криптографии на основе эллиптических кривых для квантового компьютера, работающего по алгоритму Шора. В 2017 году Мартин Реттелер с коллегами{47} дополнил их результаты. Исследователи доказали, что в случае эллиптической кривой над конечным полем с q элементами, где q примерно равно 2ⁿ, RSA уязвима для квантового компьютера с числом кубитов 9n + 2 log₂n +10 и схемы из не более чем 448n³ log₂n +4090n³ вентилей Тоффоли. Вентиль Тоффоли – особый тип логической схемы. Из вентилей Тоффоли можно строить схемы, выполняющие любую логическую функцию. Более того, эта схема обратима: зная выходные данные, можно, пройдя по ней в обратном направлении, вычислить вход. В настоящее время стандартом для RSA является использование числа из 2048 бит, то есть около 616 десятичных знаков. По оценке этой команды исследователей, 2048-битная RSA будет уязвима для квантового компьютера с n = 256, а шифрование на основе эллиптической кривой – для квантового компьютера с n = 384.

Распознавать уязвимости – это, конечно, замечательно, но главный вопрос в том, что следует делать для защиты. Решение этой задачи требует совершенно новых криптографических методов. Общая идея их та же, что всегда: метод шифрования должен основываться на трудных математических задачах с возможностью какого-нибудь простого обхода. Но теперь «трудный» означает «трудный для квантового компьютера». В настоящий момент обнаружено четыре основных класса задач такого рода:

• Случайные линейные шифры с коррекцией ошибок.

• Решение систем нелинейных уравнений над большими конечными полями.

• Нахождение коротких векторов в многомерных решетках.

• Нахождение маршрутов между случайными вершинами псевдослучайного графа.

Рассмотрим кратко четвертый из этих вариантов, где задействованы новейшие идеи и очень продвинутая математика.

Для практических целей возьмем граф, который имеет около 10⁷⁵ вершин и соответственно большое число ребер. Шифр зависит от нахождения пути через этот граф между двумя конкретными вершинами. Это одна из разновидностей задачи коммивояжера, имеющая сопоставимую с ней трудность. Чтобы создать в решении этой задачи обходной путь, граф должен иметь скрытую структуру, которая делает решение простым. Центральная идея состоит в использовании так называемых суперсингулярных изогенных графов, или SIG. Они образуются с использованием эллиптических кривых, которые называют суперсингулярными. Вершины такого графа соответствуют всем суперсингулярным эллиптическим кривым над алгебраическим замыканием конечного поля с p элементами. Существует примерно p/12 таких кривых.

Изогения между двумя эллиптическими кривыми – это полиномиальное отображение одной из них на другую, сохраняющее структуру группы Морделла – Вейля. Мы используем изогении для определения ребер графа. Для этого следует взять второе простое число q. Ребра этого графа соответствуют изогениям q-й степени между двумя эллиптическими кривыми, соответствующими концам данного ребра. Из каждой вершины исходит ровно q + 1 ребер. Такие графы называются экспандерами, или расширяющими, это означает, что случайные пути, начинающиеся в любой вершине, быстро расходятся после их начала, по крайней мере на протяжении большого числа шагов.

Граф-экспандер может быть использован для создания функции хеширования – булевой функции, формирующей из n-битных строк m-битные, где m много меньше n. Алиса может использовать хеш-функцию, чтобы убедить Боба, что она знает конкретную n-битную строку, известную также и Бобу, не раскрывая самой строки. Для этого она формирует намного более короткую хеш-функцию этой строки и отправляет ее Бобу. Боб вычисляет хеш-функцию своей строки и сравнивает.

Для того чтобы этот метод надежно работал, необходимо выполнить два условия. Одно из них – это условие потайного входа, известное как стойкость к восстановлению прообраза: с вычислительной точки зрения невозможно обратить хеш-функцию и найти n-битную строку, которая дает данный хеш. В общем случае таких строк существует множество, но дело в том, что на практике невозможно найти ни одной. Второе условие – стойкость функции хеширования к коллизиям. Это означает, что с вычислительной точки зрения невозможно найти две разные n-битные строки с одним и тем же m-битным хешем. Раз так, то даже если Ева – любительница подслушивать (или устройство перехвата сообщений) – сумеет подслушать разговор, то хеш, который Алиса пересылает Бобу, не поможет ей разобраться, что представляла собой первоначальная n-битная строка.

Если у нас имеется два простых числа p и q, удовлетворяющие дополнительным формальным условиям, мы можем воспользоваться этой идеей, построив соответствующий SIG, а затем использовать его свойства экспандера, чтобы определить стойкую как к восстановлению прообраза, так и к коллизиям функцию хеширования. Эту функцию можно использовать для создания высоконадежного шифра. Взлом такого шифра требует вычисления множества изогений между эллиптическими кривыми. Лучший квантовый алгоритм для одного такого расчета выполняется за время p^1/4. Сделайте p и q достаточно большими (математика подсказывает, насколько большими), и вы получите криптосистему, которую не сможет взломать даже квантовый компьютер.

Все это выглядит очень заумно. Вряд ли вы разобрались во всех деталях, тем более что большую их часть я опустил. Но, я надеюсь, вы поняли главное: чтобы успешно защитить личную, коммерческую и военную связь от любителей подслушивать, вооруженных гипотетическими сегодня, но вполне реальными в скором времени квантовыми компьютерами, нам потребуется не что иное, как очень продвинутая и абстрактная математика, имеющая отношение к алгебраической геометрии над конечными полями.

Теория чисел, столь любимая Харди, оказалась куда более полезной, чем он мог вообразить. Но некоторые из сегодняшних ее применений наверняка разочаровали бы его. Думается, нам следовало бы извиниться перед ним за это.