Это база: Зачем нужна математика в повседневной жизни

10 Улыбнитесь, пожалуйста!

Каждый год человечество загружает в интернет около триллиона фотографий. Судя по этой цифре, мы излишне оптимистично оцениваем интерес других людей к нашим отпускным селфи, родившемуся в семье ребенку и другим объектам, некоторые из которых даже упоминать не стоит. А снимают сейчас все: делается это быстро и просто, а в телефоне у каждого имеется камера. В работе и производстве этих камер огромную роль играет математика. Крохотные высокоточные объективы – настоящее чудо техники, невозможное без сложнейшей математической физики, связанной с преломлением света трехмерными телами с изогнутыми поверхностями. В этой главе я хочу сосредоточиться всего на одном аспекте современной фотографии: сжатии изображений. Цифровые камеры, самостоятельные или встроенные в телефон, хранят очень подробные изображения в виде двоичных файлов. Создается впечатление, что карты памяти способны хранить больше информации, чем должно на них помещаться. Как же удается заключить так много детальных картинок в небольшой компьютерный файл?

Фотографические изображения содержат много избыточной информации, которую можно удалить без потери точности. Математика позволяет делать это тщательно выстроенными способами. Стандарт JPEG в небольших цифровых камерах типа «навел и щелкнул», который до самого недавнего времени был самым распространенным форматом файлов и до сих пор используется очень широко, предусматривает пять математических преобразований, выполняемых последовательно. В них задействован дискретный фурье-анализ, алгебра и теория шифрования. Все эти преобразования заложены в программное обеспечение камеры, которое сжимает данные, прежде чем записать их на карту памяти.

Если, конечно, вы не предпочитаете данные в формате RAW – по существу, это непосредственно то, что камера считала с матрицы. Емкость карт памяти растет так быстро, что сжимать файлы уже нет абсолютной необходимости. Но в этом случае вам в конечном итоге приходится манипулировать изображениями объемом по 32 мегабайта каждое, тогда как раньше они имели вдесятеро меньший размер, да и в «облако» такие файлы загружаются много медленнее. Стоит ли этим заморачиваться, зависит от того, кто вы и для чего нужны фотографии. Если вы профессионал, это для вас, надо полагать, важно. Если вы турист, как и я, и снимаете все подряд, то можете получить хороший снимок тигра и в двухмегабайтном JPEG-файле.

Сжатие изображений – важная часть более общего вопроса сжатия данных, который, несмотря на громадные технологический успехи, по-прежнему остается жизненно важным. Каждый раз, когда интернет следующего поколения становится в 10 раз быстрее и приобретает еще более впечатляющую пропускную способность, какой-нибудь гений изобретает новый формат данных (скажем, трехмерное видео сверхвысокой четкости), требующий куда больше данных, чем прежде, и все возвращается на круги своя.

Иногда у нас просто нет другого выбора, кроме как выжимать каждый байт пропускной способности из канала связи. На Марсе 4 января 2004 года что-то свалилось с неба, ударилось о поверхность и отскочило. Если говорить точнее, то марсианский ровер A под названием Spirit подскочил над марсианским грунтом 27 раз. Он был со всех сторон окружен надувными баллонами, как будто завернут в эдакую космическую пузырчатую пленку – последнее слово в методах посадки. После общей проверки систем и различных процедур инициализации ровер пустился исследовать поверхность чужой планеты, где к нему вскоре присоединился компаньон, Opportunity. Оба ровера работали необычайно успешно и прислали на Землю громадное количество данных. Тогда же математик Филип Дэвис указал, что в этой программе многое зависит от математики, но «общественность вряд ли это сознает». Оказалось, что не сознает этого не только общественность. В 2007 году датские аспиранты-математики Уффе Янквист и Бьёрн Толдбод посетили Лабораторию реактивного движения в Пасадене с журналистской миссией: раскрыть роль математики в программе Mars Rover. И услышали в ответ:

– Мы ничего такого не делаем. На самом деле мы не используем никакой абстрактной алгебры, теории групп, ничего подобного.

Это встревожило молодых людей, и один из них спросил:

– За исключением кодирования канала?

– Там используется абстрактная алгебра?

– Коды Рида – Соломона основаны на полях Галуа.

– Это для меня новость.

На самом деле в космических программах NASA задействована очень и очень продвинутая математика для сжатия данных и их кодирования таким способом, который позволяет исправлять ошибки, неизбежно возникающие при передаче. Это просто приходится делать, когда передатчик находится чуть ли не в миллиарде километров от Земли и имеет мощность электрической лампочки. (Немного помогает передача данных через аппарат на орбите Марса, такой как Mars Odissey или Mars Global Surveyor.) Большинству инженеров нет нужды это знать, они и не знают. В этой ситуации, как в зеркале, отражается неверное представление широкой общественности о математике.

Все в вашем компьютере, будь то электронная почта, фото-, видео– или аудиоальбом, хранится в памяти как поток двоичных цифр, битов, нулей и единиц. Восемь бит образуют байт, а 1 048 576 байт – мегабайт. Типичная фотография низкого разрешения занимает около 2 Мб. Хотя все цифровые данные записываются именно в этом виде, разные приложения используют разные форматы, так что смысл данных зависит от приложения. Каждый тип данных имеет скрытую математическую структуру, и удобство обработки часто оказывается куда более значимым, нежели размер файла. Удобный формат данных может означать их избыточность – использование для их хранения больше битов, чем реально требует содержание информации. Это создает возможность сжатия данных посредством устранения избыточности.

Письменный (и устный) язык весьма и весьма избыточен. В качестве доказательства можно привести фразу, уже встретившуюся нам в этой главе, удалив при этом каждый пятый знак:

Надо полагать, вы можете разобрать, что в ней говорится, без особых размышлений или усилий. Оставшейся информации достаточно, чтобы восстановить первоначальную фразу целиком.

Тем не менее эта книга будет намного легче восприниматься зрительно, если не заставлять издателей экономить на краске, пропуская каждый пятый знак. Правильные слова мозгу обрабатывать намного проще, потому что именно это он обучен делать. Однако если вы хотите передать битовую строку, вместо того чтобы обрабатывать эти данные при помощи какого-то приложения, эффективнее будет переслать более короткую последовательность нулей и единиц. Уже на заре развития теории информации такие ее пионеры, как Клод Шеннон, поняли, что избыточность информации дает возможность закодировать сигнал с использованием меньшего числа битов. Мало того, Шеннон вывел формулу, позволяющую вычислить, насколько короче код может получиться из данного сигнала для данного уровня избыточности.

Избыточность принципиально важна, потому что сообщения без нее невозможно сжать без потери информации. Доказательство основано на простом подсчете. Предположим, например, что нас интересуют сообщения длиной 10 бит, такие как 1001110101. Существует ровно 1024 таких битовых строки. Предположим, мы хотим сжать 10 бит данных в 8-битную строку. Таких строк существует ровно 256. Так что сообщений у нас имеется вчетверо больше, чем сжатых строк, и невозможно каждой 10-битной строке поставить в соответствие 8-битную строку так, чтобы разным 10-битным строкам соответствовали разные 8-битные строки. Если каждая 10-битная строка может встретиться с равной вероятностью, то выясняется, что у нас нет умного способа обойти это ограничение. Однако если некоторые из 10-битных строк встречаются очень часто, а остальные очень редко, мы можем выбрать код, который обозначит короткими битовыми строками (скажем, по 6 бит) самые часто встречающиеся сообщения и более длинными строками (может быть, по 12 бит) – редкие сообщения. 12-битных строк существует много, так что их недостаток нам не грозит. Всякий раз, когда встречается редкое сообщение, оно добавляет два бита к длине передачи, зато когда встречается частое сообщение, оно убавляет четыре бита. При подходящих вероятностях из сообщений будет отнято больше бит, чем добавлено.

Вокруг подобных методов выросла целая отрасль математики – теория кодирования. В общем случае эти методы куда тоньше, чем описанный выше, и обычно в них для определения кодов используются свойства абстрактной алгебры. Это не должно слишком удивлять: в главе 5 мы видели, что, по существу, коды – это математические функции и что особенно полезны здесь функции теории чисел. Там целью была секретность, здесь цель – сжатие данных, но общий принцип одинаков в обоих случаях. Алгебра имеет отношение к структуре, как и избыточность.

Сжатие данных, а следовательно, и сжатие изображений, использует избыточность для создания кодов, укорачивающих данные конкретного типа. Иногда данные сжимаются «без потерь»: в этом случае первоначальную информацию можно восстановить по сжатой версии в точности. Иногда данные теряются, и тогда восстановленный вариант лишь приближение первоначальных данных. Это было бы плохо, скажем, для банковских счетов, но зачастую вполне годится для изображений: главное – устроить все так, чтобы приближенный вариант по-прежнему выглядел для человеческого глаза похожим на первоначальное изображение. Тогда информация, которая теряется безвозвратно, вообще не имеет значения.

Изображения в реальном мире по большей части избыточны. Отпускные фотки часто содержат большие блоки голубого неба, нередко примерно одинакового оттенка по всей площади, так что множество пикселей с одинаковым цветовым кодом может быть заменено двумя парами координат для противоположных углов прямоугольника и коротким кодовым сообщением типа «окрасить эту область этим оттенком голубого цвета». Такой метод сжимает изображения без потерь. Реально его не применяют, но он наглядно показывает, почему сжатие без потерь возможно.

Я старомоден, то есть пользуюсь фототехникой, которой – какой ужас! – уже около 10 лет. Возмутительно! Я умею обращаться с техникой и вполне могу снять что-то с помощью смартфона, но это не превратилось в рефлекс, и в серьезные путешествия, такие как сафари с тиграми в национальных парках Индии, я беру с собой маленькую автоматическую цифровую камеру. Она создает файлы изображений с такими названиями, как IMG_0209.JPG. Идентификатор JPG свидетельствует о том, что файлы сохранены в формате JPEG, по первым буквам названия Joint Photographic Expert Group, и указывает на систему сжатия данных. JPEG – отраслевой стандарт, хотя с годами он получил некоторое развитие и теперь существует в нескольких формально разных формах.

Формат JPEG{59} предполагает выполнение не менее пяти последовательных преобразований, большинство из которых сжимает данные, полученные на предыдущем этапе (первоначальные сырые данные на первом этапе). Остальные перекодируют их для дальнейшего сжатия. Цифровые изображения состоят из миллионов крохотных квадратиков, именуемых пикселями – элементами картинки (на английском слово pixel расшифровывается как picture element). Сырые данные с камеры присваивают каждому пикселю битовую строку, представляющую как цвет, так и яркость. Обе величины представляются как доли трех компонентов: красного, зеленого и синего. Низкие доли всех трех компонентов соответствуют бледным цветам, высокие – темным. Эти числа конвертируются в три связанных друг с другом числа, которые лучше соответствуют тому, как человеческий мозг воспринимает изображения. Первое из них – светлота – дает общую яркость изображения и измеряется числами от черного, через все более светлые оттенки серого, до белого. Если удалить информацию о цвете, у вас останется старомодное черно-белое изображение – на самом деле это множество оттенков серого. Другие два числа, известные как цветность, представляют собой разности между светлотой и количеством синего и красного света соответственно.

Символьно, если R – красный, G – зеленый и B – синий, то начальные числа для R, G и B заменяются светлотой R + G + B и двумя цветностями (R + G + B) – B = R + G и (R + G + B) – R = G + B. Если вы знаете R + G + B, R + G и G + B, то можете вычислить R, G и B, так что этот этап проходит без потерь.

Реализовать второй этап без потерь не удастся. Здесь данные цветности урезаются до меньших значений за счет огрубления разрешения. Один только этот этап снижает размер файла данных наполовину. Это приемлемо, потому что в сравнении с тем, что «видит» камера, зрительная система человека более чувствительна к яркости и менее – к цветовым различиям.

Третий этап наиболее математичен. Он сжимает информацию светлости с использованием цифровой версии преобразования Фурье, которую мы встречали в главе 9 в связи с медицинскими сканерами. Там оригинальное преобразование Фурье, которое превращает сигналы в составляющие их частоты и наоборот, было модифицировано, чтобы представлять проекции черно-белых изображений. На этот раз мы представляем сами черно-белые изображения, но в простом цифровом формате. Изображение разбивается на крохотные блоки 8 × 8 пикселей, так что в каждом из них присутствуют 64 возможных значения светлости, по одному на каждый пиксель. Дискретное косинусное преобразование – цифровой вариант преобразования Фурье – представляет это черно-белое изображение 8 × 8 как суперпозицию 64 стандартных изображений с коэффициентами. Эти коэффициенты суть амплитуды соответствующих изображений, а сами изображения выглядят как полосы и клетки разной ширины. Таким образом может быть получен любой блок 8 × 8 пикселей, так что этот этап тоже проходит без потерь. Во внутренних координатах эти блоки представляют собой дискретные версии cos mx cos ny для разных целых m и n, где x меняется по горизонтали, а y – по вертикали, и оба они принимают значения от 0 до 7.

Хотя дискретное преобразование Фурье реализуется без потерь, его нельзя назвать бессмысленным, потому что именно оно делает возможным четвертый этап. Этот этап опять же основан на недостаточной чувствительности человеческого зрения, которая порождает избыточность. Если яркость или цвет меняется на большой площади изображения, мы это замечаем. Если они меняются на очень небольших участках, зрительная система сглаживает эффект, и мы видим лишь среднее. Именно поэтому печатные изображения воспринимаются как картинки, хотя при ближайшем рассмотрении они представляют оттенки серого россыпью черных точек на белой бумаге. Эта особенность человеческого зрения означает, что узоры с очень тонкими полосками менее важны, так что их амплитуды могут быть записаны с меньшей точностью.

64 базовых паттерна дискретного косинусного преобразования

Пятый этап – это технический прием, известный как «код Хаффмана», для более эффективной записи амплитуд 64 базовых паттернов. Дэвид Хаффман придумал этот метод в 1951 году еще студентом. Он тогда получил задание написать курсовую работу по оптимально эффективным двоичным кодам, но не мог доказать, что хотя бы какой-нибудь из существовавших на тот момент кодов оптимален. Уже собираясь сдаться, Хаффман придумал новый метод, а затем и доказал, что он является наилучшим из возможных. Грубо говоря, задача в том, чтобы закодировать множество символов при помощи двоичных строк, а затем использовать их как словарь для кодирования сообщения. Сделать это необходимо так, чтобы минимизировать общую длину закодированного сообщения.

Например, в качестве словарных символов можно использовать буквы алфавита. В английском алфавите их 26, так что каждой из них можно было бы присвоить 5-битную строку, скажем, A = 00001, B = 00010 и т. д. Пять бит нужны потому, что из четырех бит можно составить только 16 строк. Но использовать 5-битные строки было бы неэффективно, потому что на буквы, которые встречаются редко, такие как Z, уходит ровно столько же битов, сколько на распространенные буквы, такие как E. Лучше было бы присвоить E короткую строку, такую как 0 или 1, и постепенно удлинять строки по мере того, как буквы становятся менее вероятными. Однако, поскольку в этом случае кодовые строки получаются разными по длине, потребуется дополнительная информация, которая сообщит реципиенту, где следует разбить строку на отдельные буквы. В принципе, это можно сделать при помощи префикса перед кодовой строкой, но у нас сам код должен быть, как говорят математики, беспрефиксным: кодовая строка не должна начинаться с другой, более короткой кодовой строки. Редко используемые буквы, такие как Z, при этом требуют намного больше битов, но, поскольку они редкие, более короткие строки для E с лихвой компенсируют это. Общая длина типичного сообщения оказывается короче.

В коде Хаффмана это достигается формированием «дерева» – своеобразного графа, не имеющего замкнутых петель и очень распространенного в информатике, потому что такой граф представляет целую стратегию решений типа да/нет, где каждое решение зависит от предыдущего. Листьями дерева являются символы A, B, C, …, и из каждого листа выходит по две ветви, соответствующие двум битам 0 и 1. Каждый лист обозначен числом, которое называют его весом и которое показывает, как часто встречается соответствующий символ. Дерево строится шаг за шагом путем слияния двух наименее частых листьев в новый «материнский» лист, тогда как первые два листа становятся листьями-«дочками». Материнскому листу присваивается вес, равный сумме весов двух дочерних листьев. Этот процесс продолжается до тех пор, пока все символы не сольются. Тогда кодовая строка для символа считывается с пути, который ведет по дереву к этому символу.

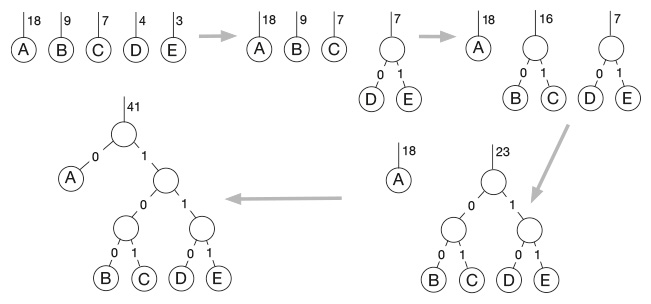
Построение кода Хаффмана

Например, на рисунке слева вверху показаны пять символов A, B, C, D, E и числа 18, 9, 7, 4, 3, указывающие на частоту их встречаемости. Самые редко встречающиеся символы здесь D и E. На втором этапе, вверху по центру, их смешивают с образованием материнского листа (ненумерованного) с весом 4 + 3 = 7, а символы D и E становятся дочерними. Две ведущие к ним ветви получают обозначения 0 и 1. Этот процесс повторяется несколько раз, пока все символы не сливаются воедино (внизу слева). Теперь мы считываем кодовые строки, следуя по путям вниз по дереву. К A ведет одна-единственная ветвь, обозначенная как 0. К B ведет путь 100, к C – путь 101, к D – путь 110 и к E – путь 111. Обратите внимание, что A, самый часто встречающийся символ, получает короткий путь, а менее распространенные символы – более длинные пути. Если бы вместо этого мы использовали код с фиксированной длиной строки, нам потребовалось бы по крайней мере три бита, чтобы закодировать пять символов, потому что двухбитных строк всего четыре. Здесь же в самых длинных строках по три бита, но в самой часто встречающейся – всего один, так что в среднем этот код более эффективен. Эта процедура гарантирует, что наш код беспрефиксный, поскольку любой путь на дереве ведет к какому-нибудь символу и на нем останавливается. Он не может продолжаться до другого символа. Более того, начав с наименее распространенных символов, мы гарантируем, что к самым распространенным символам будут вести самые короткие пути. Это отличная идея, легкая в программировании и очень простая концептуально, стоит один раз в ней разобраться.

Когда ваша камера создает файл JPEG, ее электроника производит все расчеты на лету, как только вы нажимаете на спуск. Процесс сжатия проходит не без потерь, но большинство из нас никогда этого не заметит. В любом случае экраны компьютеров и принтеры при распечатке не передают цвета и яркость в точности, за исключением случаев, когда их заранее тщательно калибруют. Непосредственное сравнение оригинального изображения и его сжатой версии делает различия более очевидными, но даже в этом случае только эксперт заметит разницу, если файл был сжат до 10 % от первоначального объема. Обычные смертные замечают разницу, только когда файл уменьшается до примерно 3 % от оригинала. Так что JPEG позволяет записать на карту памяти в 10 раз больше изображений, чем оригинальный формат данных RAW. Описанная выше сложная пятиступенчатая процедура, выполняемая в мгновение ока за кулисами, – это и есть магия, в которой задействованы пять областей математики.

Другой способ сжатия изображений вырос в конце 1980-х годов из фрактальной геометрии. Фрактал, как вы помните, это геометрическая фигура, структура которой детализируема на всех масштабах, как у береговой линии или облака. С фракталом связано определенное число, называемое размерностью и представляющее собой меру того, насколько данный фрактал угловат или волнист. Как правило, размерность фрактала не является целым числом. Полезный класс математически разрешимых фракталов включает самоподобные фракталы: небольшие их кусочки, надлежащим образом увеличенные, выглядят в точности так же, как более крупные куски целого. Классический пример – папоротник, состоящий из десятков листов, каждый из которых выглядит как миниатюрный папоротник. Самоподобные фракталы могут быть представлены математической структурой, известной как система итерированных функций (IFS). Это набор правил, говорящих, как следует сжимать копии формы и сдвигать получившиеся плитки так, чтобы они сложились и образовали целое. Фрактал можно восстановить по этим правилам, а для размерности фрактала существует даже формула.

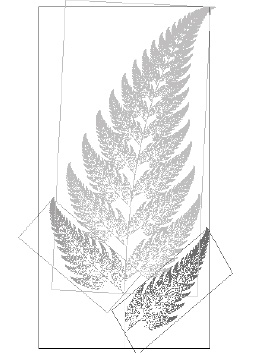
Фрактальный папоротник, составленный из трех преобразованных копий самого себя

В 1987 году математик Майкл Барнсли, давно увлекавшийся фракталами, понял, что их главное свойство может стать основой для нового метода сжатия изображений. Вместо того чтобы использовать огромное количество данных для кодирования каждой крохотной детали папоротника, можно просто закодировать соответствующую систему итерированных функций, на что потребуется значительно меньше данных. Программное обеспечение всегда может восстановить изображение папоротника по IFS. Барнсли вместе с Аланом Слоуном основал компанию Iterated Systems Inc., которая получила более 20 патентов. В 1992 году она совершила настоящий прорыв: был разработан автоматический метод нахождения подходящих правил IFS. Программа ищет на изображении маленькие области, которые можно рассматривать как съежившиеся версии бо́льших по размеру областей. Таким образом, она использует намного больше плиток для мощения изображения. Однако метод остается общим и применим к любым изображениям, а не только к тем из них, которые очевидно самоподобны. Фрактальное сжатие изображений не настолько популярно, как JPEG, по разным причинам, но использовалось в нескольких практических приложениях. Пожалуй, самым успешным из них была цифровая энциклопедия Encarta компании Microsoft, где все основные изображения были сжаты методом IFS.

Кто это? Прищурьтесь

На протяжении 1990-х годов компания предпринимала энергичные попытки распространить свой метод на сжатие видео, но из этого ничего не вышло, в основном потому, что тогдашние компьютеры были недостаточно быстрыми и имели недостаточно памяти. На сжатие одной минуты видео уходило 15 часов. Сегодня все изменилось, и фрактальное видеосжатие в отношении 200:1 можно проводить со скоростью один видеокадр в минуту. Повышение мощности компьютеров делает реальными и другие методы, и на данный момент от фрактального видеосжатия практически отказались. Но идея, лежащая в его основе, в свое время была полезна, да и сейчас таит в себе интересные возможности.

У людей есть очень странный прием для расшифровки некачественных изображений: мы прищуриваемся. Поразительно, но часто это помогает разобрать, что на самом деле изображено на картинке, особенно если она слегка размыта или если это компьютерное изображение с очень грубыми пикселями. Существует знаменитое изображение, составленное из 270 черных, белых и серых квадратов, которое создал в 1973 году Леон Хармон из Bell Labs для статьи о человеческом восприятии и компьютерном распознавании образов. Кто это? Если внимательно вглядеться в изображение, можно различить в нем что-то слегка напоминающее Авраама Линкольна, но если прищуриться, изображение начинает и правда походить на Линкольна.

Мы все это делаем, то есть знаем, что это работает, но вообще такой способ кажется безумием. Как можно улучшить плохую картинку, ухудшив собственное зрение? Отчасти ответ лежит в области психологии: прищуриваясь, мы переводим систему обработки визуальной информации в мозге в режим «плохое изображение», который, по всей видимости, запускает особые алгоритмы обработки изображений, развившиеся в ходе эволюции для работы с некачественными данными. Но есть и другая часть: как ни парадоксально, прищуривание выполняет роль своего рода предварительной обработки и очищает изображение в нескольких полезных отношениях. Так, оно размывает у Линкольна границы пикселей-квадратиков, так что портрет перестает походить на штабель серых строительных блоков.

Около 40 лет назад математики начали исследовать точный и гибкий эквивалент человеческого прищуривания, известный как вейвлет-анализ, или анализ формы сигнала. Этот метод применим не только к изображениям, но и к численным данным и первоначально был предложен для выделения структуры на конкретном пространственном масштабе. Вейвлет-анализ позволяет заметить лес, не обращая внимания на то, что он состоит из множества сложных деревьев и кустов.

Сначала математиками двигали в основном теоретические соображения: вейвлеты прекрасно годились для проверки научных гипотез о таких вещах, как турбулентный поток жидкости. Позже вейвлетам нашлись кое-какие чрезвычайно практические применения. В США Федеральное бюро расследований применяет вейвлеты для хранения дактилоскопических данных, и правоохранительные службы других стран следуют их примеру. Вейвлеты позволяют не просто анализировать изображения, а сжимать их.

В JPEG изображения сжимаются за счет отбрасывания информации, которая не слишком важна для человеческого зрения. Однако информация редко бывает представлена таким образом, что сразу становится очевидно, какие из битов можно считать лишними. Предположим, вы хотите отправить другу по электронной почте рисунок, сделанный на довольно грязном листе бумаги. Помимо собственно рисунка, на нем видно множество мелких черных пятнышек. Мы с вами, взглянув на этот рисунок, сразу понимаем, что эти пятнышки не важны, но сканер этого понять не может. Он просто сканирует лист, представляя изображение в виде длинной строки двоичных черно-белых сигналов, и не может определить, является ли какое-то черное пятнышко значимой частью рисунка или случайной помаркой. Некоторые «помарки», кстати говоря, могут в реальности оказаться зрачком далекой коровы или пятнышками мультяшного леопарда.

Главное препятствие заключается в том, что сигналы сканера не представляют данные об изображении в таком виде, который облегчал бы распознавание и устранение нежелательных элементов. Однако существуют и другие способы представления данных. Преобразование Фурье заменяет кривую списком амплитуд и частот, кодируя ту же самую информацию иначе. А когда данные представляются разными способами, то операции, которые сложны или невозможны в одном случае, могут стать простыми в другом. Например, вы можете взять телефонный разговор, применить к нему преобразование Фурье, а затем удалить все те части сигнала, фурье-компоненты которых имеют частоты слишком высокие или слишком низкие для человеческого уха. После этого вы можете применить к результату обратное преобразование Фурье и получить звук, идентичный с точки зрения человеческого восприятия оригиналу. Таким образом можно передавать больше разговоров по тому же каналу связи. Но в эту игру невозможно играть с оригинальным непреобразованным сигналом, поскольку у него нет «частоты» как очевидной характеристики.

Для некоторых целей метод Фурье обладает одним-единственным недостатком: синусовые и косинусовые компоненты продолжаются до бесконечности. Преобразование Фурье плохо представляет компактный сигнал. Единичный «всплеск» – простой сигнал, но для получения хотя бы умеренно убедительного всплеска требуются сотни синусов и косинусов. Проблема не в получении правильной формы всплеска, а в том, чтобы сделать все за его пределами равным нулю. Приходится избавляться от бесконечно длинных волнистых хвостов всех синусов и косинусов и, как следствие, добавлять еще более высокочастотные синусы и косинусы в отчаянной попытке компенсировать нежелательный мусор. В конечном итоге преобразованный вариант становится более сложным и требует больше данных, чем первоначальный всплеск.

Преобразование элементарных волн, или вейвлет-преобразование, полностью меняет ситуацию, поскольку использует в качестве базовых компонентов всплески (вейвлеты). Это непросто, и это нельзя сделать с любым подвернувшимся всплеском, но математику ясно, с чего следует начинать. Выбираем конкретную форму всплеска, которая будет служить материнским вейвлетом. Получаем дочерние вейвлеты (а также внучатые, правнучатые и т. д.), сдвигая материнский вейвлет вбок в различные позиции, а также расширяя или сжимая при помощи изменения масштаба. Чтобы представить более общую функцию, добавляем подходящие кратные этих вейвлетов на различных масштабах. Точно так же базовые синус и косинус фурье-преобразования являются «материнскими синусоидами», а синусы и косинусы всех остальных частот – дочерними по отношению к ним.

Слева: кривая синуса продолжается бесконечно. В центре: вейвлет локализован. Справа: еще три поколения

Вейвлеты придуманы для эффективного описания всплескоподобных данных. Более того, поскольку дочерние и внучатые вейвлеты представляют собой всего лишь отмасштабированные версии материнского, можно сосредоточиться на конкретных уровнях детализации. Если вы хотите устранить мелкомасштабную структуру, то удаляете все праправнучатые вейвлеты в вейвлет-преобразовании. Представьте себе превращение леопарда в вейвлеты – несколько крупных для тела, более мелкие для глаз, носа и пятен, затем совсем крохотные для шерстинок. Стремясь сжать эти данные, но сохранить их внешнее сходство с леопардом, вы решаете, что отдельные шерстинки не имеют значения, и удаляете все праправнучатые вейвлеты. Пятна остаются, и в целом все по-прежнему выглядит как леопард. Нечто подобное очень трудно – а то и вообще невозможно – сделать при помощи преобразования Фурье.

Подавляющая часть математических инструментов, необходимых для создания вейвлетов, существовала на тот момент в абстрактном виде уже полстолетия и даже больше в области функционального анализа. Когда вейвлеты получили известность, выяснилось, что заумный аппарат функционального анализа – это именно то, что требуется для их понимания и превращения в эффективный метод. Главным предварительным требованием для того, чтобы машина функционального анализа заработала, является хорошая форма материнского вейвлета. Мы хотим, чтобы все дочерние вейвлеты были математически независимы от матери, чтобы информация, закодированная матерью и дочерью, не перекрывалась и чтобы ни одна часть ни одной дочери не была избыточной. Говоря языком функционального анализа, мать и дочь должны быть ортогональны.

В начале 1980-х годов геофизик Жан Морле и специалист по математической физике Александр Гроссман предложили реалистичный материнский вейвлет. В 1985 году математик Ив Мейер доработал вейвлеты Морле и Гроссмана. Открытие, широко распахнувшее перспективы в этой области, сделала в 1987 году Ингрид Добеши. Предыдущие материнские вейвлеты выглядели надлежаще похожими на всплески, но все они имели крохотный математический хвостик, который волнами убегал в бесконечность. Добеши построила материнский вейвлет совсем без хвоста: за пределами определенного интервала мать всегда в точности равна нулю. Ее материнский вейвлет представлял собой настоящий всплеск, полностью заключенный в конечную область пространства.

Вейвлеты действуют как своего рода числовое увеличительное стекло, сфокусированное на свойствах данных, которые занимают конкретные пространственные масштабы. Эта способность может быть использована не только для анализа данных, но также и для их сжатия. Манипулируя вейвлет-преобразованием, компьютер «прищуривается» на изображение и отбрасывает нежелательные масштабы разрешения. Именно это решило сделать ФБР в 1993 году. В то время дактилоскопическая его база данных содержала 200 млн записей, которые хранились в виде чернильных отпечатков на бумажных карточках. В процессе модернизации эти изображения оцифровывались, а результаты закладывались в компьютер. Очевидным преимуществом новой системы была возможность быстро искать в базе соответствия отпечаткам, найденным на месте преступления.

Традиционное изображение с достаточным разрешением дает компьютерный файл объемом 10 Мб для каждой карточки с отпечатками. Архив ФБР занимает 2000 терабайт памяти. Каждый день в него поступает по крайней мере 30 000 новых карточек, так что требования к объему хранилища возрастают на 2,4 трлн двоичных цифр ежедневно. ФБР отчаянно нуждалось в сжатии данных. Там пробовали JPEG, но этот формат бесполезен для отпечатков пальцев (в отличие от отпускных фоток), когда коэффициент сжатия – отношение размера первоначальных данных к размеру сжатых – становится высоким, примерно 10:1. Тогда сжатые изображения теряют смысл из-за так называемых артефактов в виде квадратиков, в которых деление на блоки 8 × 8 оставляет заметные границы. Естественно, метод был практически бесполезен для ФБР, если не мог обеспечить сжатия по крайней мере 10:1. Артефакты-квадратики – это не просто эстетическая проблема: они серьезно ухудшают способность алгоритмов проверять отпечатки пальцев на соответствие. Альтернативные методы на основе преобразования Фурье также привносили в изображения нежелательные артефакты, причем все они связаны с проблемой бесконечных «хвостов» в синусах и косинусах рядов Фурье. Так что Том Хоппер из ФБР и Джонатан Брэдли с Крисом Брислоном из Лос-Аламосской национальной лаборатории решили кодировать оцифрованные записи с отпечатками пальцев при помощи вейвлетов с использованием метода, известного как вейвлет-скалярное квантование, или, короче, WSQ.

Вместо того чтобы удалять избыточную информацию путем создания артефактов-квадратиков, WSQ удаляет мелкие детали по всей площади изображения – детали настолько мелкие, что они не влияют на способность глаза распознавать структуру отпечатка пальца. В проведенных ФБР испытаниях все три опробованных вейвлет-метода показали себя лучше двух фурье-методов, таких как JPEG. В итоге самым разумным методом оказался WSQ. Он обеспечивает коэффициент сжатия не менее 15:1, снижая стоимость хранения информации на 93 %. Теперь WSQ является стандартом для обмена и хранения отпечатков пальцев. Большинство американских правоохранительных органов пользуются им для сжатия отпечатков пальцев с разрешением 500 dpi (пикселей на дюйм). Для отпечатков с более высоким разрешением они используют JPEG{60}.

Вейвлеты появляются практически везде. Команда Денниса Хили применяет основанные на вейвлетах методы коррекции изображений к результатам КТ, ПЭТ и МРТ-сканирования. Они также используют вейвлеты для доработки стратегий, посредством которых сканеры получают свои данные. Рональд Койфман и Виктор Викерхаузер использовали их для удаления нежелательного шума в записях. Настоящим триумфом стало восстановление записи исполнения Иоганнесом Брамсом одного из своих «Венгерских танцев», сделанной на восковом валике в 1889 году, хотя он и был частично оплавленным. Запись перевели на диск так, что она воспроизводилась на скорости 78 оборотов в минуту. Койфман начал с того, что передал запись по радио, хотя к тому моменту музыка там была уже почти неслышна на фоне шума. После вейвлетной очистки на записи уже можно было услышать, что играет Брамс, – не идеально, но все же услышать.

Отпечатки пальцев. Слева: оригинал. Справа: после сжатия до 1/26 объема данных

Лет 40 назад функциональный анализ был всего лишь еще одной мудреной областью абстрактной математики, которая если где и применялась, то разве что в теоретической физике. Появление вейвлетов все изменило. Теперь функциональный анализ обеспечивает базу, необходимую для разработки новых типов вейвлетов с особыми свойствами, которые делают их применимыми в прикладной физике и технике. Сегодня вейвлеты незаметно вошли практически во все аспекты нашей жизни – они используются в сфере профилактики преступности, в медицине, в цифровой музыке нового поколения. Завтра они захватят весь мир.