Это база: Зачем нужна математика в повседневной жизни

13 Позовите тополога

Топология – одна из гибких разновидностей геометрии – первоначально представляла собой в высшей степени абстрактную часть чистой математики. Большинство из тех, кто хотя бы слышал о ней, по-прежнему так считает, но ситуация потихоньку начинает меняться. То, что может существовать нечто под названием «прикладная топология», на первый взгляд кажется невероятным. Это как учить свинью петь: замечательным результатом было бы не то, что свинья поет хорошо, а уже то, что она вообще поет. Такая оценка справедлива в отношении свиней, но совершенно несправедлива в отношении топологии. Сегодня, в XXI веке, прикладная топология несется вперед на всех парах и решает важные задачи в реальном мире. На самом деле это незаметно происходит уже не первый день, но сейчас процесс достиг такой стадии, когда прикладную топологию уже можно вполне обоснованно считать новой отраслью прикладной математики. И речь идет не о случайных применениях каких-то аспектов топологии: ее применения едва ли не повсеместны, а используемые топологические инструменты охватывают значительную часть предмета, включая самые хитроумные и абстрактные моменты. Косы. Комплексы Вьеториса – Рипса. Векторные поля. Гомология. Когомология. Гомотопия. Теория Морса. Индекс Лефшеца. Расслоенные пространства. Пучки. Категории. Копределы.

На это есть причина: единство. Сама топология тоже выросла, всего за столетие с небольшим, из кучки небольших диковинок до полностью интегрированной области исследований и знаний. Сегодня это одна из главных опор, на которых зиждется вся математика. А везде, куда приходит чистая математика, появляется и прикладная математика. Со временем. (Обратный процесс тоже случается.)

Топология изучает, как изменяются фигуры под действием непрерывных преобразований и, в частности, какие свойства они при этом сохраняют. Знакомые примеры топологических структур – лента Мёбиуса, то есть односторонняя поверхность, и узлы. На протяжении почти 80 лет математики изучали топологию из природного любопытства и не думали ни о каком практическом применении. Предмет становился все более абстрактным, появлялись заумные алгебраические структуры, получившие название гомологии и когомологии, чтобы делать такие вещи, как подсчет числа отверстий в топологической фигуре. Все это казалось очень невразумительным и не имело значения для практики.

Однако математики не теряли присутствия духа и продолжали работать над топологией из-за ее центральной роли в развитом математическом мышлении. Компьютеры становились все более мощными, и математики начали искать способы электронного воплощения топологических концепций, которое позволило бы исследовать очень сложные формы. Но, чтобы компьютеры получили возможность производить нужные вычисления, исследователям пришлось изменить подход к вопросу. Результат, известный как «постоянная гомология», – это цифровой метод поиска отверстий.

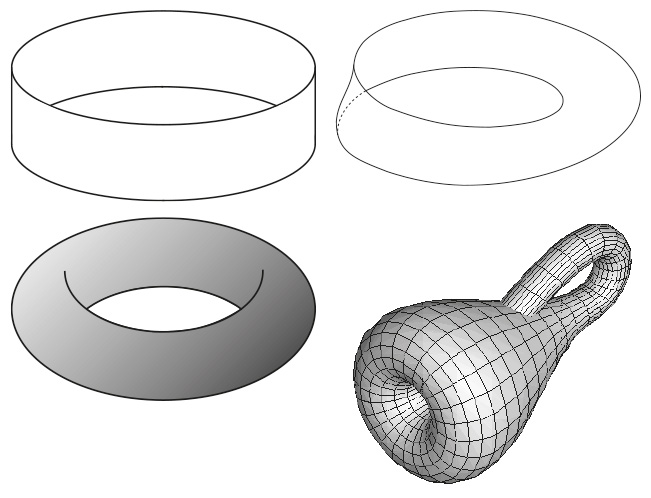
Вверху слева: цилиндр. Вверху справа: лента Мёбиуса.

Внизу слева: тор. Внизу справа: бутылка Клейна

На первый взгляд, задача распознавания отверстий кажется очень далекой от реального мира. Но топология оказывается идеальным средством для решения некоторых задач, связанных с сетями датчиков охранной сигнализации. Представьте себе секретное правительственное учреждение, окруженное лесом и неизменно привлекающее к себе внимание террористов и воров. Чтобы вовремя заметить их приближение, вы размещаете в лесу датчики движения. Как эффективнее всего это сделать и как убедиться, что в кордоне нет дыр, через которые плохие парни смогут пройти незамеченными?

Дыры? То есть отверстия? Конечно! Зовите тополога.

Когда вы впервые знакомитесь с топологией, вам обычно рассказывают о базовых формах. Они кажутся очень простыми и странными маленькими игрушками. Одни из них причудливы, другие откровенно жутковаты. Но эти причуды имеют смысл. Как однажды сказал великий математик Гильберт, «искусство математики состоит в нахождении того частного случая, который содержит все зародыши общности». Стоит выбрать правильную игрушку, и перед вами откроются совершенно неизведанные области.

Первые две игрушки на рисунке можно сделать, взяв полоску бумаги и соединив ее концы. Очевидный способ сделать это дает нам цилиндрическую полоску. Менее очевидный состоит в предварительном перекручивании одного конца на 180°. Это лента Мёбиуса, названная в честь Августа Мёбиуса, наткнувшегося на такую забавную штуку в 1858 году, хотя еще до этого ее заметил ученик Гаусса Иоганн Листинг. Именно Листинг в 1847 году первым пустил в оборот название «топология», но прозорливо подталкивал его к этому зарождающемуся предмету с самого начала не кто иной, как Гаусс.

У цилиндра имеются два края, каждый из которых представляет собой окружность, и две стороны, или поверхности. Можно раскрасить цилиндр внутри в красный цвет, а снаружи в синий, и эти два цвета нигде не встретятся. В топологии значение имеют те свойства фигур, которые сохраняются при непрерывной деформации фигуры. Вы можете растягивать ее части, сжимать их или скручивать, но не имеете права разрезать или рвать – разве что позже соедините все как было. Одинаковая всюду ширина цилиндрической ленты на рисунке не является ее топологическим свойством: ширину можно изменить путем непрерывной деформации. Округлость краев тоже не топологическое свойство, по аналогичным причинам. Но само наличие двух краев и двух сторон – топологические свойства.

Фигуры, которые считаются идентичными при деформации, имеют особое название: мы называем их топологическими пространствами. Настоящее определение звучит в высшей степени абстрактно и заумно, так что я буду пользоваться более неформальными изобразительными средствами. Однако все, что я говорю, может быть сформулировано точно и надлежащим образом доказано.

Мы можем использовать эти топологические свойства для доказательства того, что цилиндр невозможно непрерывной деформацией превратить в ленту Мёбиуса. Хотя то и другое получается в результате склеивания концов бумажной полоски, это разные топологические пространства. Причина в том, что у ленты Мёбиуса всего один край и одна сторона. Если провести по краю бумажной ленты пальцем, то палец сделает два оборота, прежде чем вернется в исходную точку. При этом он благодаря перекручиванию на 180° перейдет сверху вниз и обратно. Если вы начнете закрашивать поверхность красной краской, то сделаете полный оборот и обнаружите, что закрашиваете оборот той части бумаги, которую уже окрасили, опять же благодаря перекручиванию на 180°. Так что лента Мёбиуса имеет другие топологические свойства по сравнению с цилиндром.

Фигура внизу слева похожа на бублик. Математики называют такую фигуру тором, имея в виду только поверхность, но не внутреннюю часть, где у бублика находится мякиш. В этом тор больше напоминает надувной спасательный круг. В нем есть отверстие. Вы можете просунуть в это отверстие палец или, в случае спасательного круга, тело. Но это отверстие не в самой поверхности. Если бы это было так, надувной спасательный круг сдулся бы – и вы бы утонули. Отверстие расположено в месте, где поверхности как раз нет. Это совершенно логично: инженер широкополосной связи, сидящий в инспекционном люке, тоже находится там, где нет поверхности. Но у люка есть края, а вот у тора имеется отверстие, но нет ни одного края. Как и у цилиндра, у тора две стороны: та, что мы видим на рисунке, и та, что «внутри».

Фигура внизу справа менее известна. Это бутылка Клейна. Она называется так в честь великого немецкого математика Феликса Клейна и потому, что внешне похожа на бутылку. Название, по-видимому, было немецким каламбуром, поскольку по-немецки Fläche означает «поверхность», а Flasche – «бутылка». В одном отношении рисунок выглядит обманчиво: кажется, что поверхность протыкает себя насквозь. В бутылке Клейна такого не происходит. Самопересечение возникает потому, что мы, естественно, рисуем так, будто предмет находится в трехмерном пространстве. Чтобы получить бутылку Клейна без самопересечений, нужно либо выйти в четыре измерения, либо, что еще лучше, последовать стандартной топологической практике – вообще отбросить потребность в окружающем пространстве. Тогда бутылку Клейна можно рассматривать как цилиндр, два круглых конца которого соединены друг с другом, но после того, как один из них вывернули наизнанку. Чтобы проделать это в трехмерном пространстве, необходимо проткнуть концом цилиндра его стенку и вновь его там раскрыть, но можно сделать то же самое концептуально, просто добавив правило, по которому вы, падая с одного конца цилиндра, оказываетесь на другом его конце, со сменой направления вдоль окружности. У бутылки Клейна, как у тора, нет краев, а ленту Мёбиуса она напоминает тем, что имеет только одну сторону.

Итак, мы описали различия всех четырех приведенных на рисунке топологических пространств. Они различаются либо числом концов, либо числом сторон. Либо типами отверстий, если мы только сможем сказать, что подразумеваем под отверстием. Это наблюдение открывает один из фундаментальных вопросов топологии. Как определить, являются ли данные топологические пространства идентичными или отличаются друг от друга? Для этого недостаточно просто посмотреть на фигуру, потому что она может быть деформирована. Как говорится, для тополога что бублик, что кофейная чашка – все едино. Чтобы ответить на вопрос, необходимо привлечь топологические свойства, по которым различаются пространства.

Сделать это не всегда просто.

Бутылка Клейна выглядит как классическая математическая игрушка. Трудно понять, как она может, хотя бы в принципе, быть полезной в реальном мире. Конечно, Гильберт настаивал, что математические игрушки ценны не сами по себе, а через теории, на создание которых они вдохновляют, так что бутылке Клейна нет нужды оправдывать свое существование непосредственно. На самом деле эту невероятную фигуру все же можно отыскать в природе. Она возникает в зрительной системе приматов – а это обезьяны обычные и человекообразные, ну и, конечно, мы.

Более столетия назад невролог Джон Хьюлингс Джексон выяснил, что кора головного мозга человека содержит своеобразную топографическую карту мышц тела. Кора – это извилистая поверхность мозга, так что все мы держим в голове карту собственных мышц. Это полезно, потому что мозг управляет сокращением и расслаблением мышц и, соответственно, нашими движениями. Значительная часть коры отвечает за зрение, и мы сегодня знаем, что зрительная кора содержит в себе аналогичные карты, управляющие зрительным процессом.

Зрение – это не только глаз, работающий как камера и посылающий фотографию в мозг. Оно намного сложнее, потому что мозг должен не только получить изображение, но и распознать его. Подобно камере, глаз имеет линзу для фокусировки входящего изображения, а работа сетчатки немного напоминает работу пленки. На самом деле зрительный процесс ближе к работе цифровых камер. Свет попадает на крохотные рецепторы на сетчатке, именуемые палочками и колбочками, а нейронные связи передают сигналы в кору мозга по зрительному нерву – пучку нервных волокон. По пути эти сигналы обрабатываются, но основную часть анализа берет на себя кора.

Зрительную кору можно представить в виде ряда слоев, уложенных друг на друга. У каждого слоя своя роль. Верхний слой V1 распознает границы между частями изображения. Это первый шаг сегментирования сигнала на составляющие части. Информация о границах передается глубже в кору и на каждом шаге анализируется на наличие следующего типа структурной информации, а затем преобразуется для передачи на следующий уровень. Естественно, это сильно упрощенное описание, да и «слои» – тоже упрощение. На самом деле много сигналов передается и в обратном направлении. Эта система создает в наших головах многоцветное трехмерное представление внешнего мира – настолько живое и подробное, что по умолчанию мы считаем, что это и есть окружающий мир. Это не совсем соответствует истине, что и демонстрируют наглядно зрительные иллюзии и двусмысленности. Во всяком случае, в конечном итоге кора сегментирует изображение на части, в которых мы можем узнать кошку, или тетю Веру, или что угодно еще. А затем мозг может вызвать дополнительную информацию: кличку кошки или тот факт, что Вера недавно выиграла в лотерею.

Слой V1 распознает границы при помощи островков нервных клеток, чувствительных к краям, ориентированным в тех или иных направлениях. На рисунке показана часть V1, полученная путем оптической записи из зрительной коры макаки. Разные оттенки серого (в статье, послужившей мне источником, их называют цветами, так что и я буду их так называть) соответствуют нейронам, которые срабатывают при получении данных, указывающих на границу такой ориентации. Цвет непрерывно переходит от одного оттенка к другому, за исключением отдельных изолированных точек, где все цвета существуют рядом в конфигурации, напоминающей колесо со спицами. Эти точки представляют собой сингулярности поля ориентации.

Эта конфигурация ограничена топологическими свойствами поля ориентации. Существует всего два способа расположить серию цветов вокруг сингулярности так, чтобы все переходы были непрерывны: цвета будут меняться либо последовательно по часовой стрелке, либо против. На рисунке показаны примеры обоих вариантов. Присутствие сингулярностей неизбежно, поскольку зрительной коре, чтобы распознать линию целиком, приходится использовать много вертушек – поворотных пунктов.

Теперь мы зададимся вопросом, как мозг совмещает информацию об ориентации с информацией о том, как граница движется. Направление – это не только прямая, но и стрелочка на ней (север противолежит югу, хотя то и другое находится на одной прямой), и после поворота на 180° стрелочка меняется на противоположную. Чтобы направление вернулось к первоначальному, необходимо совершить поворот на 360°. Границы не имеют стрелочек и потому возвращаются к первоначальному состоянию после поворота на 180°. Кора должна каким-то образом обеспечить работу и направлений, и границ одновременно. Если обвести сингулярность петлей, ориентации вокруг петли будут меняться непрерывно, но поле направлений должно будет перевернуться с заданного направления на противоположное – скажем, с северного на южное – нечетное число раз. Эти утверждения по природе своей топологичны, и они привели ученого по имени Сигеру Танака к выводу о том, что рецептивные поля связаны друг с другом с топологией бутылки Клейна{66}. Это предсказание уже проверено экспериментально на разных животных, в том числе на мартышках, кошках и хорьках, и полученные данные указывают на то, что организация зрительной коры у многих млекопитающих схожа. С людьми эксперименты не проводились по этическим соображениям, но мы тоже млекопитающие, более того – приматы. Поэтому вполне вероятно, что у нас, как и у макак, в голове имеются бутылки Клейна, помогающие нам воспринимать движущиеся объекты.

Цвета (здесь оттенки серого) показывают ориентацию, которая порождает больше всего активности в каждом участке коры. Воспринимаемая ориентация меняется плавно, за исключением точек сингулярности, где все цвета сходятся[12]

Эти идеи интересны не только биологам. В стремительно развивающейся области биомиметики инженеры учатся у природы, что позволяет им создавать новые материалы и новые машины. Например, в изобретении рентгеновских телескопов важнейшую роль сыграла любопытная структура глаза омара{67}. Чтобы сфокусировать пучок рентгеновских лучей, необходимо изменить их направление, но у них настолько высокая энергия, что подходящее зеркало может отклонить луч только на очень небольшой угол. Эволюция омара решила аналогичную проблему для видимого света миллионы лет назад, и эта же геометрия работает для рентгеновских лучей. Новые представления о слое V1 коры головного мозга у млекопитающих могут быть перенесены и на компьютерное зрение, с потенциальным применением в таких сферах, как беспилотные автомобили и машинная интерпретация спутниковых снимков для военных и гражданских целей.

Центральный вопрос топологии звучит так: «Какая это фигура?» То есть «Какое топологическое пространство мы здесь видим?» Вопрос может показаться банальным, но математика представляет нам топологические пространства самыми разными способами – в виде картинок, формул, решений уравнений, поэтому не всегда понятно, что мы получаем. Например, только тополог способен разглядеть бутылку Клейна в слое V1 мозга макаки. Мы замахнулись на решение этой задачи, когда заметили, что четыре пространства на моем рисунке – цилиндр, лента Мёбиуса, тор и бутылка Клейна – различаются топологическими свойствами. Ближе к концу XIX века и в начале XX века математики разработали систематические подходы к этому вопросу. Ключевая идея состоит в том, чтобы определить топологические инварианты – свойства, которые можно вычислить и которые одинаковы у топологически эквивалентных пространств, но различны по крайней мере у некоторых неэквивалентных пространств. Обычно этого недостаточно, чтобы различать все неэквивалентные пространства, но даже частичная классификация полезна. Если у двух пространств различается какой-то из инвариантов, то эти пространства определенно имеют различную топологию. При рассмотрении четырех фигур, о которых мы говорили, инвариантами являются такие аспекты, как «сколько краев?» и «сколько сторон?».

За прошедшие десятилетия выяснилось, что одни инварианты полезнее других, и было построено несколько инвариантов, имеющих фундаментальное значение. Тот, о котором я хочу сейчас рассказать (отчасти потому, что в последнее время у него появились серьезные сферы применения), называется гомологией. По существу, он подсчитывает, сколько отверстий заданной размерности имеет пространство. Мало того, он не просто подсчитывает: он соединяет отверстия и неотверстия в единый алгебраический объект, называемый группой гомологий.

Есть одно базовое топологическое пространство, которое я до сих пор не упоминал: сфера. Как и в случае с тором, когда математики произносят это слово, они подразумевают бесконечно тонкую поверхность, а не заполненную сферу (которую называют шаром). У сферы нет краев, как у тора и бутылки Клейна. Мы можем показать, что она топологически отличается и от тора, и от бутылки Клейна, если посмотрим на отверстия или их отсутствие.

Начнем с тора. С первого взгляда очевидно, что у тора прямо в середине есть огромное и очень заметное отверстие. Сферы выглядят совершенно иначе. Но как определить отверстие математически, так, чтобы определение не зависело от окружающего пространства? Ответ в том, что смотреть надо на замкнутые кривые на поверхности. Любая замкнутая поверхность на сфере образует границу области, которая с топологической точки зрения представляет собой диск – внутренность окружности{68}. Доказательство этого довольно заковыристо, поэтому будем просто считать, что так оно и есть. На торе некоторые замкнутые кривые также ограничивают диски, но некоторые нет. Мало того, любая замкнутая кривая, проходящая «сквозь» отверстие, не может ограничивать диск. Доказать это тоже довольно непросто, но мы опять смиримся с судьбой и будем считать, что все в порядке. Таким образом, мы показали, что сфера топологически отличается от тора, потому что «замкнутая кривая» и «ограничивает (топологический) диск» – это топологические свойства.

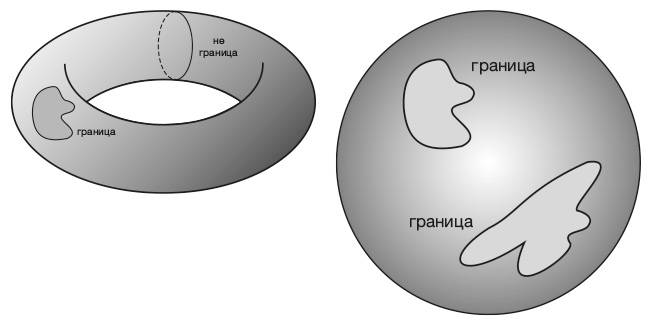
Слева: на торе некоторые замкнутые кривые являются границами, а некоторые нет. Справа: на сфере все замкнутые кривые являются границами

В эту игру можно играть и при более высоких размерностях. Например, в трех измерениях можно заменить «замкнутую кривую» на «(топологически) сферическую поверхность», а «ограничивает диск» на «ограничивает шар». Если вы сумеете найти сферу, которая не ограничивает шар, это будет означать, что в пространстве имеется трехмерное отверстие. Если вы хотите пойти дальше и определить это отверстие, то знайте, что еще первые топологи обнаружили возможность складывать и вычитать замкнутые кривые, или сферы. Я расскажу, как это происходит с кривыми на поверхностях, для более высоких размерностей все аналогично, но более хлопотно.

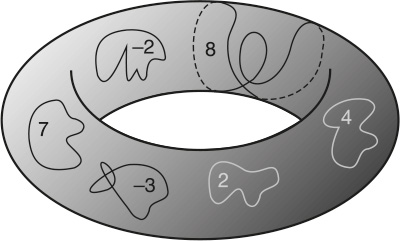
Цикл на торе

По существу, вы складываете две замкнутые кривые, когда рисуете их на одной поверхности. Чтобы сложить целое множество кривых, следует нарисовать их все. Существуют, правда, технические тонкости: часто полезно бывает рисовать вдоль кривой стрелочку, обозначая ее ориентацию, а одну и ту же кривую можно рисовать много раз и даже отрицательное число раз. Это почти то же самое, что рисовать обратную ей кривую (та же кривая, противоположная ориентация) положительное число раз, в смысле, который я скоро объясню.

Множество кривых, помеченных числами, которые показывают, сколько раз нужно нарисовать каждую из них, называется циклом. На поверхности существует бесконечное число возможных циклов, но топологически многие из них эквивалентны друг другу. Итак, я только что сказал, что минус цикл – это тот же цикл, где все стрелочки перевернуты. На самом деле это не совсем верно, потому что «тот же» означает «идентичный», а циклы эти не идентичны. Но мы можем сделать их одинаковыми, применив топологический вариант фокуса, который проделывают специалисты по теории чисел в модулярной арифметике. Там, хотя числа 0 и 5 не одинаковы, мы можем сделать вид, что они одинаковы для определенных целей, и получить кольцо Z₅ целых чисел по модулю 5. В теории гомологий мы проделываем фокус того же рода и делаем вид, что любая замкнутая кривая, которая ограничивает диск, – то же самое, что нулевая кривая, и не рисуем ни одной ее копии. Такую кривую называют границей и говорят, что она гомологична нулю. Эта же идея распространяется и на циклы: цикл гомологичен нулю, если представляет собой комбинацию кривых, каждая из которых является границей.

Мы можем сложить циклы C и D и получить C + D, как уже описывалось, а можем вычесть один из другого, перевернув стрелочки в цикле D, и получить C – D; правда, C – С не обязательно должно равняться 0. Это раздражает, но выход есть: эта разность всегда гомологична нулю. Если мы сделаем вид, что все гомологичное нулю равно нулю, то получим прекрасный алгебраический объект, называемый группой гомологий на поверхности. В результате мы производим алгебраические операции над циклами по модулю (то есть игнорируя) границ. Точно так же, как мы занимаемся арифметикой (mod 5), игнорируя числа, кратные 5.

Это и есть гомология.

Группа гомологий сферы тривиальна: каждый цикл гомологичен нулю и группа состоит только из одного 0. Группа гомологий тора не тривиальна: некоторые циклы в ней не гомологичны нулю. Оказывается, каждый цикл гомологичен целому кратному цикла, обозначенного на рисунке как «не граница», так что группа гомологий тора представляет собой замаскированное множество целых чисел Z. Я не буду ничего считать и рисовать диаграммы, но группа гомологий бутылки Клейна – это Z₂ × Z₂, пары (m, n) целых чисел по модулю 2. Так что у бутылки тоже имеется отверстие, но это отверстие иного рода, чем отверстие в торе (ну, не совсем в нем).

Я рассказал вам о довольно сложной конструкции – группе гомологий – не без причины: мне хотелось дать вам представление о том, как топологи строят инварианты. Но единственное, что вам следует вынести отсюда, – это мысль о том, что у каждого пространства имеется группа гомологий, что это топологический инвариант и что с его помощью можно многое выяснить о форме пространства. В топологическом смысле.

Понятие группы гомологий восходит к новаторским исследованиям Энрико Бетти и Пуанкаре, проводившимся в конце XIX века. Их подход состоял в подсчете топологических особенностей, таких как отверстия, но в конце 1920-х годов он был переведен на язык теории групп стараниями Леопольда Вьеториса, Вальтера Майера и Эмми Нётер, а вскоре появились и широкие обобщения. То, что я называю просто группой гомологий, – это всего лишь первая из целого ряда таких групп, определяющих алгебраическую структуру отверстий размерности 1, 2, 3 и т. д. Существует также парное понятие когомологии и родственное понятие гомотопии, связанное скорее с тем, как кривые трансформируются и соединяются конец к концу, а не с тем, какое отношение они имеют к границам. Пуанкаре понимал, что эта конструкция дает группу, в которой, как правило, не выполняется перестановочный закон. Сегодня алгебраическая топология – это громадная узкоспециализированная область, где продолжают открывать новые топологические инварианты.

Существует также стремительно растущая область, известная как прикладная топология. Поскольку новое поколение математиков и физиков знакомо с топологией практически с детства, для них она оказывается куда менее странной и пугающей, чем была в свое время для старшего поколения. Они бегло говорят на языке топологии и видят новые возможности применения ее для решения практических задач. Бутылка Клейна в зрительной системе – пример с передовых позиций биологии. В материаловедении и радиоэлектронике можно найти такие понятия, как топологические изоляторы: это материалы, которые можно переводить из проводящего состояния в непроводящее, меняя топологию их электрических свойств. Топологические качества, сохраняющиеся при деформациях, очень стабильны.

Одна из наиболее перспективных концепций прикладной топологии возникла, когда специалисты по чистой математике пытались написать алгоритмы, которые позволили бы компьютеру вычислять группы гомологий. Им удалось это сделать, переписав определение группы гомологий так, чтобы оно больше подходило для компьютерных вычислений. Впоследствии эти идеи оказались эффективным новым методом анализа «больших данных». При этом чрезвычайно модном подходе ко всем областям науки компьютеры используются для поиска скрытых закономерностей в численных данных. Как явствует из названия, он работает лучше всего с очень большими объемами данных. К счастью, современные датчики и электроника чрезвычайно хорошо умеют измерять, хранить и манипулировать гигантскими объемами данных. К несчастью, мы часто понятия не имеем, что делать с этими данными после того, как собрали их, но именно здесь и кроются математические загадки больших данных.

Предположим, вы наизмеряли миллионы чисел и принципиально представляете их как своего рода облако точек в многомерном пространстве переменных. Чтобы извлечь из этого облака данных осмысленные закономерности, необходимо найти выраженные структурные особенности. Первостепенна среди них форма облака. Ее невозможно определить, просто нанеся точки на экран и посмотрев на них, – может оказаться, что вы смотрите не с того направления, или важные группы точек затенены другими точками, или число переменных слишком велико, чтобы зрительная система нормально их обрабатывала. Но, как мы уже видели, «Какой это формы?» – фундаментальный вопрос в топологии. Поэтому резонно предположить, что топологические методы могут помочь отличить, скажем, примерно сферическое облако данных от тороидального с отверстием в нем. Что-то отдаленно похожее на это мы делали для проекта FRACMAT из главы 8. Там важно было, насколько компактно облако точек и является ли оно округлым или вытянутым. Более тонкие топологические детали значения не имели.

Невозможно разобраться в топологии миллиона точек данных вручную: необходимо использовать компьютер. Но компьютеры сконструированы не для того, чтобы анализировать топологию. Так что методы, которые специалисты по чистой математике разрабатывали для компьютерных расчетов групп гомологий, были перенесены в область больших данных. И, как всегда, в готовом виде они не делали работу полностью. Их нужно было адаптировать к новым требованиям больших данных, главное из которых – то, что форма облака данных не является четко определенной. Она зависит, в частности, от масштаба, в котором вы рассматриваете облако.

Представьте, например, шланг, уложенный в бухту. При взгляде с умеренного расстояния сегмент шланга похож на кривую, которая топологически есть одномерный объект. Вблизи он похож на длинную цилиндрическую поверхность. Еще ближе поверхность обретает толщину, более того, вдоль середины цилиндра проходит отверстие. Если отойти и посмотреть издалека, но под широким углом, шланг окажется свернутым как сжатая пружина. А стоит расфокусировать зрение, бухта расплывется в… тор.

Подобного рода эффект означает, что форма облака данных – не постоянное понятие. Так что группа гомологий тоже не такая уж замечательная идея. Вместо этого математики задаются вопросом о том, как воспринимаемая топология облака данных меняется с масштабом наблюдения.

Соединение точек данных, разделенных различными расстояниями, создает ряд триангуляций и вскрывает отверстия разных размеров. Постоянная гомология распознает эти эффекты

Начиная с облака и выбранной мерки длины, вы можете создать то, что топологи называют симплексным комплексом. Для этого следует соединить точки попарно ребрами везде, где они оказываются ближе друг к другу, чем предписывает выбранная мерка. Тогда ребра, которые находятся близко друг к другу, окружают треугольники, а треугольники, которые находятся близко друг к другу, окружают тетраэдры и т. д. Многомерный тетраэдр называется симплексом, а набор симплексов, объединенных определенным образом, есть симплексный комплекс. Для нас подойдет и более простое его название «триангуляция». Помните только, что треугольники могут быть любой размерности.

Если у вас есть триангуляция, существуют математические правила вычисления гомологии. Но ведь триангуляция зависит от масштаба наблюдения. Так что и гомология тоже от него зависит. Наш интересный вопрос о форме тогда приобретает вид: как меняется гомология триангуляции с изменением масштаба? Важнейшие особенности формы должны быть менее подвержены изменениям, нежели более неустойчивые черты, которые чувствительны к масштабу. Так что мы можем сосредоточиться на тех аспектах группы гомологий, которые сохраняются при изменениях масштаба. Результирующий инструмент – не просто группа гомологий, а семейство таких групп, по одной на каждый масштаб, – известен как постоянная гомология.

Здесь последовательность из шести рисунков показывает, какие точки соединяются на разных масштабах, при разных мерках длины. С увеличением мерки – а мы при этом видим все более грубые структуры – в начальном облаке отдельных точек начинают формироваться небольшие сгустки, в одном из которых мы видим столь же небольшое отверстие. Это отверстие заполняется, а сгустки растут. Затем сгустки объединяются в кольцо, открывая нашему взору большое отверстие. Его стенки постепенно утолщаются, но само оно остается большим отверстием, пока мерка длины не станет такой большой, что все заполнится целиком. Рисунок схематичен, а подробности, которые добавил бы компьютерный алгоритм, опущены для ясности. Доминантной чертой, существующей на максимальном диапазоне шкал, является большое отверстие в середине.

Штрихкод постоянной гомологии показывает, какие структуры сохраняются на каких масштабах. (Схематично.)

Обратите внимание, что это описание включает в себя не только топологию, но и информацию о расстоянии. Формально топологическое преобразование не обязано сохранять расстояния, но в анализе данных их реальные значения важны не менее, чем общая топологическая форма. Поэтому постоянная гомология обращает внимание не только на топологические, но и на метрические свойства. Один из способов представления информации, полученной при помощи постоянной гомологии, предполагает построение штрихкода, где горизонтальные линии обозначают диапазон масштабов, на которых сохраняются те или иные гомологические черты (такие как отверстия). Например, штрихкод для представленного на рисунке облака точек мог бы выглядеть примерно как штрихкод на рисунке выше. В штрихкоде схематически обобщается информация о том, как топология меняется с масштабом.

Постоянная гомология и ее штрихкоды – все это прекрасно, но для чего они могут пригодиться?

Представьте, что вы управляете бизнесом и ваши офисы располагаются на поляне в лесу. Грабители могут подойти к ним по лесу незамеченными. Поэтому вы устанавливаете вокруг датчики, каждый из которых способен регистрировать движение и поддерживать связь с соседними датчиками, и включаете эту систему по ночам. При появлении кого бы то ни было, законном или нет, датчики должны поднять тревогу, и тогда ваша служба безопасности может пойти на место и выяснить, в чем дело. Или представьте, что вы генерал и управляете военной базой в местности, где активно действуют террористические группы. Вы делаете что-то похожее, только с оружием.

Как гарантировать, что покрытие территории датчиками достаточно, что нет прорех, через которые преступник или террорист мог бы прокрасться внутрь?

Если датчиков немного, вы можете нанести их на карту и визуально оценить распределение. Если число датчиков велико или имеются различные ограничения, обусловленные рельефом местности, то такой метод становится менее реальным. Поэтому нужен способ обнаружения прорех в зоне действия датчиков… Искать прорехи? Похоже, это задача как раз для постоянной гомологии. В самом деле, это одна из тех многочисленных областей, где в настоящее время применяется эта новая идея. Аналогичное применение можно назвать «барьерным покрытием»: определить, защищает ли данный набор датчиков охраняемое здание или комплекс полностью. «Прочесывающее покрытие» относится к подвижным датчикам, а домашний, или коммерческий, вариант этого алгоритма используется в роботах-пылесосах. Весь ли пол он почистит?

Более научное применение метода реализуется совместно с методом скользящего окна для восстановления динамических аттракторов, который я упоминал в главе 8. Постоянная гомология может распознать момент, когда топология аттрактора существенно меняется. В теории динамических систем этот момент называют точкой бифуркации, он свидетельствует о серьезном изменении в динамике. Еще одно важное применение – выяснение того, как менялся климат Земли за миллионы лет, от теплых периодов к оледенениям и даже к полностью покрытой снегом и льдом Земле. Джесси Бервальд с коллегами показал, что штрихкоды облаков данных скользящего окна прекрасно помогают распознавать изменения в общем климатическом режиме{69}. Тот же метод применяется и к другим физическим системам, например в случае вибрации в станках. Фирас Хасавнех и Элизабет Манч выяснили, что временная серия измерения режущего инструмента может уловить эти вибрации, известные среди профессионалов как «дрожь»{70}. Кроме того, метод применяется и в медицинском сканировании, например для распознавания бифонирования при видеоэндоскопии гортани, которой занимаются Кристофер Трали и Хосе Переа{71}. Этот эффект возникает, когда голосовая связка производит звук сразу двух частот, и может указывать на повреждение или паралич связки. При эндоскопии гортани камера на конце оптоволоконного кабеля вводится в нос и опускается в горло. Саба Эмрани и другие{72} применили штрихкоды к аудиоданным, чтобы распознавать у пациентов свистящее дыхание – ненормальный высокий звук, который может указывать на частичную блокировку дыхательных путей или легочные заболевания, такие как астма, рак легких и хроническая сердечная недостаточность.

У вас проблемы с данными? Нужна срочная помощь?

Зовите тополога.