Это база: Зачем нужна математика в повседневной жизни

7 Папа, ты научился перемножать триплеты?

Деревня имеет средневековый вид, дома в ней крыты тростником, по грязной дороге катятся запряженные лошадьми повозки, вокруг виднеются засеянные поля и пасущиеся овцы. Узкая лента реки тянется меж тесно стоящих домиков, посверкивая золотом в свете заходящего солнца. Мы видим эту сцену сверху, как будто с самолета – когда самолет закладывает вираж или покачивает крыльями, вид тоже поворачивается и раскачивается. Но это не самолет: на экране появляются новые кадры – теперь это вид с земли, откуда просматривается силуэт дракона. Он приближается. Снова смена плана, мы видим пейзаж глазами дракона, который пикирует, скользит над крышами, изрыгает пламя, пересохший тростник вспыхивает…

Это может быть кино или компьютерная игра – в наше время то и другое порой трудно отличить друг от друга. В любом случае это триумф сгенерированной компьютером графики – CGI.

Математика ли это?

О да!

Должно быть, это какая-то новая математика.

Не слишком. Такое применение для нее действительно является новым, да и сама математика здесь в какой-то мере новая и хитроумная, но в той части, которую я имею в виду, ей уже около 175 лет. И эта часть математики раньше не предназначалась для компьютерной графики. Да и компьютеров тогда не было.

А предназначалась она для работы с более общей проблемой, не имеющей отношения к «железу»: с геометрией в трехмерном пространстве. С сегодняшней точки зрения потенциальная связь этой области с компьютерной графикой очевидна. Но она была похожа не на геометрию, а скорее на алгебру. Если, конечно, не считать, что она нарушает одно из базовых алгебраических правил. Придумал ее ирландский математический гений сэр Уильям Роуэн Гамильтон, который назвал свое изобретение кватернионами. По иронии судьбы кватернионы оказались не совсем тем, что он искал, и это было не случайно.

Того, что он искал, попросту не существовало.

Сегодня на нашей планете компьютеров больше, чем людей. Как известно, представителей рода человеческого насчитывается 7,6 млрд. А одних только ноутбуков на Земле больше 2 млрд, а еще существует почти 9 млрд смартфонов и планшетов, причем те и другие часто обладают большей вычислительной мощностью, чем лучший суперкомпьютер, который можно было купить в 1980 году{52}. А если учесть еще крохотные компьютеры, которые производители массово втискивают в посудомоечные машины, в тостеры, холодильники, стиральные машины и дверцы для кошки, то количество компьютеров превысит численность людей вчетверо.

Сейчас трудно представить, что так было не всегда. Инновационные изменения носят взрывной характер. Первые домашние компьютеры – Apple II, TRS-80, Commodore PET – появились на потребительском рынке в 1977 году, то есть больше 40 лет назад. Почти с самого начала одной из главных сфер применения домашних компьютеров стали игры. Графика была примитивной, игры очень простыми.

По мере того как компьютеры становились все быстрее, память росла, а цены падали, качество картинок росло, и компьютерная графика начала завоевывать киноиндустрию. Первым полнометражным анимационным фильмом, целиком сделанным на компьютере, стала «История игрушек» в 1995 году, хотя более короткие ролики начали появляться десятилетием раньше. К сегодняшнему дню спецэффекты стали сверхреалистичными и используются так широко, что мы едва их замечаем. Когда Питер Джексон снимал трилогию «Властелин колец», он не беспокоился об освещении вообще: с ним разбирались после, при последующей компьютерной обработке.

Мы настолько привыкли к высококачественной, быстро движущейся графике, что редко задумываемся, откуда это все взялось. Когда появилась первая видеоигра? За 30 лет до того, как мир увидел первые домашние компьютеры. В 1947 году пионеры телевидения Томас Голдсмит – младший и Эстл Рэй Манн оформили патент на «развлекательное устройство на основе катодно-лучевой трубки». Катодно-лучевая трубка – это короткая толстая стеклянная бутылка с широким, слегка выпуклым основанием – экраном – и узкой горловиной. Устройство в горловине бомбардирует экран потоком электронов, а электромагниты изменяют направление этого потока так, что он делает на экране последовательные горизонтальные проходы, подобно движению человеческого глаза при чтении текста. Электронный луч, попадая на переднюю часть трубки, вызывает свечение специального покрытия и создает яркую точку. В большинстве телевизоров для создания изображения использовались именно катодно-лучевые трубки (еще их называют электронно-лучевыми), пока в 1997 году на рынке не появились телевизоры с плоским экраном. Игра Голдсмита и Манна родилась под впечатлением от радарных дисплеев Второй мировой войны. Световая точка представляла летящую ракету, а игрок пытался заставить ее попасть в цель, которую рисовали на бумаге и прикрепляли к экрану.

К 1952 году большая вычислительная машина EDSAC одолела головокружительные высоты игры в крестики-нолики. Хитом у пользователей стала игра Pong – одна из первых диалоговых видеоигр компании Atari – упрощенная двумерная игра в настольный теннис с шариком, отскакивавшим от двух ракеток, каждой из которых управлял один игрок. По сегодняшним меркам графика там была очень примитивной – ракетки изображали два подвижных прямоугольника, а шарик – маленький квадратик. Действие в этой игре почти отсутствовало, но до появления более совершенных технологий она была заметным достижением.

Вряд ли надо говорить, что Гамильтон не мог даже вообразить подобное применение для своего математического детища. Чтобы созреть и прорасти, этой идее потребовалось 142 года. Но задним числом мы понимаем, что эта возможность изначально присуща тому типу задач, на решение которых было нацелено его открытие. В математике существует множество стилей. Математики могут заниматься решением задач и искать ответы на конкретные вопросы, будь то в реальной жизни или в высоком мире чистой математики. Они могут посвящать себя построению теорий и заниматься доказательством бесчисленных специализированных теорем в рамках единой системы. Среди них могут встречаться талантливые одиночки, перескакивающие с одной области на другую и работающие над тем, что захватило их воображение. Они могут быть и инструментальщиками, разрабатывающими новые инструменты, пригодные для решения пока не поставленных вопросов, и методы, пока не нашедшие применения.

Гамильтон известен в основном как создатель теорий, но кватернионы – достойный пример его мастерства как инструментальщика. Он придумал их, чтобы обеспечить алгебраическую структуру для системных расчетов в области геометрии трехмерного пространства.

Гамильтон родился в Дублине (Ирландия) в 1805 году и был в семье четвертым ребенком из девяти. Его матерью была Сара Хаттон, а отцом – Арчибальд Гамильтон, стряпчий. В три года Уильяма отправили жить к его дяде Джеймсу, который управлял школой. У Уильяма не по годам рано проявился талант к языкам, но он сумел самостоятельно освоить и математику. Именно математику он изучал позже, с 18 лет, в дублинском Тринити-колледже и получал самые высокие оценки. Джон Бринкли, епископ Клойнский, выразился так: «Этот молодой человек, я не говорю станет, он уже является первым математиком своего поколения». Епископ, похоже, был прав, и в 1837 году, будучи еще студентом, Гамильтон стал эндрюсским профессором астрономии и королевским астрономом Ирландии. Оставшуюся часть своей профессиональной жизни он провел в Дансинкской обсерватории близ Дублина.

Самые известные его работы посвящены оптике и динамике, в первую очередь замечательной связи между двумя этими очень разными областями математической физики. Гамильтон переформулировал их с точки зрения общей математической концепции – основной функции. Сегодня мы называем эту функцию гамильтонианом и понимаем, что она привела к крупным успехам в обеих областях. Позже она оказалась именно тем, что нужно было для совершенно новой и очень странной теории – квантовой механики.

Мы уже упоминали Гамильтона в предыдущей главе. В 1833 году он сумел найти решение не поддававшейся разгадке несколько столетий квазифилософской головоломки: очистил комплексные числа от загадочности, показал, что они притворщики, что их кажущаяся новизна есть результат хитрой маскировки, а истинная природа почти тривиальна. Комплексное число, сказал Гамильтон, представляет собой ни больше ни меньше чем упорядоченную пару действительных чисел, снабженную конкретным списком правил сложения и перемножения пар. Мы видели также, что решение головоломки появилось слишком поздно, чтобы кого-нибудь впечатлить, и что Гаусс, когда ему пришла в голову та же идея, не потрудился даже опубликовать ее. Тем не менее размышления Гамильтона о комплексных числах оказались весьма ценными, потому что вдохновили его на создание кватернионов.

За эти и другие математические достижения в 1835 году Гамильтон был возведен в рыцарское достоинство. Кватернионы появились позже, и когда это произошло, мало кто, если не считать самого Гамильтона и нескольких почитателей, по достоинству оценил их значение. Мне кажется, при жизни Гамильтона большинство математиков и физиков рассматривало его энтузиазм в отношении кватернионов как чудачество – если не безумие в полном смысле этого слова, то нечто опасно к нему близкое. Они ошибались. Новое изобретение Гамильтона запустило настоящую революцию и завело математиков на незнакомые, неисследованные территории. Можно понять, почему большинство не сумело оценить их потенциал, но сам Гамильтон не сомневался, что наткнулся на что-то важное. Его новые территории до сих пор предлагают нам дразнящие новые открытия.

Есть вопросы, которые мало беспокоят геймеров или посетителей кинотеатров. Как работает графика? Как создаются эти иллюзии? Что делает их такими убедительными? Это понятно: не обязательно знать эти вещи, чтобы получать удовольствие от игры или просмотра фильма. Однако компании, которые специализируются на компьютерной графике и создают игры, нуждаются в большом количестве высокообразованных людей, знающих, как работают различные фокусы, разбирающихся в технических деталях и обладающих мастерством и креативностью, чтобы изобретать новые. Эта не та область деятельности, где можно почивать на лаврах.

Базовые принципы геометрии известны уже как минимум 600 лет. В эпоху итальянского Возрождения ряд видных художников начали понимать геометрию перспективного рисунка. Эта техника позволяет художнику создавать реалистичные изображения трехмерного мира на двумерном холсте. Человеческий глаз делает примерно то же самое, только роль холста играет сетчатка. Полное описание довольно сложно, но в принципе художник проецирует реальную сцену на плоский холст, проводя прямую линию от каждой точки пейзажа до точки, представляющей глаз зрителя, и отмечая место, где эта прямая достигает холста. Чудесная гравюра Альбрехта Дюрера «Художник, рисующий лютню» может служить наглядным изображением такой процедуры.

Это геометрическое описание можно перевести в простую математическую формулу, которая превращает три координаты точки в пространстве в две координаты соответствующего изображения на холсте. Чтобы применять эту формулу, нужно только знать положение холста и глаза зрителя по отношению к объекту. По практическим соображениям эту трансформацию, называемую проекцией, применяют не к каждой точке объекта, а лишь к достаточному их числу для получения хорошей аппроксимации. Эта особенность заметна и на гравюре, где видно множество точек, образующих контур лютни, а не полные ее очертания. Тонкие детали, такие как тростник на кровле или рябь на поверхности воды, а также, разумеется, цвета можно позже «наложить» на этот набор точек, пользуясь методами, которые я не буду описывать, потому что для этого потребовалась бы целая книга.

Именно это, в сущности, происходит, когда нам показывают вид деревни глазами дракона. У компьютера в памяти уже хранятся репрезентативные координаты всех значимых элементов деревни. Сетчатка драконьего глаза играет роль холста. Если мы знаем, где она находится и под каким углом располагается, то можем воспользоваться формулой и вычислить, что дракон должен видеть. Это дает один кадр фильма, который показывает зрителю деревню в конкретный момент времени. На следующем кадре деревня остается на том же месте, но дракон – и, соответственно, сетчатка его глаза – немного смещается. Вычисляем, куда именно, повторяем расчет – и получаем следующий кадр. Следуем по маршруту дракона в небесах и кадр за кадром складываем картину того, что он видит.

Гравюра «Художник, рисующий лютню» Альбрехта Дюрера иллюстрирует проецирование трехмерного пространства на двумерный холст

Это не буквальное описание процесса, разумеется, а всего лишь основная идея, лежащая в его основе. Существуют специальные приемы, позволяющие сделать расчеты более эффективными и сэкономить компьютерное время. Для простоты мы их проигнорируем.

Аналогичный расчет применяется и для сцен с приближающимся драконом, наблюдаемых с земли. Здесь нам нужно другое множество точек, определяющее положение дракона в пространстве, а экран, на который все проецируется, находится на земле, а не в глазу дракона. Для определенности возьмем вид со стороны дракона. С его точки зрения, его глаз неподвижен, зато деревня движется. По мере того как дракон подлетает ближе и проходит над деревней, все в ней зрительно увеличивается, она поворачивается и покачивается, повторяя собственные движения дракона. Если дракон взмывает в небеса, деревня уменьшается. Все это время перспектива должна оставаться убедительной, и математический ключ к этому – представление деревни в виде жесткого (и сложного) объекта. Вы можете приблизительно понять, как это происходит, если представите себя драконом, который держит перед глазами некий объект и рассматривает его, отодвигая или придвигая поближе, поворачивая так или этак.

Мы при этом представляем все в драконовой «системе отсчета», которая неподвижна относительно него. Деревня движется как жесткое целое, а это математически означает, что расстояние между любыми двумя ее точками остается неизменным. Но объект как целое может двигаться в пространстве. Существует два основных типа движения: параллельный перенос и вращение. При параллельном переносе объект скользит в некотором направлении, не наклоняясь и не разворачиваясь. При вращении объект поворачивается вокруг неподвижной прямой – оси вращения, и каждая его точка поворачивается на один и тот же угол на плоскости, перпендикулярной оси. Осью может быть любая прямая в пространстве, и угол поворота тоже может быть любым.

Любое жесткое движение является комбинацией параллельного переноса и вращения (но параллельный перенос может осуществляться на нулевое расстояние, а вращение – на нулевой угол, в этих случаях преобразования не производят никакого действия). На самом деле это неправда: существует еще один тип движения – отражение, которое работает по принципу зеркала. Но отражение невозможно получить при помощи непрерывного перемещения, так что про него можно забыть.

Ну вот, мы сделали ключевой шаг на пути превращения летающих драконов в математику. Теперь необходимо понять, как меняются координаты точки в пространстве, когда мы применяем к объекту параллельный перенос или вращение. Сделав это, мы сможем воспользоваться стандартной формулой проецирования результата на плоский экран. Оказывается, параллельный перенос никаких сложностей не представляет. Зато вращение – это большая головная боль.

В двух измерениях – на плоскости – все намного проще. Евклид формализовал геометрию плоскости примерно в 300 году до н. э. Однако он не прибегал при этом к помощи движений, а использовал конгруэнтные треугольники[6] – треугольники одинаковой формы и размера, различающиеся только положением на плоскости. К XIX веку математики научились интерпретировать такую пару треугольников как жесткое движение, то есть как такое преобразование плоскости, которое переносит первый треугольник на позицию второго. Георг Бернхард Риман определил геометрию через конкретные типы преобразований.

Следуя совсем другим путем, математики смогли также предложить эффективные способы расчета жесткого движения на плоскости – это был неожиданный побочный эффект одного нововведения в алгебре, которое мы уже упоминали в предыдущей главе: комплексных чисел. Чтобы осуществить параллельный перенос (скольжение) фигуры, например PIG (см. рис. в главе 6), мы прибавляем одно и то же комплексное число к каждой ее точке. Чтобы повернуть ее на угол A, мы умножаем каждую точку фигуры на e^iA. В качестве вишенки на торте оказалось, что комплексные числа идеальны для решения дифференциальных уравнений физики… но только в двумерном пространстве.

Все это натолкнуло Гамильтона на идею, которая вскоре захватила его. Поскольку комплексные числа так эффективны в двумерной физике, должны существовать и аналогичные им «суперкомплексные» числа, обеспечивающие те же преимущества в трех измерениях. Если бы ему удалось найти новую систему чисел, способную играть эту роль, вся реалистичная физика широко распахнулась бы перед ним. Было даже очевидно, с чего следует начать. Поскольку комплексные числа представляют собой пары действительных чисел, эти гипотетические суперкомплексные числа должны быть тройками действительных чисел. По одному действительному числу на измерение. Формула для сложения таких троек (или триплетов, как Гамильтон их часто называл) была очевидна: достаточно просто сложить соответствующие компоненты. С параллельным переносом разобрались. Оставалось найти способ перемножения триплетов. Но, что бы ни пробовал Гамильтон, с умножением у него ничего не получалось. К 1842 году его настолько захватила эта проблема, что на нее обратили внимание даже дети. Каждый день они спрашивали у отца: «Папа, ты научился перемножать триплеты?» И каждый день Гамильтон отрицательно качал головой. Складывать и вычитать – да, а перемножать – никак.

Зачастую трудно определить точную дату великого математического открытия или прорыва. Дело в том, что у подобных событий нередко длинная и запутанная предыстория. Но иногда и точная дата, и место известны. В данном случае дата – это понедельник, 16 октября 1843 года, а место – Дублин. Можно даже высказать вполне обоснованную догадку о времени, когда это произошло, поскольку Гамильтон, ставший к тому моменту президентом Королевской ирландской академии, шел с женой по тропинке вдоль канала на заседание Совета академии. Когда он остановился передохнуть на Брумском мосту, его осенило. Он увидел решение давней задачи и выцарапал его карманным ножом прямо на камнях моста.

С тех пор надпись, конечно, стерлась, но каждый год группа физиков и математиков проходит по «тропе Гамильтона», чтобы сохранить память об этом событии.

Без объяснения эта надпись безнадежно туманна. Даже с объяснением она может показаться нелепой и бессмысленной, но так часто случается с великими математическими открытиями. На их осмысление требуется время. Если бы открытием были комплексные числа, Гамильтон нацарапал бы простое правило: i² = –1. В этом уравнении – ключ ко всей системе комплексных чисел, все остальное вытекает из него, если поставить условие, что обычные правила арифметики должны соблюдаться и здесь. Добавьте к i еще j и k, и окажется, что формула Гамильтона определяет более широкую систему чисел, или, если вам так больше нравится, числоподобных объектов. Автор назвал эти объекты кватернионами, поскольку в них четыре компонента, в роли каждого из которых выступает традиционное действительное число. Вот эти компоненты: обычное действительное число; действительное число, умноженное на число i, которое ведет себя как обычное мнимое число, обозначаемое этим символом; два новых компонента – действительное число, умноженное на число j, и действительное число, умноженное на число k. Таким образом, типичный кватернион представляет собой комбинацию вида a + bi + cj + dk, где a, b, c, d – четыре обычных действительных числа. Или, если мы хотим избавиться от мистики и загадочности, это четверка (a, b, c, d) действительных чисел, подчиняющаяся короткому списку арифметических правил.

На следующий день после своего поступка, отдающего мелким хулиганством, Гамильтон написал своему другу математику Джону Грейвзу: «Меня вдруг осенило, что мы должны признать в каком-то смысле четвертое измерение пространства, чтобы проводить расчеты с тройками». В письме к отцу он отметил: «Такое впечатление, что замкнулся электрический контур и проскочила искра». В его словах было больше правды, чем ему могло показаться, потому что сегодня это открытие играет принципиально важную роль в миллиардах электрических схем, в которых задействованы квадриллионы крохотных искр. Они известны под такими названиями, как Playstation 4, Nintendo Switch и Xbox, а используются для воспроизведения таких видеоигр, как Minecraft, Grand Theft Auto и Call of Duty.

Сегодня мы понимаем, почему Гамильтону никак не удавалось перемножить триплеты. Эта операция невозможна. Он ведь считал, что обычные законы алгебры при этом должны по-прежнему действовать, в частности, что можно делить на любое ненулевое число. Однако, какую бы формулу он ни пробовал, всем необходимым правилам она подчиняться не желала. Позже алгебраисты доказали, что такие требования логически противоречивы. Если вы хотите, чтобы все законы продолжали действовать, то не можете пойти дальше комплексных чисел. Вы заперты в двух измерениях. Если поиграть с формулами Гамильтона, считая при этом, что сочетательный закон действует, можно без труда убедиться, что один из законов уже отброшен, а именно перестановочный закон умножения. Например, из его формул следует, что ij = k, тогда как ji = –k.

Гамильтону хватило воображения, чтобы отказаться от данного закона, несмотря на все затруднения, и это еще мягко сказано. Но мы сегодня знаем, что даже в этом случае невозможно построить замкнутую числовую систему троек. Красивая теорема Адольфа Гурвица, опубликованная после смерти автора в 1923 году, гласит, что действительные числа, комплексные числа и кватернионы представляют собой единственно возможные «алгебры действительного деления». То есть этот фокус можно проделывать с одним, двумя или четырьмя действительными компонентами, но не с тремя. Из перечисленных только действительные и комплексные числа подчиняются перестановочному закону. Ослабив еще и сочетательный закон, можно получить также систему с восемью компонентами, известную как октонионы, или числа Кэли. Следующим естественным числом компонентов было бы 16, но в этом случае откажет даже ослабленный вариант сочетательного закона. Вот и все. Ничего больше по указанному принципу построить нельзя. Это одна из тех странных диковинок, которые иногда выдает математика: в данном контексте следующий член в последовательности 1, 2, 4, 8, … не существует.

Так что несчастный сэр Уильям провел несколько лет в бесплодных усилиях, пытаясь достичь невозможного. Совершенный им в конечном итоге прорыв опирался на отказ от двух ключевых принципов: что умножение должно подчиняться перестановочному закону и что «правильная» числовая система для трехмерной физики должна иметь три компонента. Он заслуживает огромного уважения за то, что сумел понять: чтобы сделать шаг вперед, необходимо отказаться от обоих принципов.

Название, предложенное Гамильтоном для новой системы, – кватернионы – отражает связь с четырьмя измерениями. Он пропагандировал их использование во многих областях математики и физики, показывая, что особый тип кватерниона, его «векторная часть» bi + cj + dk, может весьма элегантно представлять трехмерное пространство. Однако кватернионы вышли из моды, когда появилась более простая структура – векторная алгебра. Они остались интересными для специалистов по чистой математике и теоретической физике, но не оправдали надежд своего создателя на широкое практическое использование. Ну, то есть до появления компьютерных игр и компьютерной графики в киноиндустрии.

Связь с кватернионами возникает потому, что объекты в компьютерной графике требуется вращать в трехмерном пространстве, а лучше всего делать это с помощью кватернионов Гамильтона. Они дают нам простой алгебраический инструмент для быстрого и точного расчета результатов вращения. Гамильтон был бы поражен, поскольку в его время кинематографа не существовало. Старая математика может находить совершенно новые сферы применения.

Предложение использовать кватернионы в компьютерной графике впервые было высказано в 1985 году в статье Кена Шумейка «Анимация вращения при помощи кватернионных кривых»{53}. Статья начиналась с утверждения: «Твердые тела вертятся и кувыркаются, двигаясь в пространстве. В компьютерной анимации то же самое делают камеры. Вращение этих объектов лучше всего описывается с использованием четырехкоординатной системы, кватернионов». Далее Шумейк заявлял, что кватернионы обладают ключевым преимуществом – позволяют гладко «заполнять промежутки», то есть интерполировать изображения между двумя заданными граничными точками.

Прежде чем разбирать подробности, имеет смысл обсудить ряд особенностей компьютерной анимации, которые обусловливают такой подход. Разговор будет сильно упрощенным, к тому же, помимо описанного, используется немало других методов. Фильм или движущееся изображение на компьютерном экране на самом деле представляет собой серию неподвижных изображений, показываемых быстро одно за другим, чтобы создать у зрителя иллюзию движения. На заре мультипликации – вспомните хотя бы мультфильмы Уолта Диснея – художники рисовали каждое из неподвижных изображений на отдельном листе. Для получения реалистичных движений (в той мере, в какой говорящая мышь может быть реалистичной) требовалось огромное мастерство. Существовали приемы, позволявшие упростить процесс. Например, иногда фон делали единым для последовательности кадров и уже на него накладывали изображения объектов, которые менялись в каждом кадре.

Это очень трудоемкий метод, к тому же он плохо подходит для съемки стремительных космических сражений или любой другой высококачественной анимации. Представьте, что вам нужно снять последовательный ряд кадров для фильма или игры, где взаимодействуют несколько звездолетов. Каждый звездолет уже прорисован и проработан (на компьютере) дизайнером. Он представлен в виде фиксированного набора точек в пространстве, связанных воедино и образующих сеть из крохотных треугольничков. Эти треугольнички, в свою очередь, могут быть представлены подходящими списками чисел – координатами точек и закодированной информацией о том, какие точки должны быть соединены друг с другом. Компьютерная программа может «отрисовать» этот набор чисел (и добавить туда другую информацию, например цвет), чтобы получилось двумерное изображение звездолета. Это изображение позволяет увидеть, как будет выглядеть звездолет, когда его поместят в начальное положение и будут рассматривать с определенного направления.

Чтобы заставить звездолет двигаться, мультипликатор меняет определяющие его числа нужным образом. Например, чтобы переместить его в новую точку, ко всем точкам прибавляют фиксированную тройку чисел (вектор смещения), тогда как связи внутри объекта остаются неизменными. Затем этот новый список чисел вновь отрисовывают, чтобы получить следующий кадр, и т. д. Прибавление вектора – операция простая и быстрая, но объекты могут также вращаться в пространстве. Они могут поворачиваться вокруг любой оси, и направление оси тоже может меняться по мере движения объекта. Повороты также меняют список чисел, но более сложным образом.

Довольно часто мультипликатор знает, откуда объект начинает движение (скажем, с поверхности Земли) и куда он должен переместиться (скажем, вдоль линии, ведущей к далекой Луне). Принципиально важно и точное положение двумерного экрана, потому что именно его видит зритель. Он должен выглядеть достаточно художественно или увлекательно, в зависимости от ситуации. Поэтому обе локации, начальная и конечная, тоже представлены тщательно рассчитанными списками чисел. Если характер движения в промежутке между ними не так важен, компьютер может получить задание интерполировать объект между начальной и конечной точками. Тогда два списка объединяются согласно определенному математическому правилу, которое представляет характер перехода от одного к другому. Усреднение каждой пары соответствующих координат, например, дает нам объект посередине между стартом и финишем. Однако такое слишком сильное упрощение неприемлемо, поскольку оно обычно искажает форму звездолета.

Фокус в том, чтобы воспользоваться для интерполяции жестким движением в пространстве. Можно, например, начать с переноса звездолета в центральную точку и поворота его на 45°. Если проделать это еще раз, звездолет окажется в конечной точке с разворотом на 90° относительно начальной ориентации. Для получения иллюзии непрерывного движения можно раз за разом переносить звездолет на 1/90 дистанции и поворачивать при этом на 1°. На практике, конечно, используются намного более мелкие шаги.

Более отвлеченно мы можем рассматривать эту процедуру с точки зрения «пространства конфигураций» всех движений. Каждая точка в этом пространстве соответствует конкретному движению, причем близкие точки дают близкие движения. Так что последовательность движений, каждое из которых близко к предыдущему, соответствует последовательности точек, каждая из которых близка к предыдущей. Связывая эти точки в упорядоченную цепочку, мы получаем ломаную траекторию в пространстве жестких движений, а очень маленький шаг делает траекторию непрерывной. Так что теперь задача заполнения промежутков от начального изображения до конечного превращается в задачу нахождения маршрута через пространство конфигураций. Если мы хотим, чтобы переход получился гладким, траектория тоже должна быть гладкой, без резких поворотов. Существуют хорошие способы сглаживания ломаной линии.

«Размерность» пространства конфигураций, то есть число координат, необходимых для определения точки в нем, равна шести. В это число входят три измерения для параллельного переноса: по одной координате для каждого направления север-юг, восток-запад, верх-низ. Еще два измерения нужны, чтобы обозначить положение оси вращения, а последнее – для угла вращения. Итак, то, что начиналось как задача о плавном движении объекта в трех измерениях, превращается в задачу о движении точки вдоль гладкой траектории в шести измерениях. Таким образом, преобразованная задача анимации может быть решена при помощи методов из многомерной геометрии, которые помогают строить подходящие траектории.

В прикладной математике традиционный подход к описанию вращения цельного объекта восходит к Эйлеру. В 1752 году он доказал, что любое движение, в котором не присутствует зеркальное отражение, представляет собой либо параллельный перенос, либо вращение вокруг оси{54}. Однако для расчетов он комбинировал три вращения вокруг трех осей в обычном координатном представлении пространства, сегодня этот метод называют эйлеровыми углами. В качестве примера Шумейк рассматривал ориентацию самолета, которая в аэронавтике определяется тремя углами:

• рысканье относительно вертикальной оси дает направление движения самолета в горизонтальной плоскости;

• тангаж – вращение вокруг горизонтальной оси, проходящей через крылья;

• крен – вращение вокруг оси, проходящей из носа в хвост.

Первая проблема такого представления состоит в том, что принципиально важен порядок, в котором применяются компоненты. Вращения не коммутативны, их нельзя переставлять местами. Вторая проблема в том, что выбор осей не является единственно возможным, и в разных сферах используются разные варианты. Третья – в том, что формулы для объединения двух последовательных вращений, выраженных через эйлеровы углы, чрезвычайно сложны. Эти особенности не вызывают чересчур больших проблем в аэродинамике, где речь идет в основном о силах, действующих на самолет, когда он находится в заданной ориентации, но для компьютерной анимации, где объекты претерпевают последовательности движений, они весьма неудобны.

Шумейк утверждал, что кватернионы обеспечивают хотя и менее непосредственный, но куда более удобный для аниматоров способ определения вращений, особенно когда дело касается заполнения промежутков. Кватернион a + bi + cj + dk расщепляется на скалярную часть a и векторную часть v = bi + cj + dk. Чтобы повернуть вектор v на кватернион q, нужно умножить v на q^-1 слева и на q справа, чтобы получить q^-1vq. Каким бы ни был q, результатом будет вновь вектор с нулевой скалярной частью. Правила перемножения кватернионов Гамильтона показывают, что любое вращение соответствует единственному кватерниону. Скалярная часть равна косинусу половины угла поворота; векторная часть направлена вдоль оси вращения и имеет длину, равную синусу половины этого угла. Так что кватернион очень аккуратно кодирует всю геометрию вращения, и единственное небольшое неудобство состоит в том, что естественные формулы работают с половиной угла, а не непосредственно с самим углом{55}.

Кватернионы позволяют уйти от искажений, которые могут накопиться, если объект проворачивается многократно, как часто и требуется. Компьютеры способны проводить точные расчеты с целыми числами, но действительные числа не могут быть представлены с абсолютной точностью, так что в результат вкрадываются крохотные ошибки. При обычных методах представления трансформаций объект, которым манипулируют, слегка меняет форму, а глаз хорошо замечает подобные вещи. Если же взять кватернион и слегка изменить в нем числа, результат по-прежнему будет кватернионом и по-прежнему будет представлять вращение, поскольку каждый кватернион представляет определенное вращение. Просто это будет чуть иное вращение, не точно совпадающее с первоначальным. К подобным ошибкам глаз значительно менее чувствителен, кроме того, если они становятся слишком большими, их несложно скомпенсировать.

Кватернионы – один из способов создания реалистичного движения в трех измерениях, но все, что я описывал до сих пор, относится исключительно к цельным, жестким объектам. К звездолетам, возможно, но к драконам нет. Драконы изгибаются. Как же получить средствами компьютерной графики реалистично движущегося дракона? Общий метод, который я буду описывать, применим не только к драконам, но почти ко всему, и мы возьмем для примера динозавра, потому что у меня есть подходящие картинки[7]. Такой подход сводит движение гибкого объекта к движению множества связанных между собой жестких объектов. Вы используете для этих жестких объектов любой метод, какой вам нравится, с дополнительными поправками, позволяющими корректно связать их воедино. В частности, если для вращения и параллельного переноса жестких объектов используются кватернионы, то эти же методы можно приспособить для работы с гибким динозавром.

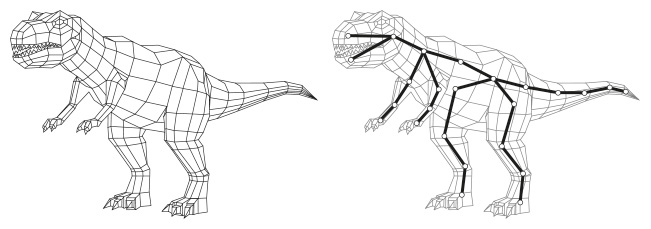
Слева: грубая полигональная сетка для Tyrannosaurus rex.

Справа: сетка, прикрепленная к рудиментарному скелету

На первом этапе создается трехмерная цифровая модель динозавра, поверхность которого представляет собой сложную сетку из плоских многоугольников – треугольников, прямоугольников, менее правильных четырехугольников. Программа, используемая для этой цели, показывает форму геометрически, и вы можете двигать объект, вращать его, приближать и т. д. Каждое движение при этом отображается на компьютерном экране. Однако непосредственно программа работает не с геометрией как таковой, а со списком координат точек, где стыкуются многоугольники. Мало того, математика, которую при этом использует программа, помогая рисовать динозавра, примерно та же, что задействуется для анимации результата. Основное различие состоит в том, что на этом этапе динозавр как бы закреплен, а вращается и переносится точка наблюдения. При анимации закрепленной может быть точка наблюдения, а динозавр движется, или, как с летящим драконом, точка наблюдения может двигаться тоже.

Так что теперь у нас имеется грубый и жесткий динозавр. Как заставить его двигаться? Чего мы точно не делаем, так это того, что приходилось делать художникам во времена Микки-Мауса: мы не перерисовываем изображение с динозавром в чуть разном положении сотни раз. Мы хотим, чтобы компьютер делал за нас всю рутинную работу. Поэтому мы сводим нашего динозавра к рудиментарному скелету – небольшому числу жестких стержней («костей»), концы которых соединены. Мы пропускаем эти стержни через туловище, конечности, хвост и голову динозавра. Это не анатомически корректный скелет, а просто рамка, которая позволяет изгибать основные части животного. Скелет также представлен в виде списка координат для двух концов каждой кости.

Очень эффективный способ получения реалистичных движений, особенно людей и других гуманоидных существ, – захват движения. Актер проделывает необходимые движения перед камерой или несколькими камерами, если нужно получить трехмерные данные. При этом на ключевых точках его тела, таких как ступни, колени, бедра и локти, закрепляются белые кружки (точки), а затем компьютер, анализируя полученное видео, получает данные о движении этих точек. Эти данные используются для анимации скелета. Именно так был анимирован Голлум в трилогии «Властелин колец». Естественно, если вам нужны странные нечеловеческие (но при этом реалистичные) движения, то и актеру приходится двигаться соответствующим образом.

Каким бы способом ни анимировался скелет, как только результат нас устраивает, мы «набрасываем» на него подготовленную сетку. То есть мы объединяем два списка координат, определяя дополнительные связи между положением костей и положением окружающих их кусочков сетки. Затем на большую часть процесса мы забываем о сетке и занимаемся исключительно анимацией скелета. Именно на этом этапе очень кстати оказывается наша работа, связанная с жестким движением, потому что каждая кость является жесткой, и мы хотим, чтобы они двигались в трех измерениях. Кроме того, мы должны наложить на движение ограничения, благодаря которым скелет будет оставаться целым. Если мы двигаем одну кость, концы костей, прикрепленных к ней, тоже должны сдвинуться, так что мы переносим координаты этих концов в правильные позиции. Затем можно жестко двигать и эти кости тоже, что, конечно, влияет на кости, прикрепленные уже к ним… так, кость за костью, мы заставляем весь скелет слегка изогнуться. Можно сдвинуть ступни, чтобы заставить динозавра идти, изогнуть хвост вверх, вниз или в сторону, открыть ужасные челюсти – но все это мы проделываем на скелете. Это проще, быстрее и дешевле, потому что у скелета намного меньше частей.

Когда характер движений скелета нас устраивает, мы набрасываем на скелет сетку, начиная с первого кадра движения. А программа анимации заставляет следовать за движениями скелета на последовательных кадрах, причем нам уже не нужно ничего делать, за исключением, возможно, одного-двух кликов мышкой. Это позволяет убедиться, что анимация по-прежнему выглядит реалистично, когда весь динозавр следует за тем, что происходит с его скелетом.

Далее можно заняться творчеством и поиграть разными параметрами. Мы можем сдвигать положение «камеры», менять точку зрения, используемую программой, приближать объекты, получая крупный план, или, наоборот, рассматривать бегущего динозавра издалека – все что угодно. Мы можем создавать других существ, например стадо травоядных, убегающих от чудовищного тираннозавра. Делается это аналогично – сначала скелеты, на которые затем набрасывается сетка. Можно анимировать каждое существо отдельно, а затем собрать их вместе в единую сцену охоты хищника.

Поскольку скелеты – это всего лишь схематичные фигурки, на этом этапе мы, пожалуй, еще ничего не сделали, чтобы предотвратить появление двух существ в одном и том же объеме пространства. Дополнительные настройки программы позволяют ей предупреждать нас о столкновениях такого рода. Когда мы набрасываем на скелеты сетки, те многоугольники, которые оказываются впереди, перекрывают те, что сзади, и, поскольку динозавры непрозрачны, приходится убирать те области, которые должны быть скрыты. Все это делается при помощи простых вычислений координатной геометрии, но таких вычислений оказывается довольно много. До тех пор пока компьютеры не стали по-настоящему быстрыми, это было невыполнимо. Теперь это рутина.

Дел остается еще немало, поскольку динозавр, похожий на скопище многоугольников, не слишком впечатляет. Нужно задрапировать многоугольники реалистичным кожным узором, затем разобраться в цветовой информации, может быть, создать какие-то реалистичные текстуры – мех выглядит совсем иначе, нежели чешуя. Каждый шаг требует отдельного программного обеспечения и применения соответствующих математических методов. Этот этап называется отрисовкой, и именно на нем собирается окончательная картинка, которая появляется на экране, когда мы смотрим кино. Но в сердце всего лежат миллиарды вычислительных операций, обеспечивающих жесткое движение точек и ребер.

Эти математические методы обладают и еще одним преимуществом. На любом этапе, когда нас что-то не устраивает, мы можем изменить соответствующую деталь. Если мы хотим, чтобы динозавр был зеленым, а не коричневым, то не нужно перерисовывать все заново. Мы воспользуемся тем же скелетом и той же сеткой, возьмем те же движения и ту же текстуру кожи, но поменяем ее цвет.

Занимаясь созданием фильма или игры, команды специалистов используют целый ряд стандартных пакетов программ, разработанных для обеспечения этих процессов. Чтобы дать вам хотя бы примерное представление о сложности происходящего, я назову некоторые из компаний и программных пакетов, использованные при создании фильма «Аватар».

Основной объем анимации обеспечивала компания Weta Digital в Новой Зеландии, известная своей работой над «Властелином колец» и «Хоббитом». Почти две сотни видеопоследовательностей – в основном это были летательные аппараты в финальном сражении – создала компания Industrial Light & Magic, основанная в 1975 году Джорджем Лукасом для создания спецэффектов для первого фильма саги «Звездные войны». Остальные компании из Великобритании, Канады и США добавляли к изображению важные детали, такие как экраны в аппаратной и информационные табло на забралах шлемов, имитирующие технологии будущего. Большая часть подобных кадров была сделана в редакторе Autodesk Maya. Дизайн моделей летательных аппаратов, в особенности Scorpion, был сделан в программе MODO компании Luxology. Сцены в поселке Хеллс-Гейт и интерьеры создавались в редакторе трехмерной графики Houdini. Инопланетные существа были нарисованы с помощью ZBrush. Первоначальный концепт и текстуры создавались при помощи программы Adobe Photoshop. Всего в работе над фильмом участвовало около десятка компаний и использовалось 22 пакета программ плюс бесчисленные специально написанные плагины.

В настоящее время комплекс инструментов, применяемых для компьютерной анимации, пополняют кое-какой весьма хитроумной математикой. Цель, как всегда, – сделать задачу аниматора как можно более простой, получить реалистичный результат и снизить затраты денег и времени. Мы хотим всё, причем сразу и дешево.

Предположим, например, что у киностудии имеется библиотека анимаций динозавра, содержащих последовательности его движений. В одной он несется вперед, совершая один «цикл бега», то есть один сегмент периодически повторяющегося движения. В другой – подпрыгивает и приземляется. Вам нужно создать последовательность, в которой он гонится за небольшим травоядным животным и прыгает на него. Эффективным началом работы над этой последовательностью будет сшивание десятка-другого циклов бега и добавление в конце прыжка. Конечно, затем придется чуть-чуть все поменять, чтобы зрителю не было видно, что повторяется одна и та же анимация, но для начала это совсем неплохо.

Разумно сшивать и выстраивать последовательности на уровне скелета. Все остальное – набросить сетки, добавить цвет и текстуру – можно сделать позже. Поэтому вы делаете очевидное – соединяете подряд 12 копий цикла бега и прыжок и смотрите, как выглядит результат.

Он выглядит ужасно.

Отдельные кусочки ничего, но друг с другом они гладко не стыкуются. Результат получается дерганым и неубедительным.

До недавнего времени единственным выходом была модификация стыков вручную с интерполяцией новых небольших кусочков движений. Но это было не очень просто. Однако кое-какие недавние новинки в области математических методов обещают облегчить эту задачу. Идея заключается в использовании методов сглаживания для заполнения прорех и выравнивания резких переходов. Главное – найти способы делать это с единичной костью скелета или, в более общем случае, с единичной кривой. Решив такую задачу, можно вновь сшить скелет воедино из отдельных костей.

Область математики, которую сейчас пытаются применить, называется теорией форм. Поэтому начнем с очевидного вопроса: что такое форма?

В обычной геометрии встречается множество стандартных форм: треугольник, квадрат, параллелограмм, окружность. При интерпретации в координатной геометрии эти формы превращаются в уравнения. На плоскости, например, точки (x, y) на единичной окружности в точности удовлетворяют уравнению x² + y² = 1. Еще один очень удобный способ представления окружности состоит в использовании так называемого параметра. Это вспомогательная переменная, скажем t, которую мы можем рассматривать как время, вместе с формулами, определяющими, как x и y зависят от t. Если t принимает ряд численных значений, то каждое его значение дает нам две координаты x(t) и y(t). Возьмите правильные формулы, и эти точки определят окружность.

Стандартные параметрические формулы для окружности имеют тригонометрический характер:

Можно также изменить вид параметра в формуле и все равно получить окружность. Например, если заменить t на t³, то формулы

тоже определяют окружность, причем ту же самую. Такой эффект наблюдается потому, что параметр времени несет больше информации – не только о том, как меняются x и y. Согласно первой формуле, точка при изменении t движется с постоянной скоростью. Согласно второй формуле, нет.

Теория форм – это способ обойти проблему неопределенности. Форма – это кривая, которая рассматривается как объект, не зависящий от конкретной параметрической формулы. Так что две параметрические кривые определяют одну и ту же форму, если можно изменением параметра превратить одну формулу в другую, как при замене t на t³. За последнее столетие математики придумали общепринятый способ делать подобные вещи. Никто другой, скорее всего, об этом не подумал бы, потому что для этой идеи требуется абстрактное мышление.

Первый шаг заключается в том, чтобы рассматривать не просто одну параметрическую кривую, а «пространство» всех возможных параметрических кривых. Тогда мы говорим, что две «точки» в этом пространстве (то есть две параметрические кривые) эквивалентны, если можно перейти от одной из них к другой посредством изменения параметра. Тогда «форма» определяется как целый класс эквивалентности кривых – множество всех кривых, эквивалентных данной.

Это более обобщенный вариант приема, используемого в модулярной арифметике. Для целых чисел по модулю 5, например, «пространство» – это все целые числа, а два целых числа эквивалентны, если их разность кратна пяти. Существует пять классов эквивалентности:

Почему здесь следует остановиться? Потому что число, кратное 5, при добавлении 5 становится всего лишь следующим кратным 5.

В данном случае множество классов эквивалентности, обозначаемое Z₅, обладает весьма полезной структурой. И правда, глава 5 показала, что значительная часть фундаментальной теории чисел опирается именно на эту структуру. Мы говорим, что Z₅ – это «фактор-пространство» целых чисел по модулю 5. Именно его вы получите, если сделаете вид, что числа, различающиеся на 5, идентичны.

Нечто аналогичное приводит нас к созданию пространства форм. Здесь вместо целых чисел мы имеем пространство всех параметрических кривых. Вместо того чтобы менять числа на кратное 5, мы меняем формулу параметра. Так что в конечном итоге мы получаем «фактор-пространство», то есть пространство всех параметрических кривых по модулю изменений параметра. Звучит, возможно, бессмысленно, но это давно уже ставший стандартным прием, ценность которого подтверждена временем. Одна из причин его ценности в том, что фактор-пространство – это естественное описание интересующих нас объектов. Другая – в том, что обычно фактор-пространство наследует от исходного пространства его интересную структуру.

Для пространства форм основной интересной особенностью структуры является мера расстояния между двумя формами. Если взять окружность и слегка ее деформировать, мы получим замкнутую кривую, близкую к окружности, но не совпадающую с ней. Если деформировать окружность сильно, получим замкнутую кривую, которая, на интуитивном уровне, отличается от окружности сильнее: она «дальше» от окружности. Это интуитивное представление можно сделать более точным и доказать, что в пространстве форм есть разумная и естественная концепция расстояния: метрика.

Если пространство обладает метрикой, в нем можно делать множество разных полезных вещей. Можно, в частности, отличать непрерывные изменения от тех, которые непрерывными не являются, а можно пойти дальше: отличать плавные изменения от неплавных. Здесь, наконец, мы возвращаемся к проблеме сшивания анимационных последовательностей. Метрика пространства форм позволяет как минимум находить разрывы непрерывности или недостаток плавности на компьютере, посредством вычислений, а не на глаз. Но это еще не все.

В математике много методов сглаживания, способных превратить функцию с разрывами в непрерывную функцию, а негладкую функцию – в гладкую. Как выяснилось, эти методы можно применять и к пространству форм. Так что сшитую последовательность с внезапным разрывом непрерывности можно автоматически – посредством надлежащих компьютерных расчетов – модифицировать и, таким образом, избавиться от разрыва. Это непросто, но возможно. Даже в простом расчете расстояния между двумя кривыми используются методы оптимизации, немного похожие на те, что мы встречали в рассказе о задаче коммивояжера. Для сглаживания последовательности необходимо решить дифференциальное уравнение, напоминающее уравнение Фурье для теплопередачи, которое мы встретим в главах 9 и 10. Теперь вся анимированная последовательность кривых «перетекает» в другую анимированную последовательность, сглаживая при этом все нарушения непрерывности и плавности – и это опять же похоже на то, как тепловой поток сглаживает прямоугольный импульс{56}.

Кроме того, аналогичные абстрактные формулировки делают возможным перевод анимационных последовательностей в похожие, но другие. Последовательность, показывающую, как динозавр идет, можно при помощи небольших поправок изменить так, что животное побежит. Для этого недостаточно просто ускорить действие, потому что бег динозавра зрительно отличается от его ходьбы. Эта методология пока еще находится в начале своего развития, но она позволяет надеяться, что в будущих кинематографических спецэффектах важную роль будет играть математическая мысль очень высокого уровня.

Это всего лишь некоторые из методов, привнесенных в мультипликацию математикой. Другие методы создают упрощенные варианты физических процессов для имитации волн на поверхности океана, сугробов, облаков и гор. Их цель в том, чтобы получить реалистичные результаты, пользуясь как можно более простыми расчетами. В настоящее время существуют масштабные математические теории о представлении человеческих лиц. В фильме «Изгой-один», который является частью сериала «Звездные войны: Истории», актеров Питера Кушинга (умершего в 1994 году) и Кэрри Фишер (умершую в 2016 году) воссоздали в цифровом формате, наложив их лица поверх лиц их телесных двойников. Получилось не слишком убедительно, и фанаты шумно протестовали. В «Последнем джедае» воспользовались более подходящим методом: нарезали из материала, не вошедшего в предыдущие фильмы, кадров с Фишер и сшили их воедино, адаптировав сценарий под имеющийся видеоряд. Тем не менее потребовалось немало компьютерной графики, чтобы заменить на персонаже одежду для единства сюжета. Мало того, почти все, за исключением лица, было отрисовано в цифровом формате – голова, прическа, тело, одежда{57}.

Эти методы уже используются для создания «глубоких фейков» в политической борьбе. Достаточно снять, как какой-то человек делает расистские или сексистские замечания или ведет себя как пьяный, а затем наложить поверх лица этого человека лицо вашего оппонента и выложить ролик в социальные сети. Даже если выяснится, что это фейк, вы все равно останетесь в выигрыше, потому что слухи распространяются куда быстрее фактов. Математика и технологии, на ней основанные, могут нести как зло, так и благо. Все зависит от того, в чьих они руках.