Это база: Зачем нужна математика в повседневной жизни

4 Почки Кёнигсберга

На протяжении большей части человеческой истории органы, с которыми люди рождались, оставались с ними до самой смерти и зачастую становились ее причиной. Если отказывало сердце, или печень, или легкие, или кишечник, или желудок, или почки, то человек просто умирал. Некоторые части тела, прежде всего конечности, можно было хирургически удалить, и если человек выдерживал это мероприятие, то он мог существовать и дальше. Появление анестетиков и создание стерильных условий в операционных сделали хирургические операции менее болезненными, по крайней мере пока пациент был без сознания, и сильно увеличили шансы больного на выживание. Антибиотики позволили справляться с инфекциями, которые прежде были фатальными.

Мы воспринимаем эти чудеса современной медицины как нечто само собой разумеющееся, но именно они, по существу, впервые дали возможность врачам и хирургам излечивать болезни. Мы умудрились растранжирить большую часть преимуществ антибиотиков в результате массового скармливания их скоту не ради лечения болезней, а чтобы заставить животных увеличиваться в размерах и расти быстрее. И еще в результате того, что миллионы людей прекращали принимать таблетки, как только им становилось лучше, вместо того чтобы пройти полный курс лечения, предписанный врачом. Обе практики привели к развитию устойчивости к антибиотикам у бактерий. Теперь ученые лихорадочно пытаются получить антибиотики следующего поколения. Если им удастся это сделать, я надеюсь, нам хватит здравого смысла не погубить и эти лекарства.

Сегодня становится реальностью и другая мечта хирургов прошлого: пересадка органов. Пока нам, кажется, удается не испортить здесь ничего. Если обстоятельства складываются благоприятно, вы можете получить новое сердце, или новое легкое, или новую почку. Даже новое лицо. Когда-нибудь добрая свинка даже сможет вырастить для вас орган на замену, хотя и не добровольно.

В 1907 году американский медик-исследователь Саймон Флекснер, рассуждая о будущем медицины, предвидел появление возможности хирургической замены больных органов на здоровые от другого человека. Он называл в их числе артерии, сердце, желудок и почки. Первую пересадку почки провел в 1933 году советский хирург Юрий Вороной, который изъял почку у донора, умершего за шесть часов до этого, и пересадил ее пациентке в область бедра. Пациентка умерла через два дня, когда новая почка была отторгнута, потому что у донора была неподходящая группа крови. Самым серьезным препятствием для успешной пересадки органов является иммунная система организма, которая распознаёт новый орган как чужеродный и отторгает его. Первую успешную пересадку почки осуществил Ричард Лоулер в 1950 году. Донорская почка функционировала 10 месяцев, прежде чем была отторгнута, но к тому времени собственные почки пациентки пришли в норму, и женщина прожила еще пять лет.

Человек имеет две почки и вполне может жить с одной. Так что органы для пересадки могут быть получены от живого донора, что сильно упрощает процесс. Почка – самый простой орган для пересадки. Не так уж сложно убедиться, что ткани донора соответствуют по типу тканям реципиента и не будут отторгнуты, а на случай, если что-то пойдет не так, имеются диализные аппараты, которые выполняют функции почки. До появления в 1964 году иммунодепрессантов, предотвращающих отторжение донорской почки, пересадка почек от умерших доноров не проводилась (по крайней мере, в США и Великобритании). Почки для пересадки жертвовали живые доноры, и таких случаев было немало.

В большинстве случаев донор был близким родственником реципиента. Это повышало вероятность совместимости тканей, но главной причиной было то, что мало кто готов был пожертвовать свою почку чужому человеку. В конце концов, если у вас есть вторая, вы можете и дальше жить нормальной жизнью, если одна почка вдруг откажет. Если отдать одну почку постороннему человеку, резерва не останется. Когда же реципиент – ваша мать, брат или дочь, то спасение их жизни перевешивает риск. Проблема постороннего человека воспринимается не так близко к сердцу, и готовых пойти на риск не так много.

Некоторые страны предлагали стимул: деньги. Можно было заплатить постороннему человеку, чтобы он пожертвовал почку одному из ваших родственников. Опасности, связанные с разрешением такого рода операций, достаточно очевидны: нужда, например, может заставить бедных продавать почки богатым. В Великобритании закон прямо запрещал отдавать почку кому-либо, кроме близкого родственника. Законы, принятые в 2004 и 2006 годах, устранили это препятствие, но добавили дополнительные меры против злоупотреблений. Одним из условий стал запрет на передачу каких бы то ни было денег.

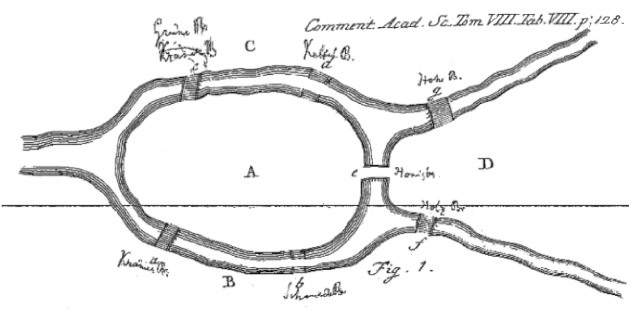
Схема расположения семи мостов Кёнигсберга, сделанная Эйлером

Эти изменения в законодательстве открыли путь для новых стратегий поиска доноров и позволили резко повысить число операций. Они также поставили перед специалистами немало математических задач, связанных с эффективным использованием этих стратегий. При этом выяснилось, что инструменты для решения подобных задач уже существуют. Все началось почти 300 лет назад с одной маленькой головоломки.

Это хорошо известная история, но я все равно перескажу ее, по двум причинам. Она готовит сцену для математической задачи и, кроме того, часто воспринимается неверно. Я, например, до какого-то момента понимал ее совершенно неправильно.

Калининград, город в сегодняшней России, когда-то назывался Кёнигсбергом и в XVIII веке находился в Пруссии. Через город протекала река Прегель, образуя два острова, Кнайпхоф и Ломзе. В городе было семь мостов: каждый из берегов реки связывали с Кнайпхофом по два моста; с Ломзе берега связывало по одному мосту; и наконец, один мост соединял острова друг с другом. Сегодня топография города выглядит иначе. Во время Второй мировой войны город сильно бомбили, и мосты b и d на схеме были разрушены. Мосты a и c были снесены, чтобы освободить место для прокладки новой дороги, а взамен них были выстроены новые мосты. Вместе с оставшимися тремя мостами, один из которых был перестроен в 1935 году, сейчас в городе на прежних местах находятся пять мостов.

Легенда гласит, что граждан Кёнигсберга давно интересовал вопрос, можно ли совершить пешую прогулку по городу, пройдя по каждому из мостов ровно один раз. Это была простенькая головоломка из разряда тех, что можно увидеть на странице газеты или ее электронного эквивалента. Эксперименты с различными маршрутами не помогают ее решить – попробуйте сами. Однако аналогичные задачи имеют решение, причем иногда найти их непросто. Более того, число маршрутов, которые вы можете выбрать, бесконечно, хотя бы потому, что существует бесконечно много способов переходить с одной стороны улицы на другую или двигаться вперед и назад. Именно поэтому невозможно найти решение или доказать, что такового не существует, путем рассмотрения всех возможных маршрутов.

Можно, конечно, решить эту головоломку, придумав какую-нибудь хитрость. Например, зайти на мост, прогуляться по нему до противоположного берега и, не сходя на берег, развернуться и пойти назад, сказав при этом, что «прошел» по мосту. Но условие «прохождения» по мосту должно быть таким, чтобы исключать подобные фокусы. Аналогично «пешая прогулка» подразумевает, что нельзя проделать часть пути вплавь, на лодке, на воздушном шаре или принадлежащей доктору Кто машине TARDIS. Или пройти вверх по реке до какого-нибудь моста, который не вошел в схему Эйлера. Хотя «стряпать» головоломки таким образом может быть интересно и даже требовать немалой изобретательности, понятно, что это все же жульничество. Я не собираюсь тщательно формулировать все до единого условия, необходимые, чтобы исключить стряпню подобного рода. Меня гораздо больше интересует, как, переведя эту головоломку на язык математики, доказать невозможность отыскания ее решения, не прибегая к стряпне. Стряпня здесь заключается в формулировании этой задачи, а не в ее решении или доказательстве невозможности найти решение, если она уже сформулирована.

И тут на сцене появляется Эйлер, ведущий математик своего времени. Он работал практически во всех областях математики, существовавших на тот момент, и в некоторых областях, которых не существовало, пока он не положил им начало. Кроме того, Эйлер сумел применить математику к огромному числу разнообразных задач реального мира. Его работы варьируют от энциклопедических томов по основным областям чистой математики и математической физики до диковинок и странностей, которые просто показались ему интересными. В начале XVIII века он обратился к загадке о кёнигсбергских мостах, сформулировал ее как точный математический вопрос и предложил доказательство того, что прогулку с обозначенными условиями совершить невозможно. Причем невозможно даже в том случае, если маршрут будет не круговым и закончится не там, где начался.

Эйлер переехал в Россию, в Санкт-Петербург, в 1727 году, когда в России правила императрица Екатерина I, чтобы стать придворным математиком. Муж Екатерины император Петр I основал Санкт-Петербургскую академию (Academia Scientiarum Imperialis Petropolitinae) в 1724–1725 годах, но умер прежде, чем она успела полностью сформироваться и заработать. Эйлер представил свою работу в Академии в 1735 году, и через год она была опубликована. Будучи математиком, причем, по мнению многих, самым плодовитым в истории, Эйлер извлек из головоломки так много, как только смог: он нашел необходимые и достаточные условия для существования решения, не только для кёнигсбергских мостов, но и для любой задачи подобного рода. Вы можете взять 50 000 мостов, связывающих друг с другом 40 000 островов гигантского комплекса, и теорема Эйлера без проблем скажет вам, существует ли для них решение. Если как следует вникнуть в доказательство, оно даже скажет, как это решение найти, – правда, после некоторой возни. Свое доказательство Эйлер изложил довольно схематично, и прошло почти 150 лет, прежде чем кто-то разобрался во всех его деталях, хотя само по себе доказательство не было слишком сложным.

В настоящее время многие книги по теории графов говорят о том, что Эйлер доказал отсутствие у головоломки решения, сведя ее к более простому вопросу о графах. Граф в этом смысле – это множество точек (называемых вершинами), соединенных линиями (их называют ребрами), и все это вместе образует своего рода сеть{34}. Переформулирование с использованием графов превращает головоломку кёнигсбергских мостов в задачу нахождения пути на конкретном графе, в котором каждое ребро используется ровно один раз. Именно так мы решаем эту задачу сегодня, но Эйлер делал не совсем так. В истории это случается часто. Историки математики с удовольствием рассказывают о том, как все происходило на самом деле, в отличие от общепринятого варианта. В реальности Эйлер решил задачу символически{35}.

Он обозначил каждый участок суши (остров или берег реки) и каждый мост буквой. Суше достались заглавные буквы A, B, C, D, а мостам – строчные a, b, c, d, e, f, g. Каждый мост соединяет друг с другом два участка суши, например, мост f соединяет A и D. Прогулка начинается в некоторой области и может быть описана последовательным перечислением преодоленных участков и мостов до последнего участка суши. В большей части статьи Эйлер описывает маршруты словесно и в основном работает с последовательностью участков суши. Не имеет значения, по какому мосту вы перейдете с A на B, если число сочетаний AB будет равно числу таких мостов. Или можно, наоборот, использовать последовательность мостов – достаточно обозначить точку начала и подсчитать, сколько раз вы посетите заданный участок. Не исключено, что так было бы проще. Ближе к концу статьи Эйлер использует те и другие символы и приводит пример последовательности

соответствующий более сложной схеме{36}.

В такой формулировке конкретный путь, по которому идет пешеход на каждом участке или по каждому мосту, не имеет значения. Единственное, за чем нужно следить, – это последовательность, в которой посещаются участки и проходятся мосты. Проход по мосту подразумевает, что «две заглавные буквы с обеих его сторон различны». Это исключает возможность зайти на мост и возвратиться на ту же сторону. Решение – последовательность чередующихся заглавных и строчных букв A–D и a–g, в которой каждая строчная буква появляется ровно один раз, а заглавные буквы до и после любой заданной строчной соответствуют тем двум участкам берега, которые связаны данным мостом.

Мы можем составить список связей для каждой строчной буквы:

Допустим, мы начинаем с участка B. Три моста связывают B с другими участками: a, b и f. Предположим, мы выбираем f, тогда наша последовательность начинается с Bf. На другом конце моста f находится участок D, так что мы получаем Bf D. У нас имеются два неиспользованных моста, связывающие D с другими участками: e и g. (Мы не можем использовать f второй раз.) Попробуем g, и наш маршрут будет выглядеть как BfDg. На другом конце g находится C, что дает нам BfDgC. Теперь единственная возможность для продолжения у нас – мосты c и d (вновь по g мы идти не можем). Возможно, мы попробуем мост c, что приведет нас к BfDgCc, а затем к BfDgCcA. От участка A идут четыре возможных моста: a, b, d и e (мост c мы уже использовали).

Можем ли мы теперь выбрать мост d? Нет, потому что это даст нам BfDgCcAd и затем BfDgCcAdC. Но все три моста, связанные с C, а именно c, d и g, уже использованы. Но мы не решили головоломку, потому что мост b остался незадействованным: мы по нему не прошли. Стираем мост d. По аналогичным причинам мы не можем воспользоваться и мостом e: это приведет нас на D, где мы и застрянем; более того, по b опять пройти не удалось. Как насчет моста a? Это дает нам BfDgCcAaB, и единственным неиспользованным выходом остается мост b, что дает нам BfDgCcAaBbA. Возможные выходы здесь – d или e. Первый ведет к BfDgCcAaBbAdC, и дальше выхода не остается, но мы не прошли по мосту e. Второй ведет к BfDgCcAaBbAeD, и тоже выхода нет, но мы не прошли по мосту d.

Ну хорошо, такая последовательность выбора не работает, но ведь мы могли выбрать другие мосты раньше. Можно проработать систематически все возможные последовательности… и окажется, что все они не годятся и могут быть исключены. В какой-то момент вы оказываетесь в тупике, не имея разрешенного выхода с текущего участка, но при этом по крайней мере один мост остается непройденным. Список возможных последовательностей конечен и не так уж велик, чтобы протестировать их все. Попробуйте, если хотите.

Если вы это сделаете, то увидите, что у данной головоломки нет решения. Это могло бы удовлетворить граждан Кёнигсберга, но не Эйлера. Во-первых, неясно, почему вы каждый раз упираетесь в тупик. Во-вторых, этот ответ ничего не говорит о том, в каких случаях можно или нельзя решить другие подобные головоломки. Поэтому Эйлер задал единственный и самый важный вопрос, который математики всегда задают после решения задачи: «Да, но почему это сработало?» За ним обычно следует другой, не менее важный вопрос: «Можно ли улучшить решение?»

Эйлер после размышлений сделал три простых наблюдения:

• Если решение существует, то каждый участок должен быть соединен с остальными какой-то последовательностью мостов. Например, если бы в городе было еще два острова E и F, соединенных друг с другом одним или несколькими новыми мостами h, i, j, …, при отсутствии новых мостов между этими островами и остальными участками суши, то пройти по ним можно было бы, лишь курсируя по ним с E на F и обратно. Ни на один из старых мостов попасть оттуда было бы невозможно.

• Считая, что предыдущее условие («связность») соблюдено, можно сказать, что, исключая участки в начале и в конце прогулки, всякий раз, когда вы входите на какой-то участок суши, с него нужно выйти по другому мосту.

• Всякий раз, когда вы это делаете, вы используете два моста, примыкающие к данному участку, которые перестают быть доступными.

Таким образом, двигаясь по маршруту, вы используете мосты парами. Это ключевой вывод. Если на участке суши четное число мостов, вы можете использовать их все и не оказаться в тупике. Если там нечетное число мостов, то вы можете использовать их все, кроме одного, и не застрять. Но вы должны пройти по этому мосту в какой-то момент. Но стоит это сделать – и вы в тупике.

Застревание фатально, если вы находитесь в середине пути. Однако это не проблема в конце. Если же пройти маршрут в обратном направлении, то станет понятно, что это не проблема и в начале прогулки. Из этих рассуждений следует, что если маршрут существует, то максимум два участка суши в нем могут быть связаны нечетным числом мостов. В задаче о мостах Кёнигсберга:

Здесь число участков суши с нечетным количеством мостов равно четырем, а это больше двух. Так что нужного нам маршрута не существует.

Разомкнутый маршрут с использованием пяти оставшихся мостов

Эйлер также заявил без доказательства, что это же условие четности/нечетности является достаточным для существования маршрута. Это немного сложнее, и я не буду здесь останавливаться. Доказал это утверждение Карл Хирхольцер незадолго до своей смерти в 1871 году, а опубликовано доказательство было посмертно в 1873 году. Эйлер также заметил, что если искать замкнутый маршрут, который заканчивался бы там же, где начался, то необходимое и достаточное условие его существования состоит в том, что на каждом участке суши должно быть четное число мостов{37}.

Если использовать только те пять мостов, которые (в том или ином виде) существуют и сегодня, то B и C оказываются связанными двумя мостами. В таком виде эта задача должна иметь решение, но только для разомкнутого маршрута. Конечные точки должны располагаться на A и D, потому что именно эти участки суши по-прежнему связаны нечетным числом мостов. На рисунке показано такое решение. Существуют и другие: сможете ли вы найти все?

Слева: граф, показывающий связи для мостов Кёнигсберга.

Справа: пример попытки составить маршрут – мост d пропущен

Эйлер сформулировал все вышеизложенное в виде символьных последовательностей вроде BfDgCcAaBbAeD. Некоторое время спустя кто-то догадался, что всему этому можно дать графическую интерпретацию. Кто был первым – неясно, поскольку в середине XIX века эта идея уже витала в воздухе, однако известно, что термин «граф» предложил в 1878 году Джеймс Джозеф Сильвестр. Нарисуйте картинку с четырьмя точками A–D и семью линиями a–f. Сделайте так, чтобы каждая линия соединяла две области на концах соответствующего моста. Карта островов и мостов при этом упрощается, как на рисунке слева. Только что упомянутая символьная последовательность соответствует маршруту на картинке справа с началом в точке B и концом в точке D, где движение прекращается.

Это визуальное упрощение и есть граф кёнигсбергских мостов. В данном представлении неважно, где вы поставите четыре точки (хотя их следует ставить на некотором расстоянии друг от друга, чтобы избежать путаницы), да и конкретная форма линий тоже не имеет значения. Важно лишь, какие именно точки соединяет данная линия. В этой визуальной среде доказательство Эйлера становится очень естественным. Любой маршрут, который входит на участок суши по одному мосту, должен уйти с него по другому, если это не конец разомкнутого маршрута. Аналогично любой маршрут, покидающий участок по одному мосту, должен был ранее входить на него по другому, если это не начало разомкнутого маршрута. Так что мосты должны существовать парами, за исключением двух концов. Следовательно, все участки суши, расположенные не на концах маршрута, связаны с четным числом мостов. Если на концах число мостов нечетное, возможен только незамкнутый маршрут. В противном случае начало и конец могут находиться в одной области и соединяться без всяких мостов, образуя замкнутый маршрут. Теперь к каждой области подходит четное число мостов.

Решением этого единственного класса задач Эйлер дал старт двум важным областям математики. Одна из них – теория графов, которая изучает точки, соединенные линиями. Звучит очень просто, даже как-то по-детски. Так и есть. Но в то же время это глубоко, полезно и сложно, как мы увидим. Вторая – топология, которую иногда называют «геометрией резинового листа», где фигуры могут деформироваться непрерывно и при этом не считаться существенно различными. Здесь формы линий и расположение точек могут меняться как угодно при условии, что не меняется способ их соединения (требование непрерывности), и получается, по существу, тот же граф. Тот же в том смысле, что сообщает ту же информацию о том, что с чем соединяется.

Мне кажется замечательным, что простая головоломка может привести к таким значительным нововведениям. Воистину непостижимая эффективность. Кроме того, в этой истории содержится важный урок, который внешний мир зачастую не воспринимает. Не стоит недооценивать математику, которая выглядит просто и больше похожа на детскую игрушку, чем на что-нибудь серьезное. Дело не в том, насколько проста игрушка, а в том, как вы ее используете. Мало того, одна из главных задач хорошей математики состоит в том, чтобы сделать все как можно более простым. (Вы можете усмехнуться, и это будет справедливо, если вспомнить, насколько сложно выглядит значительная часть математики. Я просто должен здесь добавить оговорку, приписываемую Эйнштейну: как можно более простым, но не слишком простым.) Превращение островов в точки, а мостов в линии не меняет сути головоломки, а помогает отбросить лишнюю информацию: какая стоит погода? Грязно ли на улице? Мост металлический или деревянный? Эти вещи важны, если вы собираетесь на субботнюю прогулку или строите мост. Но если вы хотите ответить на вопрос, который ставил в тупик добрых граждан Кёнигсберга, все это лишь помехи.

Ну а какое отношение мосты Кёнигсберга имеют к трансплантации почек? Непосредственно почти никакого. Косвенно статья Эйлера положила начало развитию теории графов, которая открывает перед нами эффективный способ подбора доноров для реципиентов даже при условии, что большинство доноров готовы отдать свою почку только близкому родственнику{38}. Когда в Великобритании в 2004 году вступил в действие Закон о тканях человека, люди получили возможность законным образом отдавать почки не только родственникам.

Очень серьезную проблему представляет поиск подходящих пар доноров и реципиентов, потому что даже в тех случаях, когда имеется донор, тип его тканей и крови может не совпасть с типом тканей и крови предполагаемого реципиента. Представьте себе, что дядюшка Фред нуждается в почке, а его сын Уильям готов пожертвовать свою, но не хочет делиться почкой с чужим человеком. К несчастью, у почки Уильяма не тот тип ткани. До 2004 года на этом все кончалось, и Фред был обречен на частые сеансы диализа на специальном аппарате. Такой же была судьба многих других потенциальных реципиентов, у которых тип ткани совпадает с типом ткани Уильяма. Теперь представьте, что Джон Смит, не состоящий в родстве с Фредом и Уильямом, сталкивается с той же проблемой: его сестра Эмили нуждается в новой почке и он готов отдать ей свою, но, опять же, не готов делиться почкой с чужим человеком. И у него тип ткани отличается от типа ткани Эмили. В итоге никто не получает почку для пересадки.

Предположим, однако, что типы тканей у Джона и у Фреда, а также у Уильяма и Эмили совпадают. После 2004 года это создает условия для законного обмена почками. Задействованные в операциях хирурги могут встретиться и предложить, чтобы Джон разрешил передать его почку Фреду при условии, что почка Уильяма достанется Эмили. Оба донора с гораздо большей вероятностью согласятся на такие условия, поскольку их родственники получат новую почку, а они пожертвуют свою, иначе говоря, сделают то, что собирались сделать с самого начала. Кто именно получит чью почку, не слишком волнует ни доноров, ни реципиентов, хотя это принципиально важно с точки зрения совместимости тканей.

При современных средствах коммуникации хирурги могут обнаружить подобное совпадение, если будут вести реестр потенциальных доноров и реципиентов с указанием типа их ткани. Если число реципиентов и потенциальных доноров невелико, вероятность такого обмена также невелика, но она становится гораздо больше, когда их число растет. Число потенциальных реципиентов весьма велико: в 2017 году в Великобритании в списке ожидающих пересадку почки значилось более 5000 человек. Почка при этом могла поступить как от умершего донора, так и от живого, но число доноров меньше числа реципиентов – около 2000 на тот же момент времени. В результате среднее время ожидания превышает два года для взрослого и девять месяцев для ребенка.

Один из способов улучшить ситуацию – организация более сложных цепочек обмена почками. Закон в настоящее время разрешает сделать и это. Предположим, что Амелия, Бернард, Кэрол и Дейдра нуждаются в пересадке почки. У всех у них есть на примете доноры, изначально готовые поделиться с ними, причем только с ними. Предположим, что их доноров зовут Альберт, Берил, Карл и Дайана. Цепочка начинается с донора-альтруиста Зои, готовой отдать свою почку кому угодно. Предположим, что типы тканей допускают цепочку следующего вида:

В целом всех все устраивает. Амелия, Бернард, Кэрол и Дейдра получают новую почку. Альберт, Берил, Карл и Дайана жертвуют свою почку, хотя и не родственнику, но в рамках цепочки, которая принесет ему пользу. Часто доноров это вполне устраивает, что и делает подобные обмены возможными – ведь, если они не согласятся, их родственник не получит почку в этот раз. Зои рада, что ее альтруистический порыв принесет кому-то пользу, и ей все равно, кому именно. В данном случае – Амелии. Наконец, лишняя почка поступает в список ожидания, а это всегда полезно.

Если бы вместо этого Зои просто пожертвовала почку в список ожидания, единственное, что могли бы сделать Амелия, Бернард, Кэрол и Дейдра, – это записаться в список ожидания. Не сделав этого, они высвобождают четыре дополнительные почки. Это называется цепочкой последовательной уступки по принципу домино. Зои роняет первую костяшку, и вслед за ней падает еще несколько. Назовем этот принцип просто цепочкой.

Главное здесь, конечно, не имена, а типы тканей. Альберт – это кто угодно с тем же типом ткани, что у Зои. Берил – это кто угодно с тем же типом ткани, что у донора Альберта; Карл – это кто угодно с тем же типом ткани, что у донора Берил, и т. д. При разумном числе реципиентов и доноров подобные цепочки обычны, и хирурги могут их заметить. Однако это требует времени, даже если поиском цепочек занимается специальный человек, а каждая почка драгоценна, поэтому имеет смысл выбирать цепочки наилучшим возможным способом. Это сложно, поскольку одновременно может существовать несколько потенциальных цепочек. В таком случае хирурги могут начать работу одновременно, если только в их цепочки не входит один и тот же донор, на почку которого будут претендовать два человека. В этой ситуации одна из цепочек рвется.

Оптимизировать выбор цепочек… Это звучит математически. Если вы сможете сформулировать задачу математически и применить подходящие методы, то, возможно, сумеете и решить ее. Более того, решение не обязано быть идеальным. Оно может быть всего лишь лучше, чем результат, полученный вручную. Дэвид Мэнлав нашел способ превратить задачу об обмене почками в вопрос о графах. Теорема Эйлера здесь не помощница, но роль Эйлера неоценима, поскольку он открыл в математике новую область. За прошедшие годы математики развили тему и нашли в теории графов множество новых методов. Поскольку граф – объект дискретный, «на самом деле» всего лишь список вершин, ребер и информации о том, какое ребро соединяет какие вершины, графы замечательно подходят для компьютерной обработки. Разработаны мощные алгоритмы для анализа графов и извлечения из них полезной структуры. В их числе есть и алгоритмы, которые могут отыскивать оптимальные способы распределения доноров по пациентам для графов приемлемых размеров. Эти методы, реализованные на компьютере, применяются сегодня в Великобритании на повседневной основе.

Два типа обмена

Совместимые пары доноров и реципиентов просто обмениваются почками. Для этого нужно, чтобы два хирурга оперировали одновременно, каждый своего пациента. Так что мы, пытаясь собрать цепочки, можем не обращать внимания на совместимые пары и сосредоточиться только на несовместимых. Эти пары составляют вершины графа.

Предположим, например, что Альберт готов отдать свою почку Амелии, но совместим при этом с Бернардом. Эта ситуация показана на рисунке слева. Я ставлю имя донора вверху, а имя несовместимого с ним родственника – внизу. Стрелка означает, что «донор в ее хвосте совместим с реципиентом на острие». Этот рисунок представляет собой особый тип графа, в котором ребра имеют конкретную направленность. В отличие от мостов Кёнигсберга, эти ребра односторонние: математики называют их направленными, а получившийся граф – ориентированным или, короче, орграфом. На рисунке направленные ребра обозначены стрелками.

Если Берил совместима с Амелией, то правила предписывают нам нарисовать еще одну стрелку в обратном направлении. Таким образом создается двусторонняя связь, как на рисунке справа. Этот рисунок иллюстрирует простейший вариант обмена почками, который специалисты по теории графов называют циклом длины 2. Хирурги могут предложить Альберту пожертвовал свою почку Бернарду с условием, что Берил отдаст свою Амелии. Если все стороны согласны, то Амелия и Бернард получают по новой почке, тогда как Альберт и Берил по одной почке отдают. Хотя это и не родственная пересадка, реципиенты все-таки получают почку, так что большинство потенциальных доноров принимают обмен такого рода.

Цикл обмена почками длины 3

Следующий, более сложный тип обмена – цикл длины 3. Здесь присутствует третья пара с донором Карлом и реципиентом Кэрол. Предположим, что

Тогда хирурги могут предложить, чтобы почка Альберта досталась Бернарду, почка Берил – Кэрол, а почка Карла – Амелии. Это опять приемлемый вариант для большинства доноров.

С донорами-альтруистами вроде Зои работать приходится немного иначе, потому что они изначально ни с кем не связаны и у них нет пары. И здесь на сцену выходит небольшой математический фокус. Мы формируем соответствующую вершину графа, поставив в пару к Зои загадочного неизвестного реципиента, обозначив его подписью «кто угодно», и считаем этого реципиента совместимым с любым из наших неальтруистических доноров. На практике этот псевдореципиент представляет всех стоящих в списке ожидания при условии, что каждый из них совместим с кем-то из неальтруистических доноров. Это вполне реально, поскольку список ожидания велик. Теперь мы проводим стрелку от

к любой вершине, реципиент которой совместим с Зои. Для последовательной цепочки домино, описанной выше, получаем орграф на рисунке ниже.

Подобные цепочки непрактичны: для реализации данного варианта потребовалось бы 10 одновременно оперирующих хирургов. Операции должны проводиться одновременно, иначе, скажем, как только Кэрол получит почку от Берил, Карл может передумать и отказаться отдавать свою почку Дейдре. Люди не всегда выполняют свои обещания, если теряется выгода, даже после подписания необходимых юридических документов. При желании всегда можно найти предлог. Сказаться больным или еще что-нибудь. Сломать ногу.

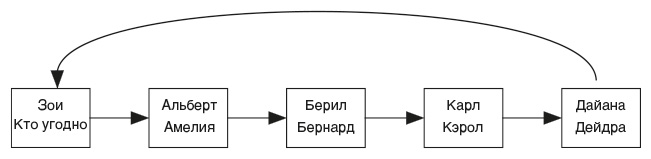
Эта цепочка слишком длинная, чтобы быть практичной

По этой причине обмены в настоящее время законодательно ограничиваются четырьмя сценариями: это циклы длины 2 и 3, которые мы уже видели, и соответствующие им циклы с участием донора-альтруиста, которые называются короткими и длинными цепочками. В короткой цепочке были бы задействованы только Зои, Альберт, Амелия и кто-то из списка ожидания. В длинную цепочку были бы включены еще Берил и Бернард. Под обменом понимается любой из этих четырех сценариев.

Обратите внимание на небольшое лукавство. Я показал эту цепочку как цикл с пятью вершинами. При реализации обмена это не совсем так, потому что у Зои нет конкретного реципиента. Зои готова уступить свою почку любому, и в конце цепочки Дайана действительно отдает почку любому (то есть списку ожидания в целом). Но на самом деле «кто угодно», кому уступает почку Зои, оказывается Амелией, и это не тот же самый человек, кому жертвует в конечном итоге последний в цепочке – Дайана. С этим помогает разобраться математика, потому что в каждом случае мы определяем занимающего позицию «кто угодно» из структуры орграфа.

Орграф обмена почками, использовавшийся в июле 2015 года, и оптимальное решение (показано сплошными черными линиями). Белые точки – доноры и реципиенты, не имеющие пары, серые точки – доноры-альтруисты, черные точки – доноры и реципиенты, получившие пару[5]

В приведенных выше орграфах отдельные циклы и цепочки показаны при помощи небольшого числа вершин и стрелок. В реальности пар много, доноров-альтруистов заметно меньше, а вот стрелок просто громадное количество. Это происходит потому, что орграф должен иметь стрелку между двумя любыми вершинами X и Y, где донор X совместим с реципиентом Y. Один и тот же донор может быть совместим со множеством реципиентов. Например, в октябре 2017 года было зарегистрировано 226 неальтруистических пар и 9 доноров-альтруистов, между которыми было проведено в совокупности 5964 стрелки. Рисунок иллюстрирует сложность структуры на другую дату. Математическая задача состоит в том, чтобы найти в этом орграфе не просто один обмен, а наилучшее возможное подмножество обменов.

Чтобы решить эту задачу математически, необходимо точно определить понятие «наилучший возможный». Это не просто множество обменов, при котором задействовано максимальное число людей. Есть и другие соображения, такие как стоимость и вероятный процент успеха. Здесь в дело вступают медицинская консультация и опыт. Служба переливания крови и трансплантации Министерства здравоохранения Великобритании (NHSBT) разработала стандартную систему количественной оценки пользы от каждой пересадки органа. Во внимание принимаются такие факторы, как срок ожидания пациента в очереди, уровни несовместимости по типу тканей и разница в возрасте между донором и реципиентом. При помощи статистического анализа эти факторы собираются в единую числовую оценку – действительное число, которое называют весом. Вес вычисляется для каждой стрелки на орграфе, то есть для каждой потенциальной пересадки.

Имеется одно очевидное условие: одна и та же вершина графа не может быть задействована в двух цепочках, поскольку невозможно отдать одну и ту же почку двум людям. Математически это равноценно утверждению, что циклы, составляющие множество, не пересекаются. Остальные условия тоньше. Некоторые циклы длины 3 имеют дополнительную полезную черту: лишнюю стрелку в обратном направлении между двумя вершинами. На рисунке показан случай, когда, помимо стрелок предыдущего цикла длины 3, в цикле имеется еще одна от пары Берил к паре Амелии. Это означает, что Берил совместима не только с Кэрол, но и с Амелией. Если где-то на поздней стадии Карл вдруг выпадет из договоренности по обмену, то Кэрол тоже можно исключить; останется цикл длины 2, в котором Альберт передает почку Бернарду, а Берил – Амелии, и этот обмен по-прежнему может быть реализован. Математически эти три вершины образуют цикл длины 3, и дополнительно две из его вершин образуют цикл длины 2. Подобная дополнительная стрелка называется обратной дугой. Любой цикл длины 3 с обратной дугой и циклом длины 2 называется эффективным циклом длины 2.

Согласно определению Консультативной группы по почкам при NHSBT, множество обменов почками является оптимальным, если оно:

(1) максимизирует число эффективных циклов длины 2;

(2) содержит как можно больше циклов, при выполнении условия (1);

(3) использует как можно меньше циклов длины 3, при выполнении условий (1) и (2);

(4) максимизирует число обратных дуг, при выполнении условий (1)–(3);

(5) максимизирует суммарный вес всех циклов, при выполнении условий (1)–(4).

Эффективный цикл длины 2

Интуитивно понятно, что это определение отдает приоритет определенным моментам, а когда выполнено главное условие, в дело последовательно вступают остальные, с более низким приоритетом. Например, условие (1) гарантирует, что включение в схему трехсторонних обменов не уменьшит число двухсторонних обменов, которые могли бы быть сделаны. Такой подход обеспечивает, во-первых, простоту, а во-вторых – возможность продолжать с циклом длины 2, если кто-то вдруг выпадет из схемы. Условие (5) означает, что множество обменов должно быть как можно более эффективным и иметь максимальную вероятность успеха, но начинать думать об этом можно только после того, как приняты главные решения по пунктам (1)–(4).

Математическая задача состоит в том, чтобы найти оптимальное множество обменов, соответствующее данным критериям. Если немного подумать и прикинуть цифры, несложно понять, что проверить все возможные множества обменов нереально. Их попросту слишком много. Допустим, у нас имеется 250 вершин и 5000 ребер. В среднем с каждой вершиной связано 20 ребер, и для упрощения оценки будем считать, что 10 из них в эту вершину входят, а 10 – выходят. Предположим, мы хотим найти все возможные циклы длины 2. Выберем какую-нибудь вершину и пройдем вдоль 10 выходящих из нее стрелочек. Каждая стрелочка заканчивается у другой вершины, из которой тоже выходит 10 стрелочек. Мы получаем цикл длины 2, если конечная вершина после этого совпадет с начальной. Получаем 100 вариантов для проверки. Для нахождения цикла длины 3 необходимо проверить 100 × 10 = 1000 вариантов, а это означает 1100 проверок на каждую вершину. Вершин у нас 250, то есть проверять нужно 275 000 вариантов, если не учитывать упрощения, которые, конечно, могут снизить число проверок, но не изменят общего порядка величины.

Однако, даже если все получилось, вам на данный момент удалось всего лишь составить список возможных циклов длины 2 и 3. Обмен – это множество циклов, и число множеств растет экспоненциально с ростом числа циклов. В октябре 2017 года в орграфе были 381 цикл длины 2 и 3815 циклов длины 3. Число наборов из одних только циклов длины 2 составляет 2³⁸¹, а это число с 115 знаками. Число наборов из циклов длины 3 имеет 1149 знаков. А мы еще даже не проверили, какие из множеств не имеют пересечений.

Вряд ли стоит пояснять, что на самом деле эту задачу решают не так. Но из приведенных данных понятно, что для этого необходимо придумать какие-то достаточно эффективные методы. Я лишь набросаю некоторые из задействованных в решении идей. Вообще, все это можно рассматривать как разновидность пресловутой задачи коммивояжера: как задачу комбинаторной оптимизации с другими, конечно, ограничениями, но аналогичными рассуждениями. Принципиально важно, сколько времени требуется на поиск оптимального решения. Эту стратегию можно исследовать с точки зрения вычислительной сложности, как в главе 3.

Если в схеме участвуют только циклы длины 2, то оптимальное множество обменов может быть вычислено за полиномиальное время, класс сложности P, с использованием стандартных методов построения паросочетаний с максимальным весом в графе. Если присутствуют и циклы длины 3, даже без доноров-альтруистов, задача оптимизации становится NP-трудной. Тем не менее Мэнлав с коллегами разработал работоспособный алгоритм на базе линейного программирования, о котором мы говорили в главе 3. Их алгоритм UKLKSS перестраивает задачу оптимизации так, чтобы ее можно решить при помощи последовательности вычислений по методу линейного программирования. Результат каждого расчета подается на вход следующего как дополнительное ограничение. Так что условие (1) оптимизируется; при этом используется метод, известный как алгоритм Эдмондса в реализации Сильвио Микали и Виджая Вазирани. Алгоритм Эдмондса находит максимальное покрытие в графе за время, пропорциональное числу ребер, умноженному на квадратный корень из числа вершин. Покрытие связывает пары вершин на концах общего ребра, и задача в том, чтобы покрыть как можно большее число пар вершин без использования двух ребер, которые имеют одну общую вершину.

После того как оптимизация по условию (1) проведена, полученное решение оптимизируется по условию (2) с использованием алгоритма, известного как целочисленный программный решатель COIN-Cbc, части библиотеки алгоритмов проекта Вычислительной инфраструктуры для исследования операций, и т. д.

К концу 2017 года при помощи этих методов теории графов было найдено 1278 потенциальных вариантов пересадки, но реализовали только 760 из них, потому что на последних этапах оценки вылезают разные проблемы: выясняется, например, что типы тканей не так хорошо совместимы, как считалось ранее, или что доноры или реципиенты по состоянию здоровья не могут выдержать операции. Однако систематическое использование алгоритмов из теории графов для эффективной организации пересадки почек – серьезный шаг вперед по сравнению с прежними методами. Кроме того, это указывает нам путь к дальнейшим усовершенствованиям, поскольку сегодня мы можем хранить почки вне тела дольше, так что все операции в цепочке не обязательно проводить в один день. Теперь можно задуматься и о более длинных цепочках, а это ставит перед нами новые математические задачи.

Я не пытаюсь утверждать, что Эйлер умел предвидеть будущее. Он, конечно, не думал, что его остроумное решение глупой головоломки когда-нибудь пригодится в медицине. И уж точно он не мог предположить, что оно найдет применение в трансплантологии – ведь в те времена хирургия не слишком отличалась от ремесла мясников. Но я хочу отдать ему должное – даже в те далекие дни он видел, что эта головоломка намекает математикам на нечто более глубокое, и прямо говорил об этом. Взгляните на эпиграф к этой главе. Эйлер неоднократно упоминает «геометрию положения» в контексте данной задачи. Это понятие он обозначает на латыни как analysis situs и отдает Лейбницу честь изобретения термина и, косвенно, осознания того, что такой предмет может оказаться важен. Самого Эйлера, очевидно, заинтриговала идея геометрии, имеющей дело не с традиционными евклидовыми фигурами. Он не отвергает эту идею из-за ее неортодоксальности, совсем наоборот. Ему приятно внести свой вклад в развитие такой геометрии. Он развлекается.

Мечта Лейбница осуществилась в XX веке после весьма существенных достижений XIX века. Мы сегодня называем эту область математики топологией, и в главе 13 я покажу некоторые ее новые применения. Теория графов по-прежнему не теряет связи с топологией, но их развитие шло разными путями. Такие понятия, как вес ребра, имеют численный, а не топологический характер. Но идея о том, что графы можно использовать для моделирования сложных взаимодействующих систем и решения задач оптимизации, восходит к Эйлеру. Он занялся вопросами нового типа потому, что они захватили его воображение, и придумал собственные способы поиска ответов на них. Произошло это в Санкт-Петербурге, в России, куда он приехал по приглашению недавно созданной Академии наук почти три столетия назад. Всякий, кому пересаживают почку, будь то в Великобритании или в любой другой стране, где пользуются методами теории графов для более эффективного распределения органов, должен восхищаться тем, что сделал Эйлер.